Fast and Scalable Estimator for Sparse and Unit-Rank Higher-Order Regression Models
Paper and Code
Nov 29, 2019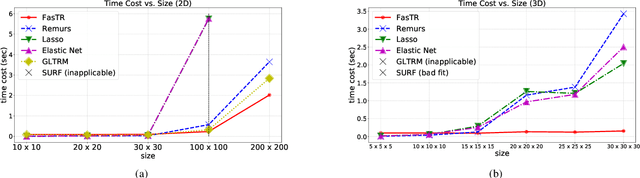
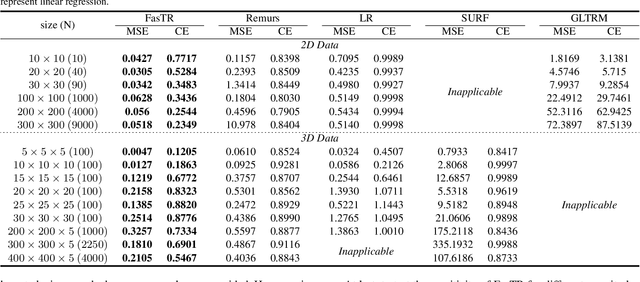
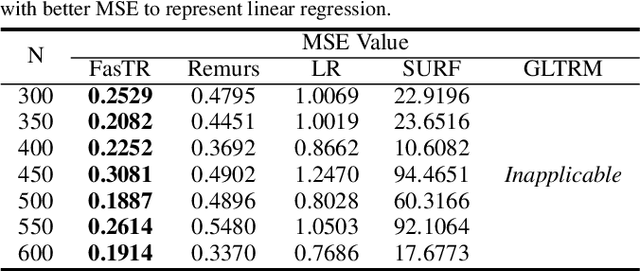
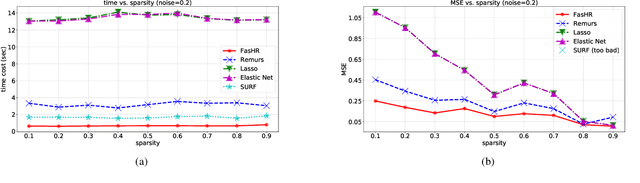
Because tensor data appear more and more frequently in various scientific researches and real-world applications, analyzing the relationship between tensor features and the univariate outcome becomes an elementary task in many fields. To solve this task, we propose \underline{Fa}st \underline{S}parse \underline{T}ensor \underline{R}egression model (FasTR) based on so-called unit-rank CANDECOMP/PARAFAC decomposition. FasTR first decomposes the tensor coefficient into component vectors and then estimates each vector with $\ell_1$ regularized regression. Because of the independence of component vectors, FasTR is able to solve in a parallel way and the time complexity is proved to be superior to previous models. We evaluate the performance of FasTR on several simulated datasets and a real-world fMRI dataset. Experiment results show that, compared with four baseline models, in every case, FasTR can compute a better solution within less time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge