Sparse and Low-Rank Tensor Regression via Parallel Proximal Method

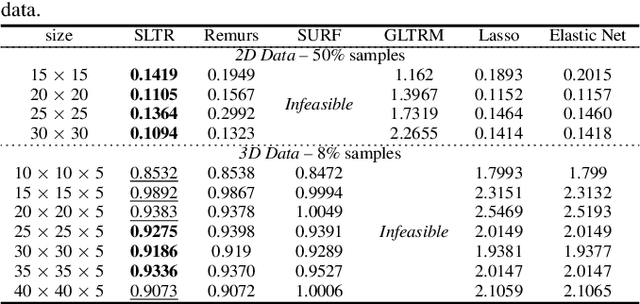
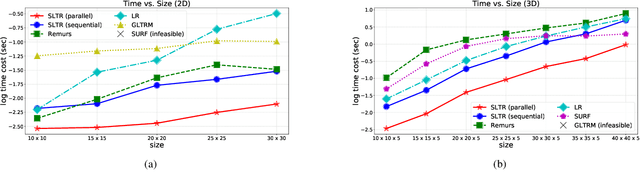
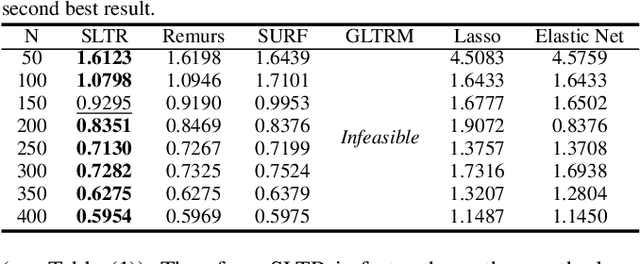
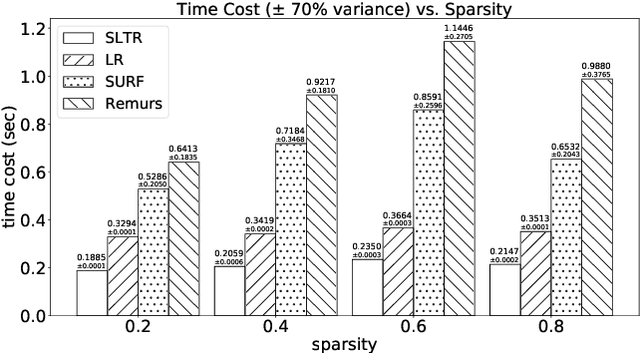
Motivated by applications in various scientific fields having demand of predicting relationship between higher-order (tensor) feature and univariate response, we propose a \underline{S}parse and \underline{L}ow-rank \underline{T}ensor \underline{R}egression model (SLTR). This model enforces sparsity and low-rankness of the tensor coefficient by directly applying $\ell_1$ norm and tensor nuclear norm on it respectively, such that (1) the structural information of tensor is preserved and (2) the data interpretation is convenient. To make the solving procedure scalable and efficient, SLTR makes use of the proximal gradient method to optimize two norm regularizers, which can be easily implemented parallelly. Additionally, a tighter convergence rate is proved over three-order tensor data. We evaluate SLTR on several simulated datasets and one fMRI dataset. Experiment results show that, compared with previous models, SLTR is able to obtain a solution no worse than others with much less time cost.