A Fast and Scalable Joint Estimator for Learning Multiple Related Sparse Gaussian Graphical Models
Paper and Code
Mar 20, 2018
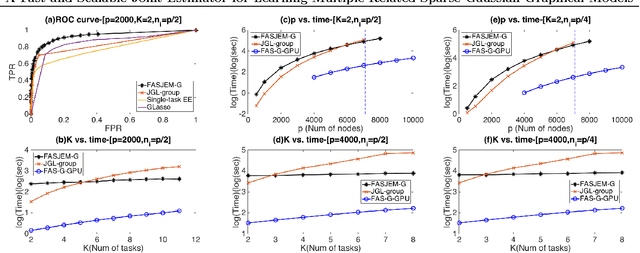

Estimating multiple sparse Gaussian Graphical Models (sGGMs) jointly for many related tasks (large $K$) under a high-dimensional (large $p$) situation is an important task. Most previous studies for the joint estimation of multiple sGGMs rely on penalized log-likelihood estimators that involve expensive and difficult non-smooth optimizations. We propose a novel approach, FASJEM for \underline{fa}st and \underline{s}calable \underline{j}oint structure-\underline{e}stimation of \underline{m}ultiple sGGMs at a large scale. As the first study of joint sGGM using the Elementary Estimator framework, our work has three major contributions: (1) We solve FASJEM through an entry-wise manner which is parallelizable. (2) We choose a proximal algorithm to optimize FASJEM. This improves the computational efficiency from $O(Kp^3)$ to $O(Kp^2)$ and reduces the memory requirement from $O(Kp^2)$ to $O(K)$. (3) We theoretically prove that FASJEM achieves a consistent estimation with a convergence rate of $O(\log(Kp)/n_{tot})$. On several synthetic and four real-world datasets, FASJEM shows significant improvements over baselines on accuracy, computational complexity, and memory costs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge