Learning in complex action spaces without policy gradients

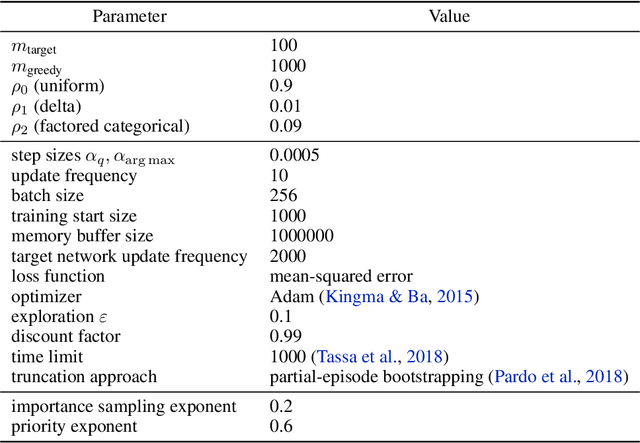
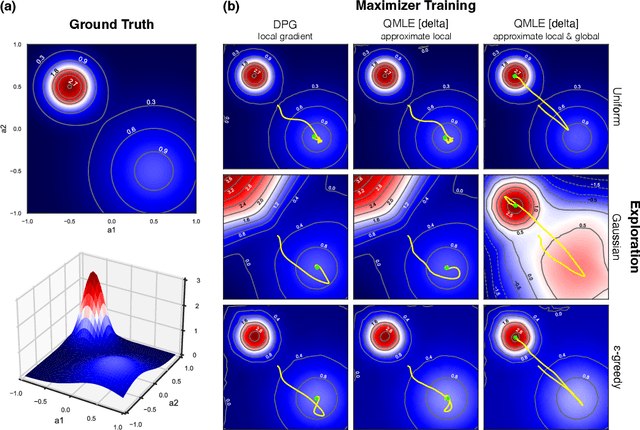
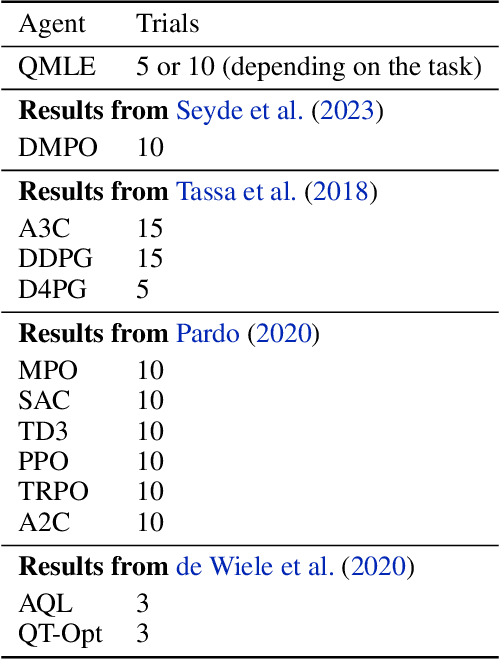
Conventional wisdom suggests that policy gradient methods are better suited to complex action spaces than action-value methods. However, foundational studies have shown equivalences between these paradigms in small and finite action spaces (O'Donoghue et al., 2017; Schulman et al., 2017a). This raises the question of why their computational applicability and performance diverge as the complexity of the action space increases. We hypothesize that the apparent superiority of policy gradients in such settings stems not from intrinsic qualities of the paradigm, but from universal principles that can also be applied to action-value methods to serve similar functionality. We identify three such principles and provide a framework for incorporating them into action-value methods. To support our hypothesis, we instantiate this framework in what we term QMLE, for Q-learning with maximum likelihood estimation. Our results show that QMLE can be applied to complex action spaces with a controllable computational cost that is comparable to that of policy gradient methods, all without using policy gradients. Furthermore, QMLE demonstrates strong performance on the DeepMind Control Suite, even when compared to the state-of-the-art methods such as DMPO and D4PG.

On the Pitfalls of Heteroscedastic Uncertainty Estimation with Probabilistic Neural Networks

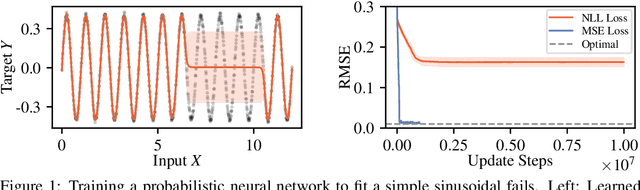
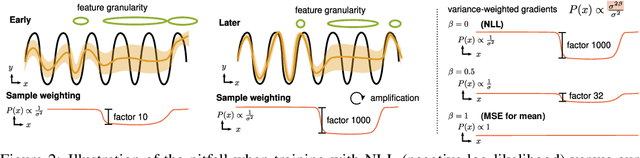
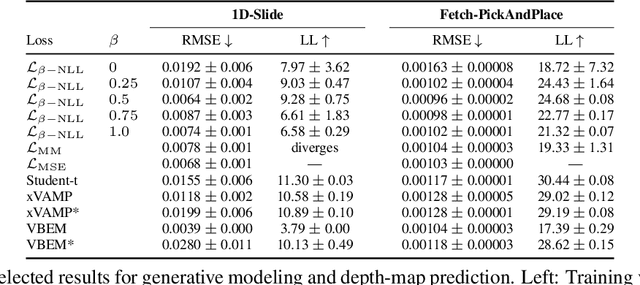
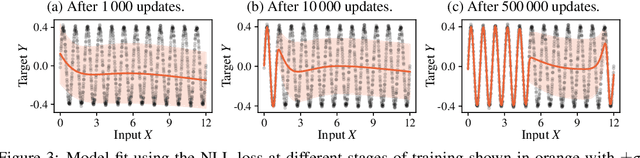
Capturing aleatoric uncertainty is a critical part of many machine learning systems. In deep learning, a common approach to this end is to train a neural network to estimate the parameters of a heteroscedastic Gaussian distribution by maximizing the logarithm of the likelihood function under the observed data. In this work, we examine this approach and identify potential hazards associated with the use of log-likelihood in conjunction with gradient-based optimizers. First, we present a synthetic example illustrating how this approach can lead to very poor but stable parameter estimates. Second, we identify the culprit to be the log-likelihood loss, along with certain conditions that exacerbate the issue. Third, we present an alternative formulation, termed $\beta$-NLL, in which each data point's contribution to the loss is weighted by the $\beta$-exponentiated variance estimate. We show that using an appropriate $\beta$ largely mitigates the issue in our illustrative example. Fourth, we evaluate this approach on a range of domains and tasks and show that it achieves considerable improvements and performs more robustly concerning hyperparameters, both in predictive RMSE and log-likelihood criteria.

Orchestrated Value Mapping for Reinforcement Learning

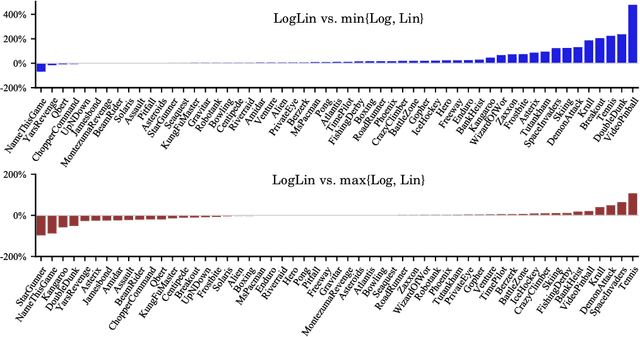
We present a general convergent class of reinforcement learning algorithms that is founded on two distinct principles: (1) mapping value estimates to a different space using arbitrary functions from a broad class, and (2) linearly decomposing the reward signal into multiple channels. The first principle enables incorporating specific properties into the value estimator that can enhance learning. The second principle, on the other hand, allows for the value function to be represented as a composition of multiple utility functions. This can be leveraged for various purposes, e.g. dealing with highly varying reward scales, incorporating a priori knowledge about the sources of reward, and ensemble learning. Combining the two principles yields a general blueprint for instantiating convergent algorithms by orchestrating diverse mapping functions over multiple reward channels. This blueprint generalizes and subsumes algorithms such as Q-Learning, Log Q-Learning, and Q-Decomposition. In addition, our convergence proof for this general class relaxes certain required assumptions in some of these algorithms. Based on our theory, we discuss several interesting configurations as special cases. Finally, to illustrate the potential of the design space that our theory opens up, we instantiate a particular algorithm and evaluate its performance on the Atari suite.

Learning to Represent Action Values as a Hypergraph on the Action Vertices

Action-value estimation is a critical component of many reinforcement learning (RL) methods whereby sample complexity relies heavily on how fast a good estimator for action value can be learned. By viewing this problem through the lens of representation learning, good representations of both state and action can facilitate action-value estimation. While advances in deep learning have seamlessly driven progress in learning state representations, given the specificity of the notion of agency to RL, little attention has been paid to learning action representations. We conjecture that leveraging the combinatorial structure of multi-dimensional action spaces is a key ingredient for learning good representations of action. To test this, we set forth the action hypergraph networks framework---a class of functions for learning action representations with a relational inductive bias. Using this framework we realise an agent class based on a combination with deep Q-networks, which we dub hypergraph Q-networks. We show the effectiveness of our approach on a myriad of domains: illustrative prediction problems under minimal confounding effects, Atari 2600 games, and physical control benchmarks.

A neural network oracle for quantum nonlocality problems in networks

Characterizing quantum nonlocality in networks is a challenging problem. A key point is to devise methods for deciding whether an observed probability distribution achievable via quantum resources could also be reproduced using classical resources. The task is challenging even for simple networks, both analytically and using standard numerical techniques. We propose to use neural networks as numerical tools to overcome these challenges, by learning the classical strategies required to reproduce a distribution. As such, the neural network acts as an oracle, demonstrating that a behavior is classical if it can be learned. We apply our method to several examples in the triangle configuration. After demonstrating that the method is consistent with previously known results, we show that the distribution presented in [N. Gisin, Entropy 21(3), 325 (2019)] is indeed nonlocal as conjectured. Furthermore the method allows us to get an estimate on its noise robustness.

Using a Logarithmic Mapping to Enable Lower Discount Factors in Reinforcement Learning

In an effort to better understand the different ways in which the discount factor affects the optimization process in reinforcement learning, we designed a set of experiments to study each effect in isolation. Our analysis reveals that the common perception that poor performance of low discount factors is caused by (too) small action-gaps requires revision. We propose an alternative hypothesis, which identifies the size-difference of the action-gap across the state-space as the primary cause. We then introduce a new method that enables more homogeneous action-gaps by mapping value estimates to a logarithmic space. We prove convergence for this method under standard assumptions and demonstrate empirically that it indeed enables lower discount factors for approximate reinforcement-learning methods. This in turn allows tackling a class of reinforcement-learning problems that are challenging to solve with traditional methods.

Prioritizing Starting States for Reinforcement Learning

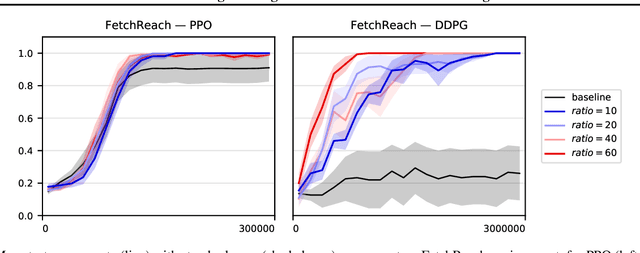
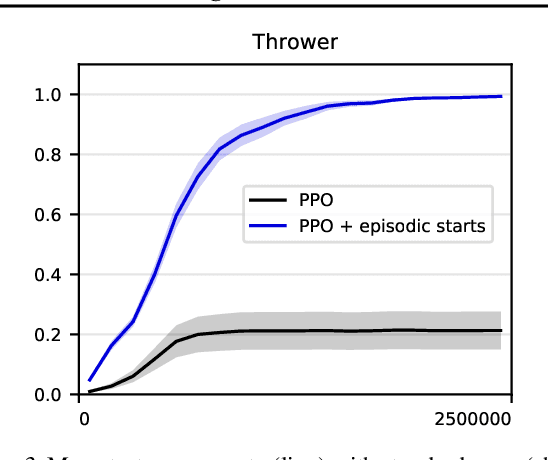
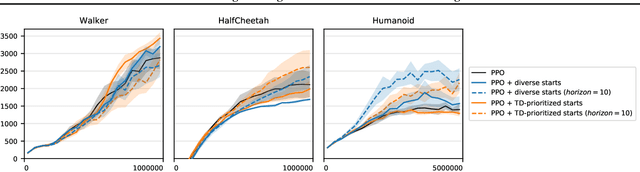
Online, off-policy reinforcement learning algorithms are able to use an experience memory to remember and replay past experiences. In prior work, this approach was used to stabilize training by breaking the temporal correlations of the updates and avoiding the rapid forgetting of possibly rare experiences. In this work, we propose a conceptually simple framework that uses an experience memory to help exploration by prioritizing the starting states from which the agent starts acting in the environment, importantly, in a fashion that is also compatible with on-policy algorithms. Given the capacity to restart the agent in states corresponding to its past observations, we achieve this objective by (i) enabling the agent to restart in states belonging to significant past experiences (e.g., nearby goals), and (ii) promoting faster coverage of the state space through starting from a more diverse set of states. While, using a good measure of priority to identify significant past transitions, we expect case (i) to more considerably help exploration in certain problems (e.g., sparse reward tasks), we hypothesize that case (ii) will generally be beneficial, even without any prioritization. We show empirically that our approach improves learning performance for both off-policy and on-policy deep reinforcement learning methods, with the most notable improvement in a significantly sparse reward task.

Time Limits in Reinforcement Learning

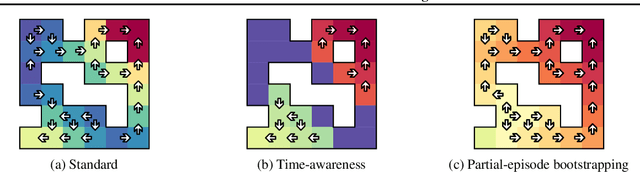
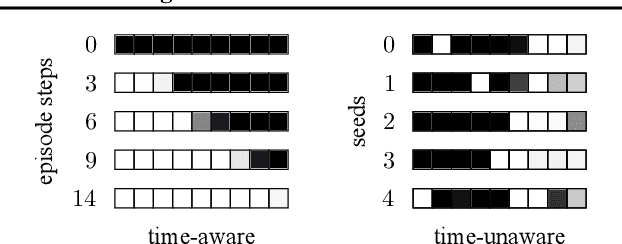
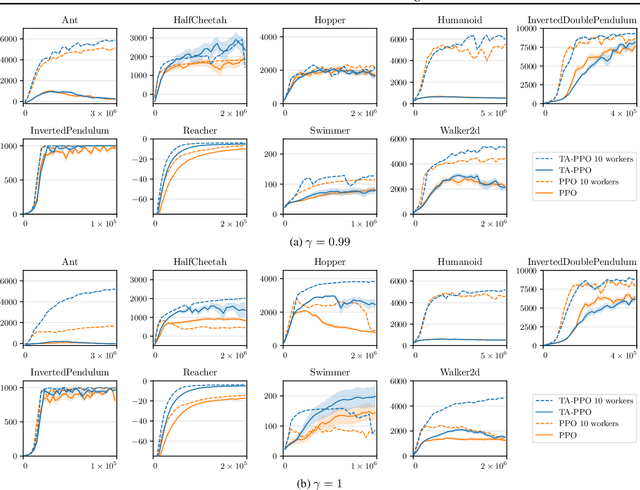
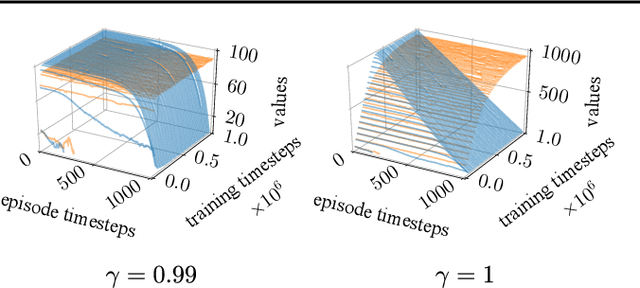
In reinforcement learning, it is common to let an agent interact for a fixed amount of time with its environment before resetting it and repeating the process in a series of episodes. The task that the agent has to learn can either be to maximize its performance over (i) that fixed period, or (ii) an indefinite period where time limits are only used during training to diversify experience. In this paper, we provide a formal account for how time limits could effectively be handled in each of the two cases and explain why not doing so can cause state-aliasing and invalidation of experience replay, leading to suboptimal policies and training instability. In case (i), we argue that the terminations due to time limits are in fact part of the environment, and thus a notion of the remaining time should be included as part of the agent's input to avoid violation of the Markov property. In case (ii), the time limits are not part of the environment and are only used to facilitate learning. We argue that this insight should be incorporated by bootstrapping from the value of the state at the end of each partial episode. For both cases, we illustrate empirically the significance of our considerations in improving the performance and stability of existing reinforcement learning algorithms, showing state-of-the-art results on several control tasks.

Action Branching Architectures for Deep Reinforcement Learning

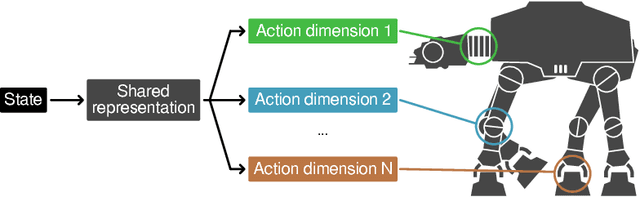
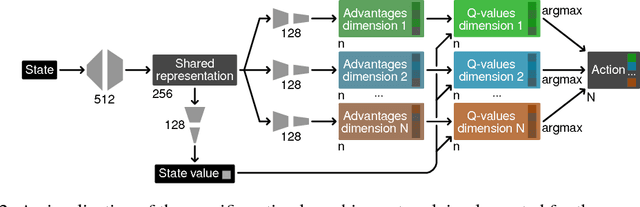
Discrete-action algorithms have been central to numerous recent successes of deep reinforcement learning. However, applying these algorithms to high-dimensional action tasks requires tackling the combinatorial increase of the number of possible actions with the number of action dimensions. This problem is further exacerbated for continuous-action tasks that require fine control of actions via discretization. In this paper, we propose a novel neural architecture featuring a shared decision module followed by several network branches, one for each action dimension. This approach achieves a linear increase of the number of network outputs with the number of degrees of freedom by allowing a level of independence for each individual action dimension. To illustrate the approach, we present a novel agent, called Branching Dueling Q-Network (BDQ), as a branching variant of the Dueling Double Deep Q-Network (Dueling DDQN). We evaluate the performance of our agent on a set of challenging continuous control tasks. The empirical results show that the proposed agent scales gracefully to environments with increasing action dimensionality and indicate the significance of the shared decision module in coordination of the distributed action branches. Furthermore, we show that the proposed agent performs competitively against a state-of-the-art continuous control algorithm, Deep Deterministic Policy Gradient (DDPG).

Multiplayer Games for Learning Multirobot Coordination Algorithms

Humans have an impressive ability to solve complex coordination problems in a fully distributed manner. This ability, if learned as a set of distributed multirobot coordination strategies, can enable programming large groups of robots to collaborate towards complex coordination objectives in a way similar to humans. Such strategies would offer robustness, adaptability, fault-tolerance, and, importantly, distributed decision-making. To that end, we have designed a networked gaming platform to investigate human group behavior, specifically in solving complex collaborative coordinated tasks. Through this platform, we are able to limit the communication, sensing, and actuation capabilities provided to the players. With the aim of learning coordination algorithms for robots in mind, we define these capabilities to mimic those of a simple ground robot.