Daniel Cavalcanti
Fast semidefinite programming with feedforward neural networks
Nov 12, 2020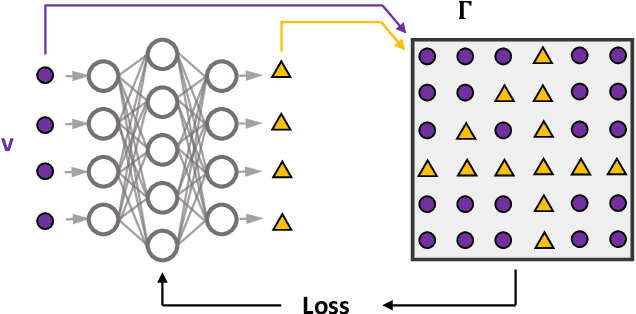
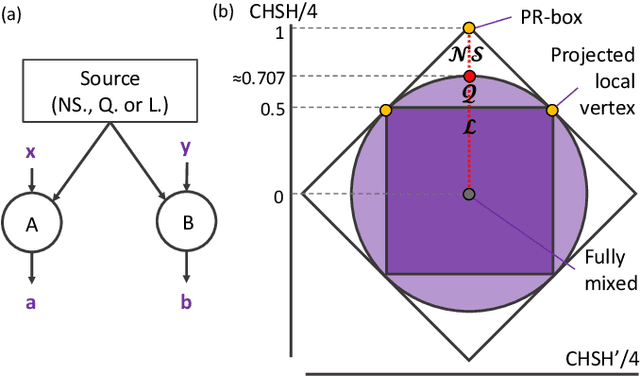
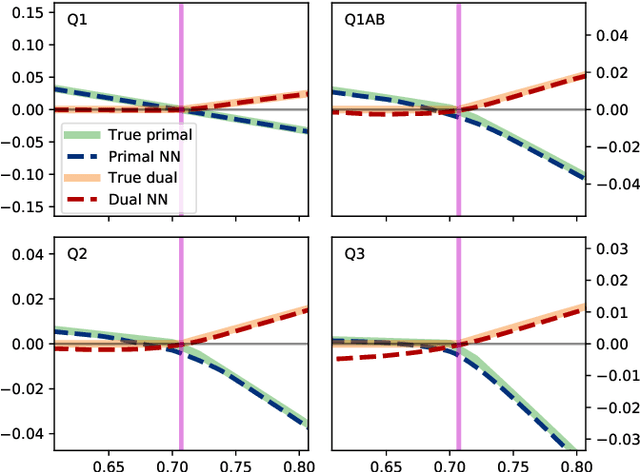
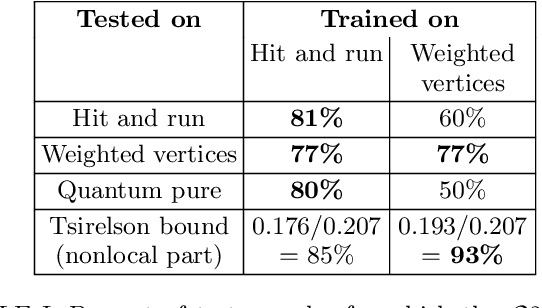
Abstract:Semidefinite programming is an important optimization task, often used in time-sensitive applications. Though they are solvable in polynomial time, in practice they can be too slow to be used in online, i.e. real-time applications. Here we propose to solve feasibility semidefinite programs using artificial neural networks. Given the optimization constraints as an input, a neural network outputs values for the optimization parameters such that the constraints are satisfied, both for the primal and the dual formulations of the task. We train the network without having to exactly solve the semidefinite program even once, thus avoiding the possibly time-consuming task of having to generate many training samples with conventional solvers. The neural network method is only inconclusive if both the primal and dual models fail to provide feasible solutions. Otherwise we always obtain a certificate, which guarantees false positives to be excluded. We examine the performance of the method on a hierarchy of quantum information tasks, the Navascu\'es-Pironio-Ac\'in hierarchy applied to the Bell scenario. We demonstrate that the trained neural network gives decent accuracy, while showing orders of magnitude increase in speed compared to a traditional solver.
A neural network oracle for quantum nonlocality problems in networks
Jul 24, 2019



Abstract:Characterizing quantum nonlocality in networks is a challenging problem. A key point is to devise methods for deciding whether an observed probability distribution achievable via quantum resources could also be reproduced using classical resources. The task is challenging even for simple networks, both analytically and using standard numerical techniques. We propose to use neural networks as numerical tools to overcome these challenges, by learning the classical strategies required to reproduce a distribution. As such, the neural network acts as an oracle, demonstrating that a behavior is classical if it can be learned. We apply our method to several examples in the triangle configuration. After demonstrating that the method is consistent with previously known results, we show that the distribution presented in [N. Gisin, Entropy 21(3), 325 (2019)] is indeed nonlocal as conjectured. Furthermore the method allows us to get an estimate on its noise robustness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge