Thermodynamic Computing via Autonomous Quantum Thermal Machines

We develop a physics-based model for classical computation based on autonomous quantum thermal machines. These machines consist of few interacting quantum bits (qubits) connected to several environments at different temperatures. Heat flows through the machine are here exploited for computing. The process starts by setting the temperatures of the environments according to the logical input. The machine evolves, eventually reaching a non-equilibrium steady state, from which the output of the computation can be determined via the temperature of an auxilliary finite-size reservoir. Such a machine, which we term a "thermodynamic neuron", can implement any linearly-separable function, and we discuss explicitly the cases of NOT, 3-majority and NOR gates. In turn, we show that a network of thermodynamic neurons can perform any desired function. We discuss the close connection between our model and artificial neurons (perceptrons), and argue that our model provides an alternative physics-based analogue implementation of neural networks, and more generally a platform for thermodynamic computing.

Building separable approximations for quantum states via neural networks

Finding the closest separable state to a given target state is a notoriously difficult task, even more difficult than deciding whether a state is entangled or separable. To tackle this task, we parametrize separable states with a neural network and train it to minimize the distance to a given target state, with respect to a differentiable distance, such as the trace distance or Hilbert-Schmidt distance. By examining the output of the algorithm, we can deduce whether the target state is entangled or not, and construct an approximation for its closest separable state. We benchmark the method on a variety of well-known classes of bipartite states and find excellent agreement, even up to local dimension of $d=10$. Moreover, we show our method to be efficient in the multipartite case, considering different notions of separability. Examining three and four-party GHZ and W states we recover known bounds and obtain novel ones, for instance for triseparability. Finally, we show how to use the neural network's results to gain analytic insight.

Fast semidefinite programming with feedforward neural networks

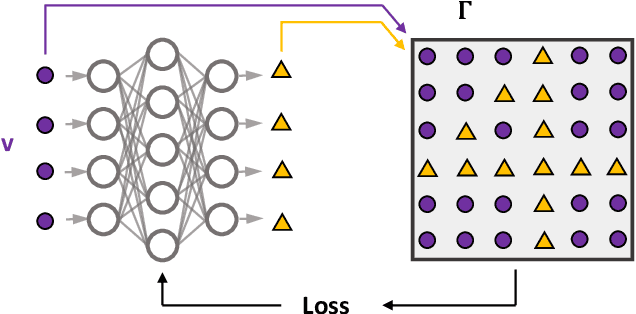
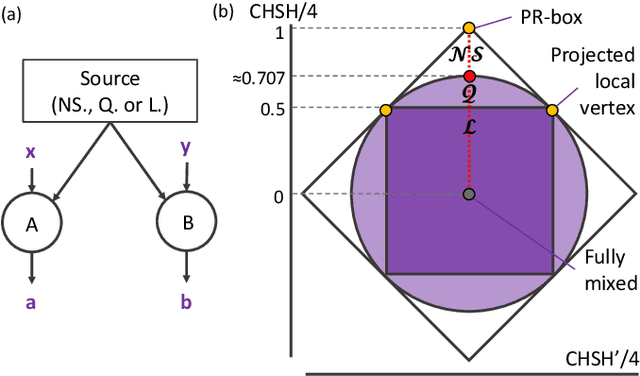
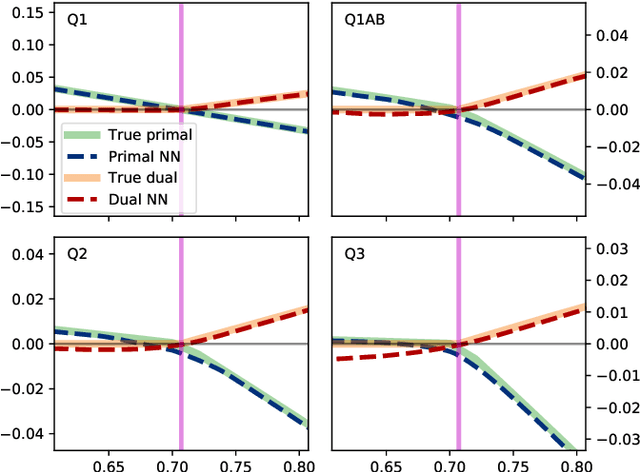
Semidefinite programming is an important optimization task, often used in time-sensitive applications. Though they are solvable in polynomial time, in practice they can be too slow to be used in online, i.e. real-time applications. Here we propose to solve feasibility semidefinite programs using artificial neural networks. Given the optimization constraints as an input, a neural network outputs values for the optimization parameters such that the constraints are satisfied, both for the primal and the dual formulations of the task. We train the network without having to exactly solve the semidefinite program even once, thus avoiding the possibly time-consuming task of having to generate many training samples with conventional solvers. The neural network method is only inconclusive if both the primal and dual models fail to provide feasible solutions. Otherwise we always obtain a certificate, which guarantees false positives to be excluded. We examine the performance of the method on a hierarchy of quantum information tasks, the Navascu\'es-Pironio-Ac\'in hierarchy applied to the Bell scenario. We demonstrate that the trained neural network gives decent accuracy, while showing orders of magnitude increase in speed compared to a traditional solver.

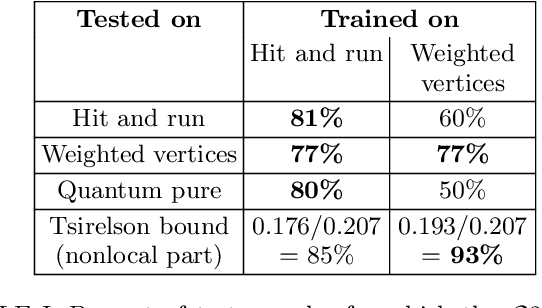
A neural network oracle for quantum nonlocality problems in networks

Characterizing quantum nonlocality in networks is a challenging problem. A key point is to devise methods for deciding whether an observed probability distribution achievable via quantum resources could also be reproduced using classical resources. The task is challenging even for simple networks, both analytically and using standard numerical techniques. We propose to use neural networks as numerical tools to overcome these challenges, by learning the classical strategies required to reproduce a distribution. As such, the neural network acts as an oracle, demonstrating that a behavior is classical if it can be learned. We apply our method to several examples in the triangle configuration. After demonstrating that the method is consistent with previously known results, we show that the distribution presented in [N. Gisin, Entropy 21(3), 325 (2019)] is indeed nonlocal as conjectured. Furthermore the method allows us to get an estimate on its noise robustness.