Fast semidefinite programming with feedforward neural networks
Paper and Code
Nov 12, 2020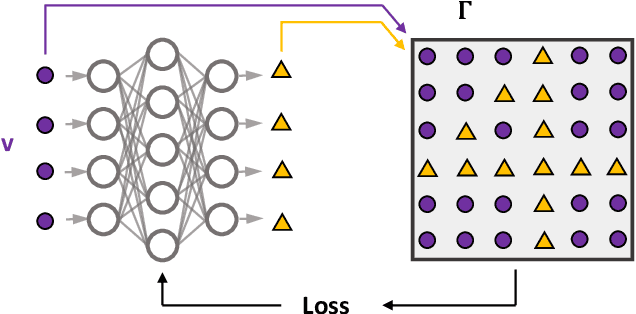
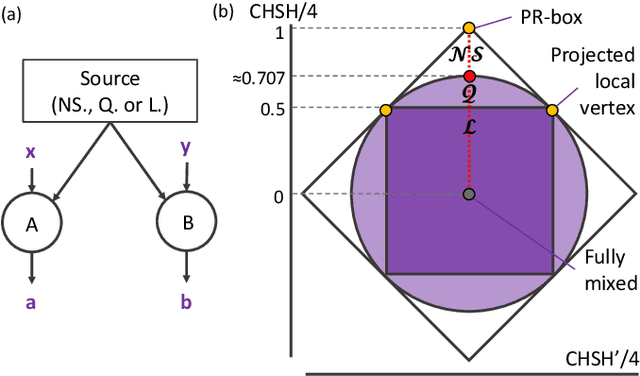
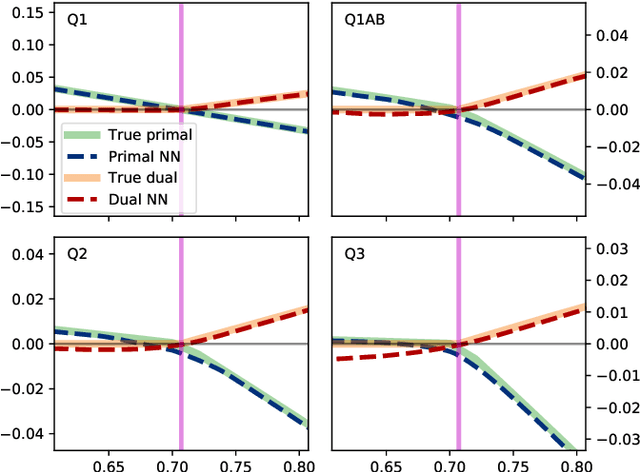
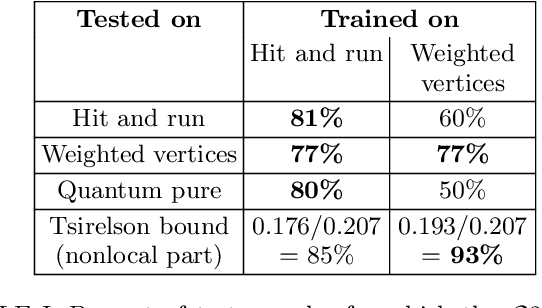
Semidefinite programming is an important optimization task, often used in time-sensitive applications. Though they are solvable in polynomial time, in practice they can be too slow to be used in online, i.e. real-time applications. Here we propose to solve feasibility semidefinite programs using artificial neural networks. Given the optimization constraints as an input, a neural network outputs values for the optimization parameters such that the constraints are satisfied, both for the primal and the dual formulations of the task. We train the network without having to exactly solve the semidefinite program even once, thus avoiding the possibly time-consuming task of having to generate many training samples with conventional solvers. The neural network method is only inconclusive if both the primal and dual models fail to provide feasible solutions. Otherwise we always obtain a certificate, which guarantees false positives to be excluded. We examine the performance of the method on a hierarchy of quantum information tasks, the Navascu\'es-Pironio-Ac\'in hierarchy applied to the Bell scenario. We demonstrate that the trained neural network gives decent accuracy, while showing orders of magnitude increase in speed compared to a traditional solver.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge