Action Branching Architectures for Deep Reinforcement Learning
Paper and Code
Nov 24, 2017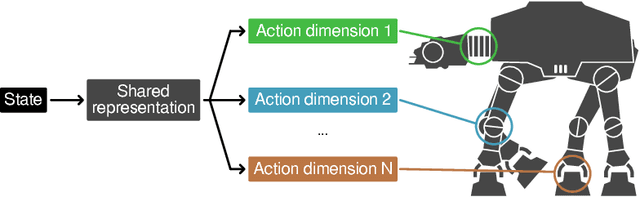

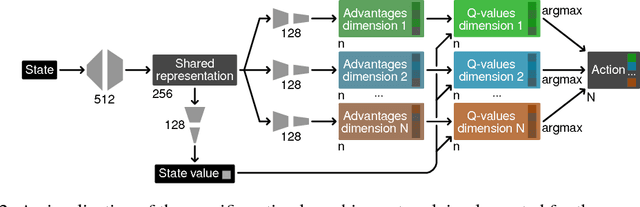
Discrete-action algorithms have been central to numerous recent successes of deep reinforcement learning. However, applying these algorithms to high-dimensional action tasks requires tackling the combinatorial increase of the number of possible actions with the number of action dimensions. This problem is further exacerbated for continuous-action tasks that require fine control of actions via discretization. In this paper, we propose a novel neural architecture featuring a shared decision module followed by several network branches, one for each action dimension. This approach achieves a linear increase of the number of network outputs with the number of degrees of freedom by allowing a level of independence for each individual action dimension. To illustrate the approach, we present a novel agent, called Branching Dueling Q-Network (BDQ), as a branching variant of the Dueling Double Deep Q-Network (Dueling DDQN). We evaluate the performance of our agent on a set of challenging continuous control tasks. The empirical results show that the proposed agent scales gracefully to environments with increasing action dimensionality and indicate the significance of the shared decision module in coordination of the distributed action branches. Furthermore, we show that the proposed agent performs competitively against a state-of-the-art continuous control algorithm, Deep Deterministic Policy Gradient (DDPG).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge