Pose-NDF: Modeling Human Pose Manifolds with Neural Distance Fields

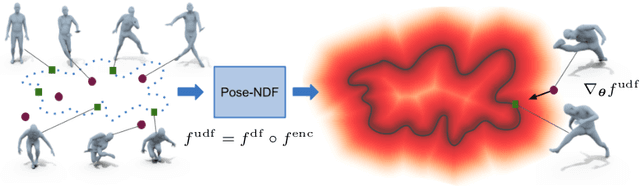
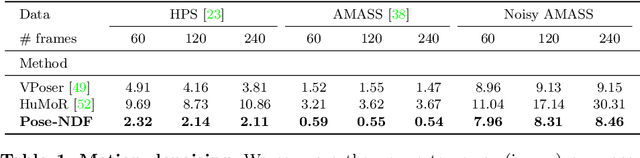
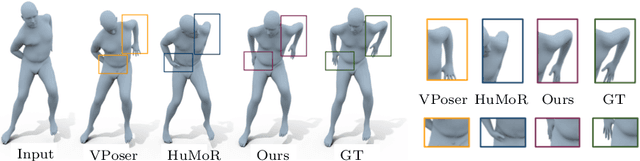
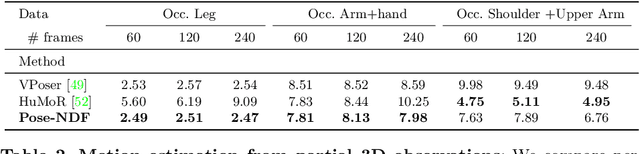
We present Pose-NDF, a continuous model for plausible human poses based on neural distance fields (NDFs). Pose or motion priors are important for generating realistic new poses and for reconstructing accurate poses from noisy or partial observations. Pose-NDF learns a manifold of plausible poses as the zero level set of a neural implicit function, extending the idea of modeling implicit surfaces in 3D to the high-dimensional domain SO(3)^K, where a human pose is defined by a single data point, represented by K quaternions. The resulting high-dimensional implicit function can be differentiated with respect to the input poses and thus can be used to project arbitrary poses onto the manifold by using gradient descent on the set of 3-dimensional hyperspheres. In contrast to previous VAE-based human pose priors, which transform the pose space into a Gaussian distribution, we model the actual pose manifold, preserving the distances between poses. We demonstrate that PoseNDF outperforms existing state-of-the-art methods as a prior in various downstream tasks, ranging from denoising real-world human mocap data, pose recovery from occluded data to 3D pose reconstruction from images. Furthermore, we show that it can be used to generate more diverse poses by random sampling and projection than VAE-based methods.

On the Pitfalls of Heteroscedastic Uncertainty Estimation with Probabilistic Neural Networks

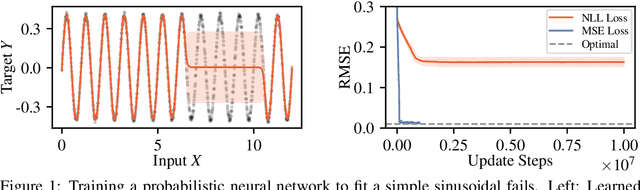
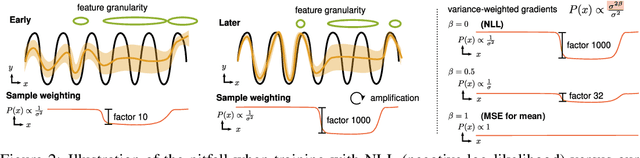
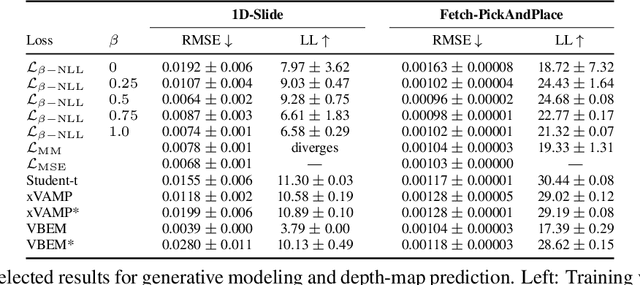
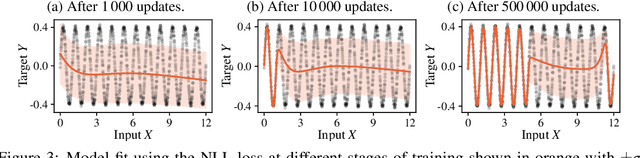
Capturing aleatoric uncertainty is a critical part of many machine learning systems. In deep learning, a common approach to this end is to train a neural network to estimate the parameters of a heteroscedastic Gaussian distribution by maximizing the logarithm of the likelihood function under the observed data. In this work, we examine this approach and identify potential hazards associated with the use of log-likelihood in conjunction with gradient-based optimizers. First, we present a synthetic example illustrating how this approach can lead to very poor but stable parameter estimates. Second, we identify the culprit to be the log-likelihood loss, along with certain conditions that exacerbate the issue. Third, we present an alternative formulation, termed $\beta$-NLL, in which each data point's contribution to the loss is weighted by the $\beta$-exponentiated variance estimate. We show that using an appropriate $\beta$ largely mitigates the issue in our illustrative example. Fourth, we evaluate this approach on a range of domains and tasks and show that it achieves considerable improvements and performs more robustly concerning hyperparameters, both in predictive RMSE and log-likelihood criteria.