Pose-NDF: Modeling Human Pose Manifolds with Neural Distance Fields
Paper and Code
Jul 27, 2022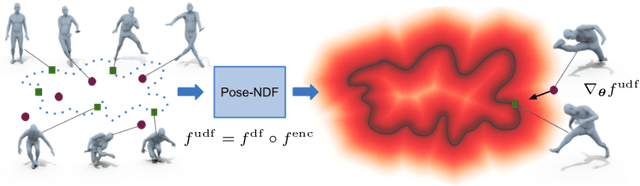
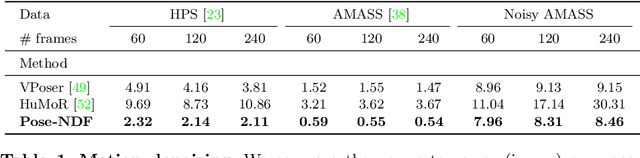
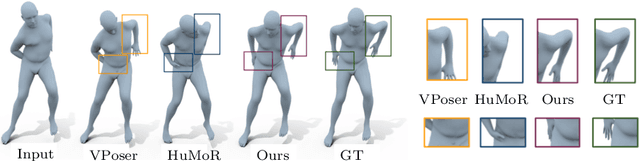
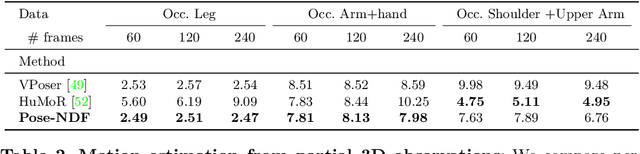
We present Pose-NDF, a continuous model for plausible human poses based on neural distance fields (NDFs). Pose or motion priors are important for generating realistic new poses and for reconstructing accurate poses from noisy or partial observations. Pose-NDF learns a manifold of plausible poses as the zero level set of a neural implicit function, extending the idea of modeling implicit surfaces in 3D to the high-dimensional domain SO(3)^K, where a human pose is defined by a single data point, represented by K quaternions. The resulting high-dimensional implicit function can be differentiated with respect to the input poses and thus can be used to project arbitrary poses onto the manifold by using gradient descent on the set of 3-dimensional hyperspheres. In contrast to previous VAE-based human pose priors, which transform the pose space into a Gaussian distribution, we model the actual pose manifold, preserving the distances between poses. We demonstrate that PoseNDF outperforms existing state-of-the-art methods as a prior in various downstream tasks, ranging from denoising real-world human mocap data, pose recovery from occluded data to 3D pose reconstruction from images. Furthermore, we show that it can be used to generate more diverse poses by random sampling and projection than VAE-based methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge