Learning in complex action spaces without policy gradients
Paper and Code
Oct 08, 2024
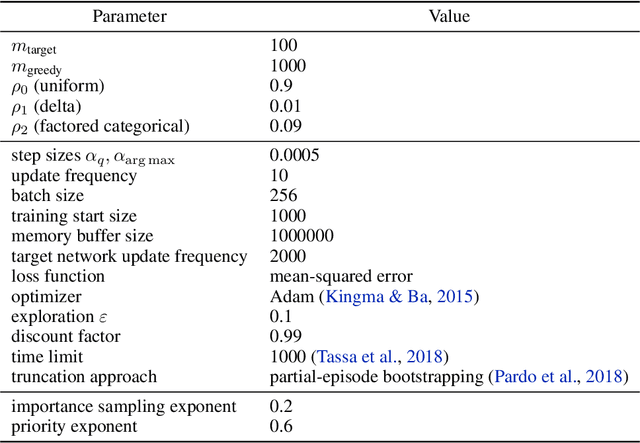
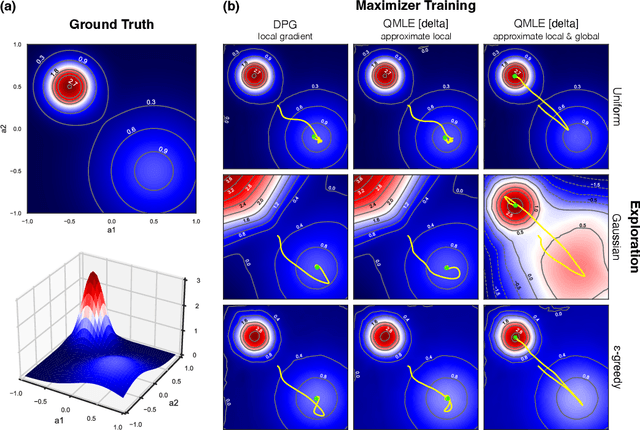
Conventional wisdom suggests that policy gradient methods are better suited to complex action spaces than action-value methods. However, foundational studies have shown equivalences between these paradigms in small and finite action spaces (O'Donoghue et al., 2017; Schulman et al., 2017a). This raises the question of why their computational applicability and performance diverge as the complexity of the action space increases. We hypothesize that the apparent superiority of policy gradients in such settings stems not from intrinsic qualities of the paradigm, but from universal principles that can also be applied to action-value methods to serve similar functionality. We identify three such principles and provide a framework for incorporating them into action-value methods. To support our hypothesis, we instantiate this framework in what we term QMLE, for Q-learning with maximum likelihood estimation. Our results show that QMLE can be applied to complex action spaces with a controllable computational cost that is comparable to that of policy gradient methods, all without using policy gradients. Furthermore, QMLE demonstrates strong performance on the DeepMind Control Suite, even when compared to the state-of-the-art methods such as DMPO and D4PG.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge