Understanding deep neural networks through the lens of their non-linearity

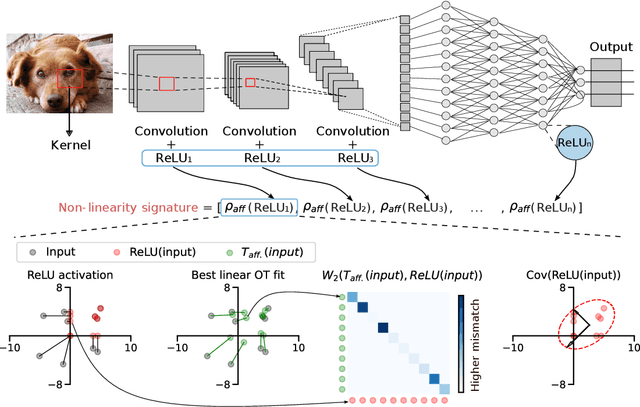
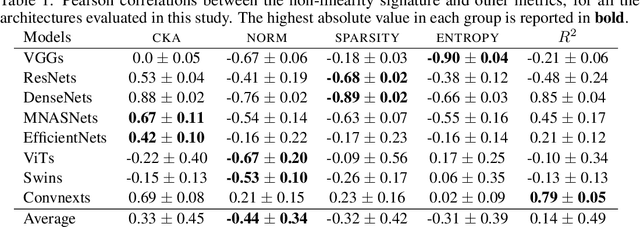
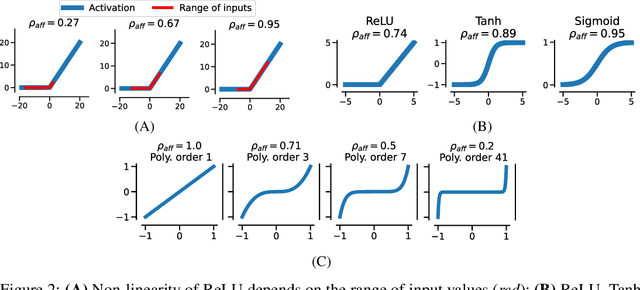
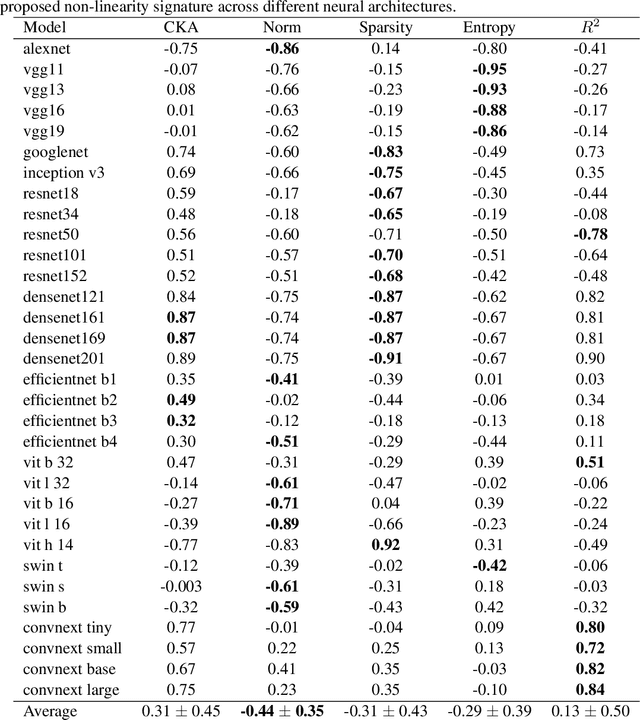
The remarkable success of deep neural networks (DNN) is often attributed to their high expressive power and their ability to approximate functions of arbitrary complexity. Indeed, DNNs are highly non-linear models, and activation functions introduced into them are largely responsible for this. While many works studied the expressive power of DNNs through the lens of their approximation capabilities, quantifying the non-linearity of DNNs or of individual activation functions remains an open problem. In this paper, we propose the first theoretically sound solution to track non-linearity propagation in deep neural networks with a specific focus on computer vision applications. Our proposed affinity score allows us to gain insights into the inner workings of a wide range of different architectures and learning paradigms. We provide extensive experimental results that highlight the practical utility of the proposed affinity score and its potential for long-reaching applications.

Beyond invariant representation learning: linearly alignable latent spaces for efficient closed-form domain adaptation

Optimal transport (OT) is a powerful geometric tool used to compare and align probability measures following the least effort principle. Among many successful applications of OT in machine learning (ML), domain adaptation (DA) -- a field of study where the goal is to transfer a classifier from one labelled domain to another similar, yet different unlabelled or scarcely labelled domain -- has been historically among the most investigated ones. This success is due to the ability of OT to provide both a meaningful discrepancy measure to assess the similarity of two domains' distributions and a mapping that can project source domain data onto the target one. In this paper, we propose a principally new OT-based approach applied to DA that uses the closed-form solution of the OT problem given by an affine mapping and learns an embedding space for which this solution is optimal and computationally less complex. We show that our approach works in both homogeneous and heterogeneous DA settings and outperforms or is on par with other famous baselines based on both traditional OT and OT in incomparable spaces. Furthermore, we show that our proposed method vastly reduces computational complexity.

Affine Transport for Sim-to-Real Domain Adaptation

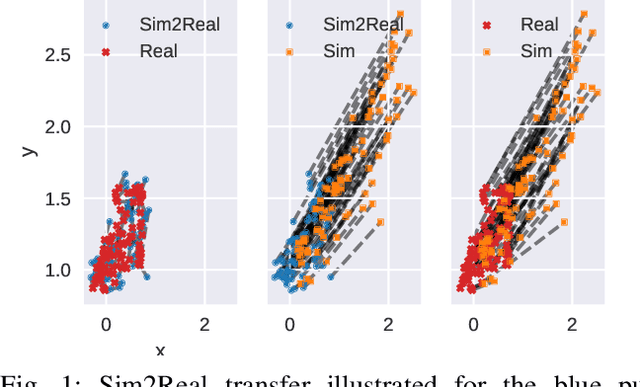
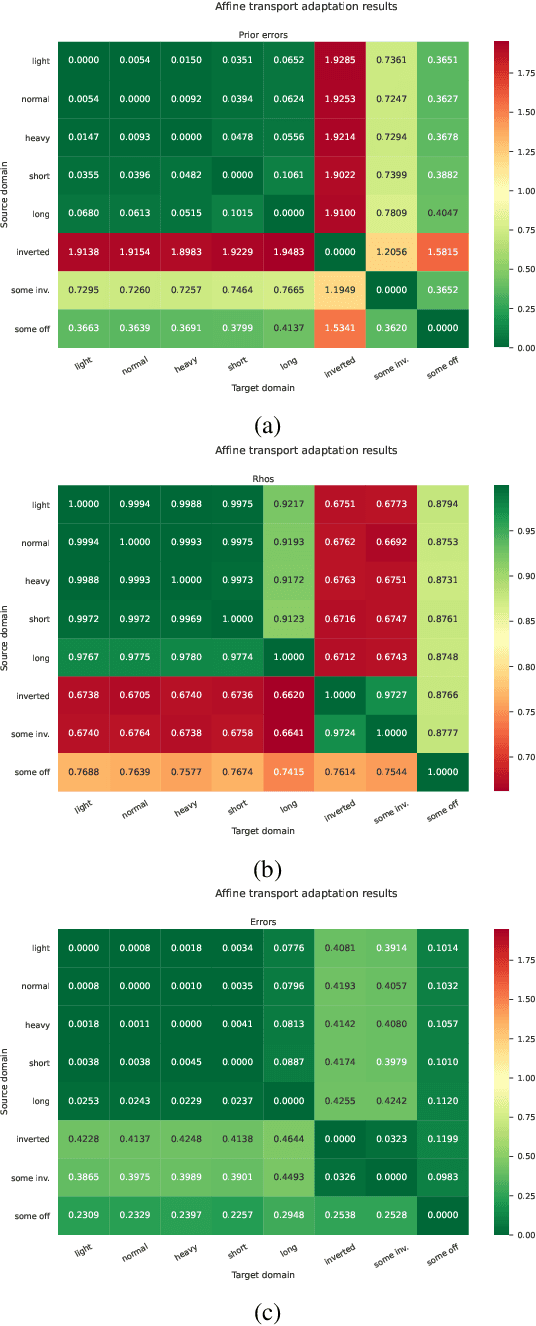
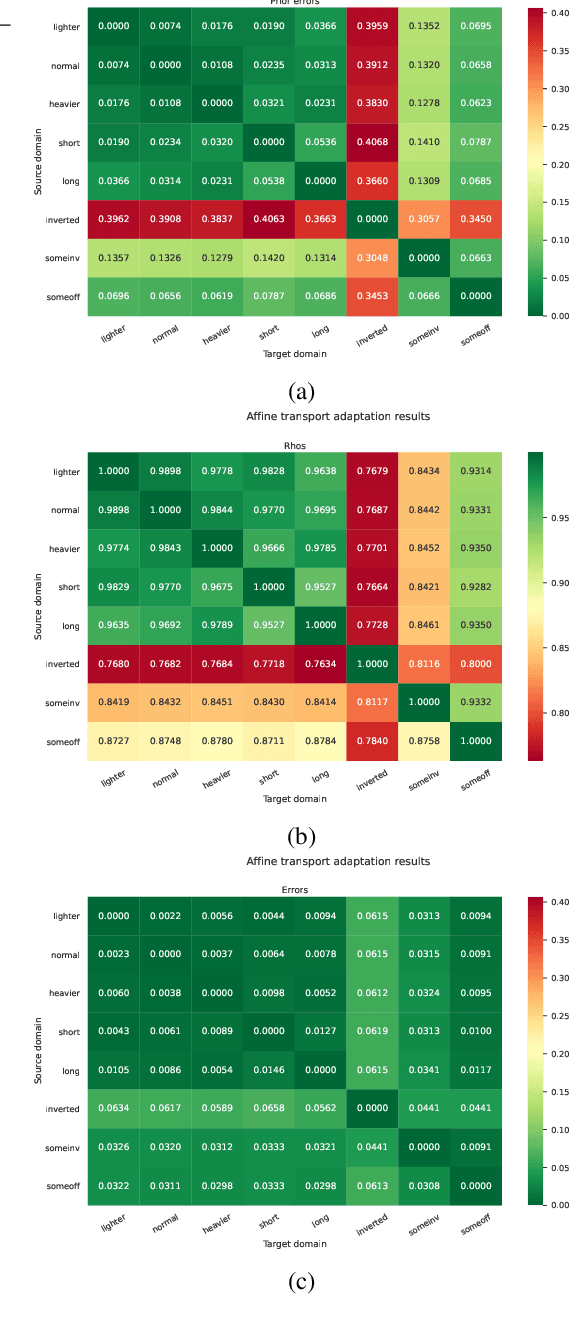
Sample-efficient domain adaptation is an open problem in robotics. In this paper, we present affine transport -- a variant of optimal transport, which models the mapping between state transition distributions between the source and target domains with an affine transformation. First, we derive the affine transport framework; then, we extend the basic framework with Procrustes alignment to model arbitrary affine transformations. We evaluate the method in a number of OpenAI Gym sim-to-sim experiments with simulation environments, as well as on a sim-to-real domain adaptation task of a robot hitting a hockeypuck such that it slides and stops at a target position. In each experiment, we evaluate the results when transferring between each pair of dynamics domains. The results show that affine transport can significantly reduce the model adaptation error in comparison to using the original, non-adapted dynamics model.

Estimating 2-Sinkhorn Divergence between Gaussian Processes from Finite-Dimensional Marginals

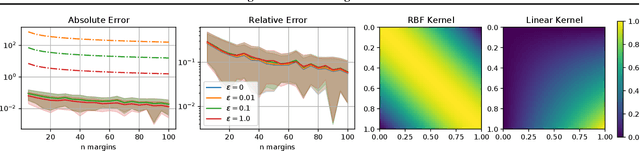
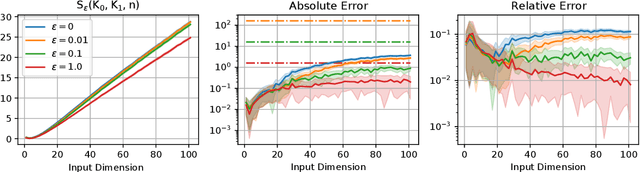
\emph{Optimal Transport} (OT) has emerged as an important computational tool in machine learning and computer vision, providing a geometrical framework for studying probability measures. OT unfortunately suffers from the curse of dimensionality and requires regularization for practical computations, of which the \emph{entropic regularization} is a popular choice, which can be 'unbiased', resulting in a \emph{Sinkhorn divergence}. In this work, we study the convergence of estimating the 2-Sinkhorn divergence between \emph{Gaussian processes} (GPs) using their finite-dimensional marginal distributions. We show almost sure convergence of the divergence when the marginals are sampled according to some base measure. Furthermore, we show that using $n$ marginals the estimation error of the divergence scales in a dimension-free way as $\mathcal{O}\left(\epsilon^ {-1}n^{-\frac{1}{2}}\right)$, where $\epsilon$ is the magnitude of entropic regularization.

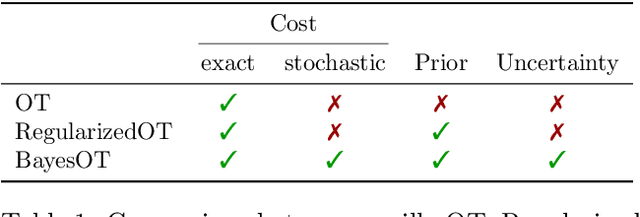
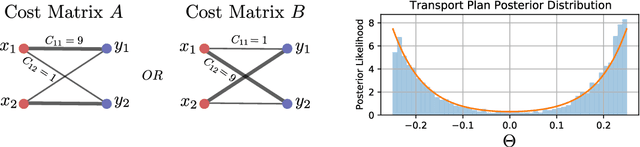
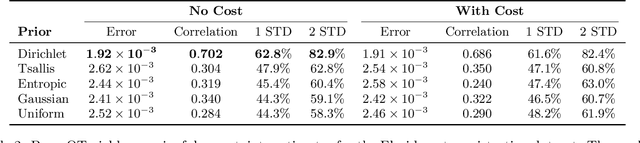
Bayesian Inference for Optimal Transport with Stochastic Cost

In machine learning and computer vision, optimal transport has had significant success in learning generative models and defining metric distances between structured and stochastic data objects, that can be cast as probability measures. The key element of optimal transport is the so called lifting of an \emph{exact} cost (distance) function, defined on the sample space, to a cost (distance) between probability measures over the sample space. However, in many real life applications the cost is \emph{stochastic}: e.g., the unpredictable traffic flow affects the cost of transportation between a factory and an outlet. To take this stochasticity into account, we introduce a Bayesian framework for inferring the optimal transport plan distribution induced by the stochastic cost, allowing for a principled way to include prior information and to model the induced stochasticity on the transport plans. Additionally, we tailor an HMC method to sample from the resulting transport plan posterior distribution.

Entropy-Regularized $2$-Wasserstein Distance between Gaussian Measures

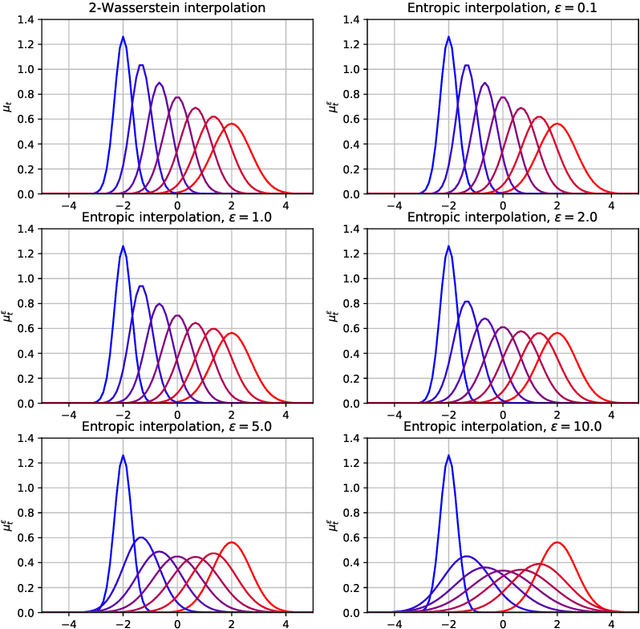
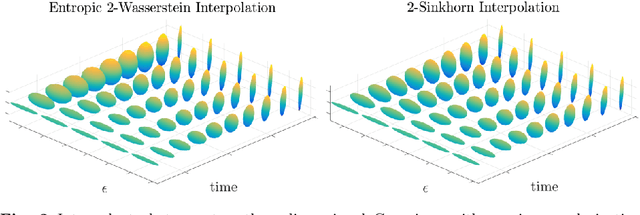
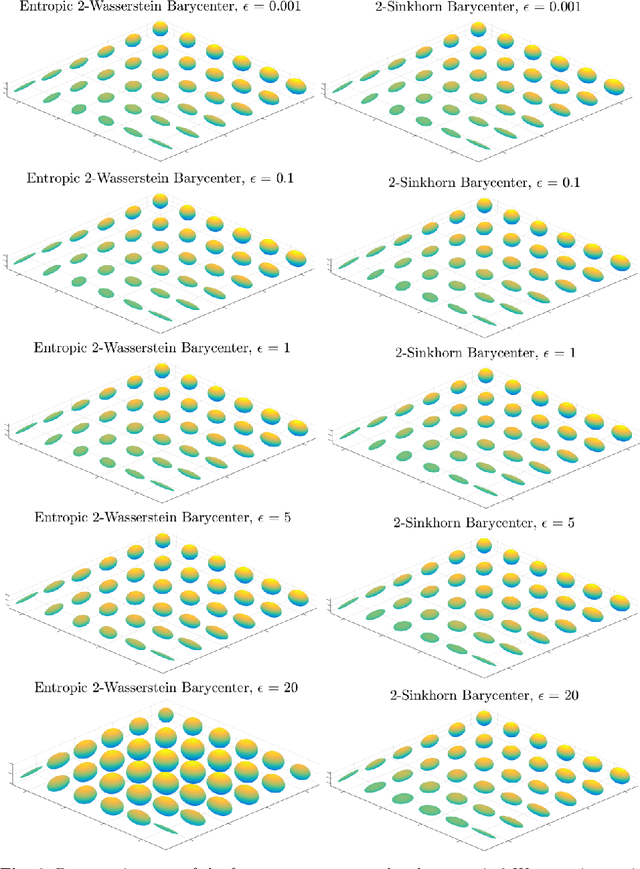
Gaussian distributions are plentiful in applications dealing in uncertainty quantification and diffusivity. They furthermore stand as important special cases for frameworks providing geometries for probability measures, as the resulting geometry on Gaussians is often expressible in closed-form under the frameworks. In this work, we study the Gaussian geometry under the entropy-regularized 2-Wasserstein distance, by providing closed-form solutions for the distance and interpolations between elements. Furthermore, we provide a fixed-point characterization of a population barycenter when restricted to the manifold of Gaussians, which allows computations through the fixed-point iteration algorithm. As a consequence, the results yield closed-form expressions for the 2-Sinkhorn divergence. As the geometries change by varying the regularization magnitude, we study the limiting cases of vanishing and infinite magnitudes, reconfirming well-known results on the limits of the Sinkhorn divergence. Finally, we illustrate the resulting geometries with a numerical study.

How Well Do WGANs Estimate the Wasserstein Metric?

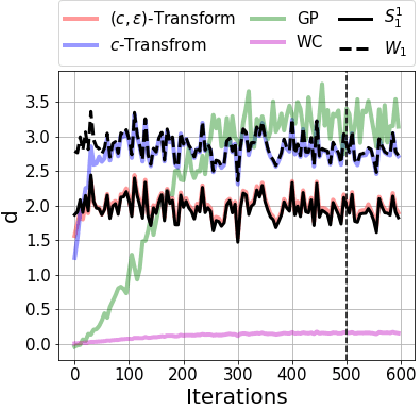
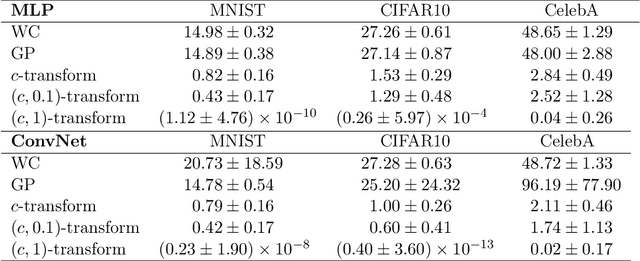
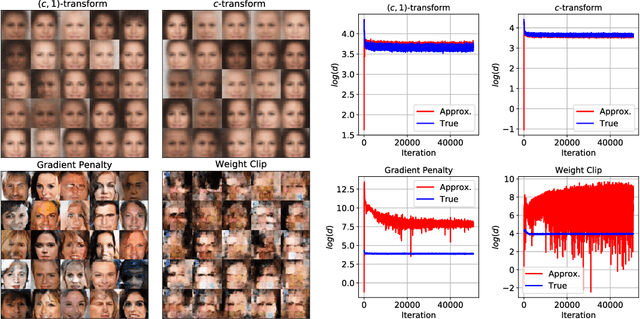
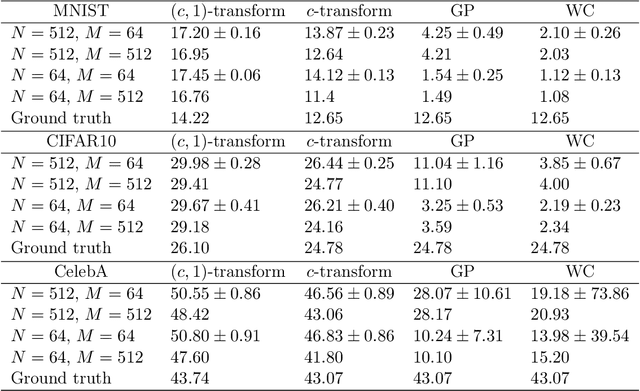
Generative modelling is often cast as minimizing a similarity measure between a data distribution and a model distribution. Recently, a popular choice for the similarity measure has been the Wasserstein metric, which can be expressed in the Kantorovich duality formulation as the optimum difference of the expected values of a potential function under the real data distribution and the model hypothesis. In practice, the potential is approximated with a neural network and is called the discriminator. Duality constraints on the function class of the discriminator are enforced approximately, and the expectations are estimated from samples. This gives at least three sources of errors: the approximated discriminator and constraints, the estimation of the expectation value, and the optimization required to find the optimal potential. In this work, we study how well the methods, that are used in generative adversarial networks to approximate the Wasserstein metric, perform. We consider, in particular, the $c$-transform formulation, which eliminates the need to enforce the constraints explicitly. We demonstrate that the $c$-transform allows for a more accurate estimation of the true Wasserstein metric from samples, but surprisingly, does not perform the best in the generative setting.

A Formalization of The Natural Gradient Method for General Similarity Measures

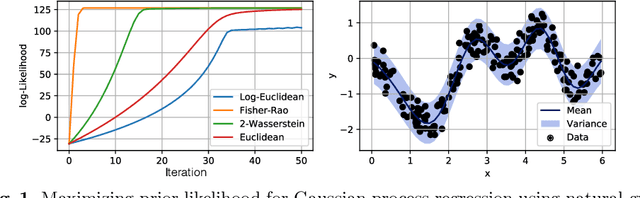
In optimization, the natural gradient method is well-known for likelihood maximization. The method uses the Kullback-Leibler divergence, corresponding infinitesimally to the Fisher-Rao metric, which is pulled back to the parameter space of a family of probability distributions. This way, gradients with respect to the parameters respect the Fisher-Rao geometry of the space of distributions, which might differ vastly from the standard Euclidean geometry of the parameter space, often leading to faster convergence. However, when minimizing an arbitrary similarity measure between distributions, it is generally unclear which metric to use. We provide a general framework that, given a similarity measure, derives a metric for the natural gradient. We then discuss connections between the natural gradient method and multiple other optimization techniques in the literature. Finally, we provide computations of the formal natural gradient to show overlap with well-known cases and to compute natural gradients in novel frameworks.

(q,p)-Wasserstein GANs: Comparing Ground Metrics for Wasserstein GANs

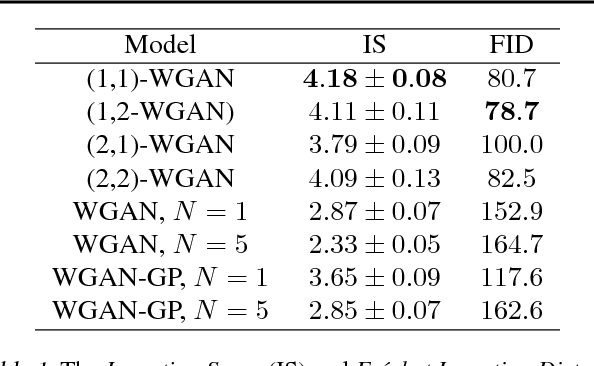
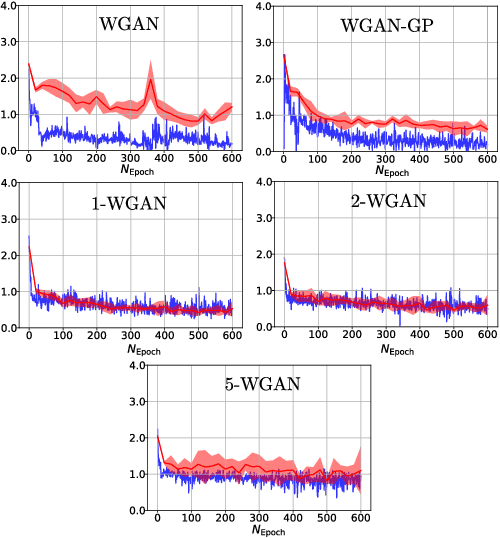
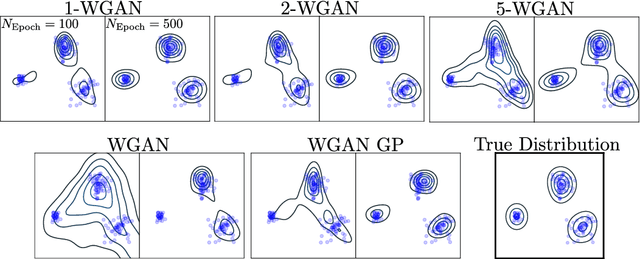
Generative Adversial Networks (GANs) have made a major impact in computer vision and machine learning as generative models. Wasserstein GANs (WGANs) brought Optimal Transport (OT) theory into GANs, by minimizing the $1$-Wasserstein distance between model and data distributions as their objective function. Since then, WGANs have gained considerable interest due to their stability and theoretical framework. We contribute to the WGAN literature by introducing the family of $(q,p)$-Wasserstein GANs, which allow the use of more general $p$-Wasserstein metrics for $p\geq 1$ in the GAN learning procedure. While the method is able to incorporate any cost function as the ground metric, we focus on studying the $l^q$ metrics for $q\geq 1$. This is a notable generalization as in the WGAN literature the OT distances are commonly based on the $l^2$ ground metric. We demonstrate the effect of different $p$-Wasserstein distances in two toy examples. Furthermore, we show that the ground metric does make a difference, by comparing different $(q,p)$ pairs on the MNIST and CIFAR-10 datasets. Our experiments demonstrate that changing the ground metric and $p$ can notably improve on the common $(q,p) = (2,1)$ case.

Probabilistic Riemannian submanifold learning with wrapped Gaussian process latent variable models

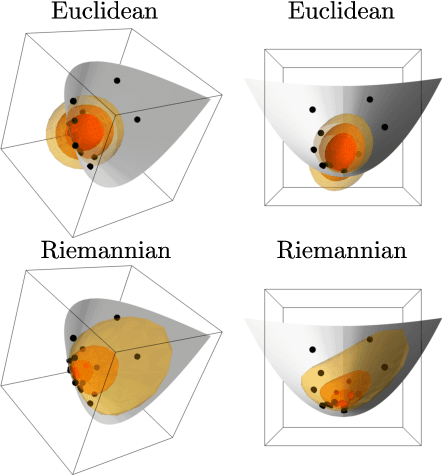
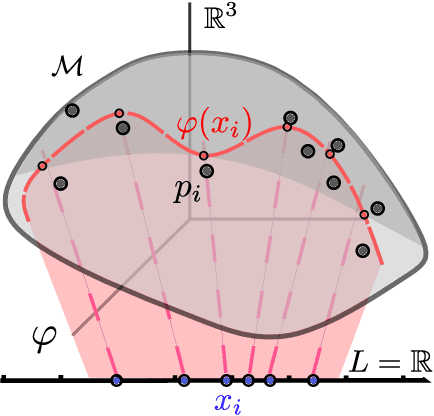
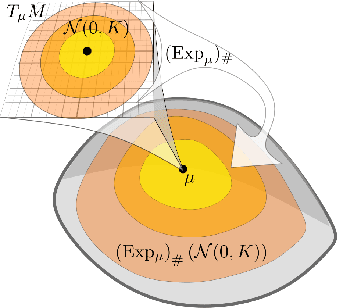
Latent variable models learn a stochastic embedding from a low-dimensional latent space onto a submanifold of the Euclidean input space, on which the data is assumed to lie. Frequently, however, the data objects are known to satisfy constraints or invariances, which are not enforced by traditional latent variable models. As a result, significant probability mass is assigned to points that violate the known constraints. To remedy this, we propose the wrapped Gaussian process latent variable model (WGPLVM). The model allows non-linear, probabilistic inference of a lower-dimensional submanifold where data is assumed to reside, while respecting known constraints or invariances encoded in a Riemannian manifold. We evaluate our model against the Euclidean GPLVM on several datasets and tasks, including encoding, visualization and uncertainty quantification.