Entropy-Regularized $2$-Wasserstein Distance between Gaussian Measures

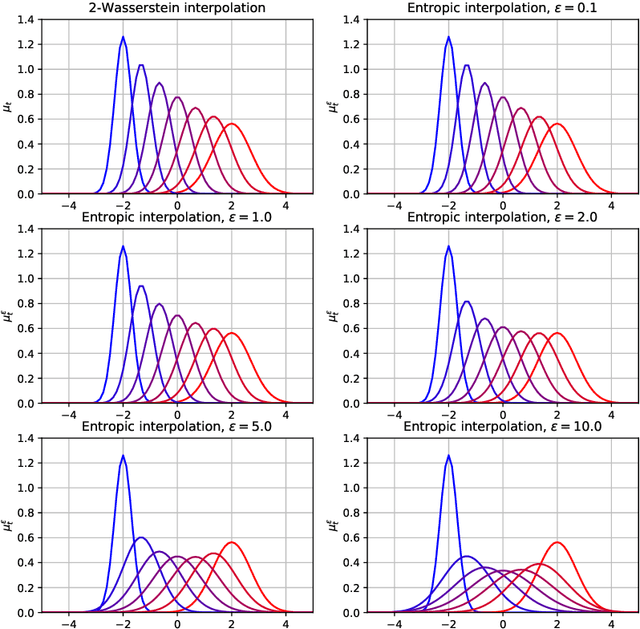
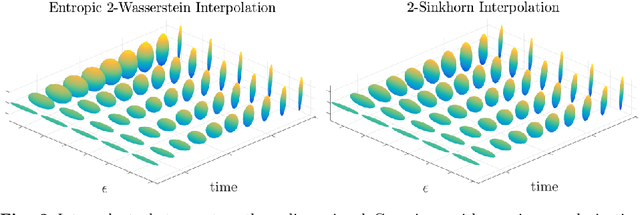
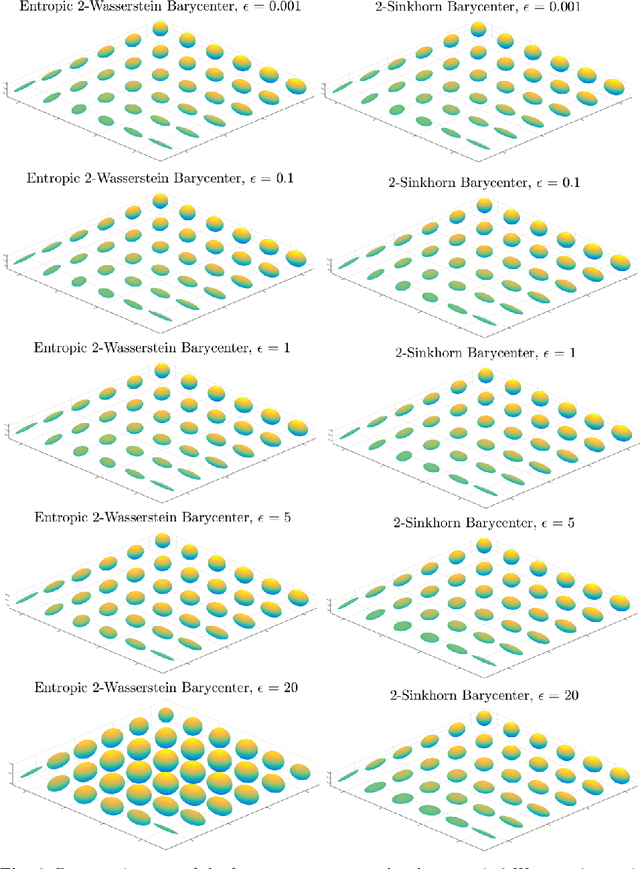
Gaussian distributions are plentiful in applications dealing in uncertainty quantification and diffusivity. They furthermore stand as important special cases for frameworks providing geometries for probability measures, as the resulting geometry on Gaussians is often expressible in closed-form under the frameworks. In this work, we study the Gaussian geometry under the entropy-regularized 2-Wasserstein distance, by providing closed-form solutions for the distance and interpolations between elements. Furthermore, we provide a fixed-point characterization of a population barycenter when restricted to the manifold of Gaussians, which allows computations through the fixed-point iteration algorithm. As a consequence, the results yield closed-form expressions for the 2-Sinkhorn divergence. As the geometries change by varying the regularization magnitude, we study the limiting cases of vanishing and infinite magnitudes, reconfirming well-known results on the limits of the Sinkhorn divergence. Finally, we illustrate the resulting geometries with a numerical study.

Kernel Methods on Approximate Infinite-Dimensional Covariance Operators for Image Classification

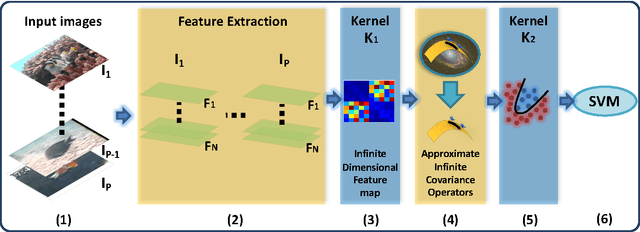
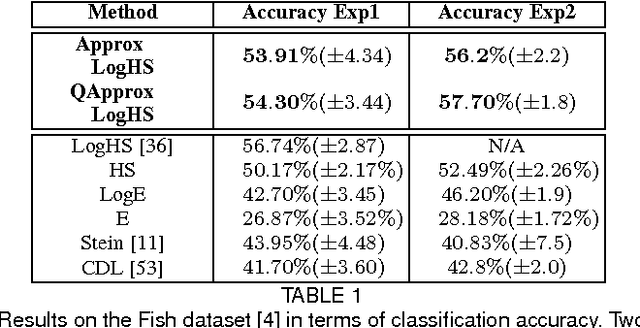
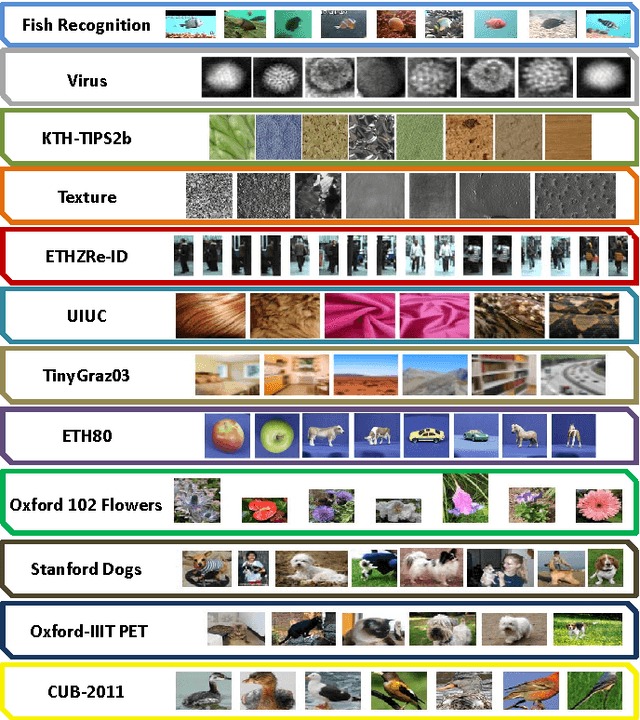
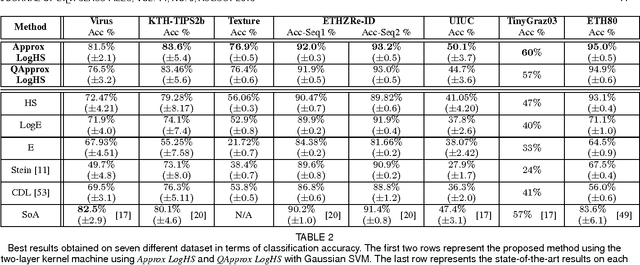
This paper presents a novel framework for visual object recognition using infinite-dimensional covariance operators of input features in the paradigm of kernel methods on infinite-dimensional Riemannian manifolds. Our formulation provides in particular a rich representation of image features by exploiting their non-linear correlations. Theoretically, we provide a finite-dimensional approximation of the Log-Hilbert-Schmidt (Log-HS) distance between covariance operators that is scalable to large datasets, while maintaining an effective discriminating capability. This allows us to efficiently approximate any continuous shift-invariant kernel defined using the Log-HS distance. At the same time, we prove that the Log-HS inner product between covariance operators is only approximable by its finite-dimensional counterpart in a very limited scenario. Consequently, kernels defined using the Log-HS inner product, such as polynomial kernels, are not scalable in the same way as shift-invariant kernels. Computationally, we apply the approximate Log-HS distance formulation to covariance operators of both handcrafted and convolutional features, exploiting both the expressiveness of these features and the power of the covariance representation. Empirically, we tested our framework on the task of image classification on twelve challenging datasets. In almost all cases, the results obtained outperform other state of the art methods, demonstrating the competitiveness and potential of our framework.