Categorical and geometric methods in statistical, manifold, and machine learning

We present and discuss applications of the category of probabilistic morphisms, initially developed in \cite{Le2023}, as well as some geometric methods to several classes of problems in statistical, machine and manifold learning which shall be, along with many other topics, considered in depth in the forthcoming book \cite{LMPT2024}.

Supervised learning with probabilistic morphisms and kernel mean embeddings

In this paper I propose a concept of a correct loss function in a generative model of supervised learning for an input space $\mathcal{X}$ and a label space $\mathcal{Y}$, which are measurable spaces. A correct loss function in a generative model of supervised learning must correctly measure the discrepancy between elements of a hypothesis space $\mathcal{H}$ of possible predictors and the supervisor operator, which may not belong to $\mathcal{H}$. To define correct loss functions, I propose a characterization of a regular conditional probability measure $\mu_{\mathcal{Y}|\mathcal{X}}$ for a probability measure $\mu$ on $\mathcal{X} \times \mathcal{Y}$ relative to the projection $\Pi_{\mathcal{X}}: \mathcal{X}\times\mathcal{Y}\to \mathcal{X}$ as a solution of a linear operator equation. If $\mathcal{Y}$ is a separable metrizable topological space with the Borel $\sigma$-algebra $ \mathcal{B} (\mathcal{Y})$, I propose another characterization of a regular conditional probability measure $\mu_{\mathcal{Y}|\mathcal{X}}$ as a minimizer of a mean square error on the space of Markov kernels, called probabilistic morphisms, from $\mathcal{X}$ to $\mathcal{Y}$, using kernel mean embeddings. Using these results and using inner measure to quantify generalizability of a learning algorithm, I give a generalization of a result due to Cucker-Smale, which concerns the learnability of a regression model, to a setting of a conditional probability estimation problem. I also give a variant of Vapnik's regularization method for solving stochastic ill-posed problems, using inner measure, and present its applications.

Epidemic Dynamics via Wavelet Theory and Machine Learning, with Applications to Covid-19

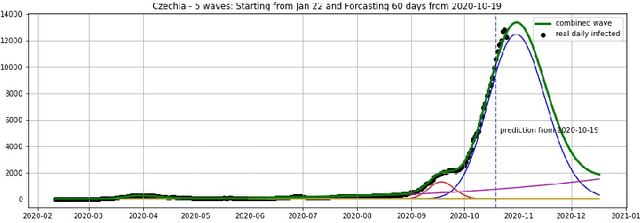
We introduce the concept of epidemic-fitted wavelets which comprise, in particular, as special cases the number $I(t)$ of infectious individuals at time $t$ in classical SIR models and their derivatives. We present a novel method for modelling epidemic dynamics by a model selection method using wavelet theory and, for its applications, machine learning based curve fitting techniques. Our universal models are functions that are finite linear combinations of epidemic-fitted wavelets. We apply our method by modelling and forecasting, based on the John Hopkins University dataset, the spread of the current Covid-19 (SARS-CoV-2) epidemic in France, Germany, Italy and the Czech Republic, as well as in the US federal states New York and Florida.