Categorical and geometric methods in statistical, manifold, and machine learning

We present and discuss applications of the category of probabilistic morphisms, initially developed in \cite{Le2023}, as well as some geometric methods to several classes of problems in statistical, machine and manifold learning which shall be, along with many other topics, considered in depth in the forthcoming book \cite{LMPT2024}.

A cohomology-based Gromov-Hausdorff metric approach for quantifying molecular similarity

We introduce, for the first time, a cohomology-based Gromov-Hausdorff ultrametric method to analyze 1-dimensional and higher-dimensional (co)homology groups, focusing on loops, voids, and higher-dimensional cavity structures in simplicial complexes, to address typical clustering questions arising in molecular data analysis. The Gromov-Hausdorff distance quantifies the dissimilarity between two metric spaces. In this framework, molecules are represented as simplicial complexes, and their cohomology vector spaces are computed to capture intrinsic topological invariants encoding loop and cavity structures. These vector spaces are equipped with a suitable distance measure, enabling the computation of the Gromov-Hausdorff ultrametric to evaluate structural dissimilarities. We demonstrate the methodology using organic-inorganic halide perovskite (OIHP) structures. The results highlight the effectiveness of this approach in clustering various molecular structures. By incorporating geometric information, our method provides deeper insights compared to traditional persistent homology techniques.

Epidemic Dynamics via Wavelet Theory and Machine Learning, with Applications to Covid-19

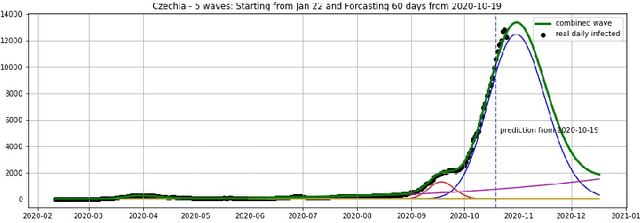
We introduce the concept of epidemic-fitted wavelets which comprise, in particular, as special cases the number $I(t)$ of infectious individuals at time $t$ in classical SIR models and their derivatives. We present a novel method for modelling epidemic dynamics by a model selection method using wavelet theory and, for its applications, machine learning based curve fitting techniques. Our universal models are functions that are finite linear combinations of epidemic-fitted wavelets. We apply our method by modelling and forecasting, based on the John Hopkins University dataset, the spread of the current Covid-19 (SARS-CoV-2) epidemic in France, Germany, Italy and the Czech Republic, as well as in the US federal states New York and Florida.