Kelin Xia
Rhomboid Tiling for Geometric Graph Deep Learning
May 14, 2025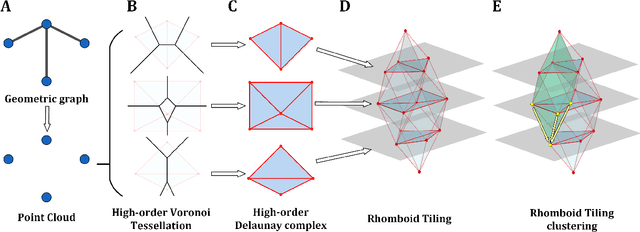
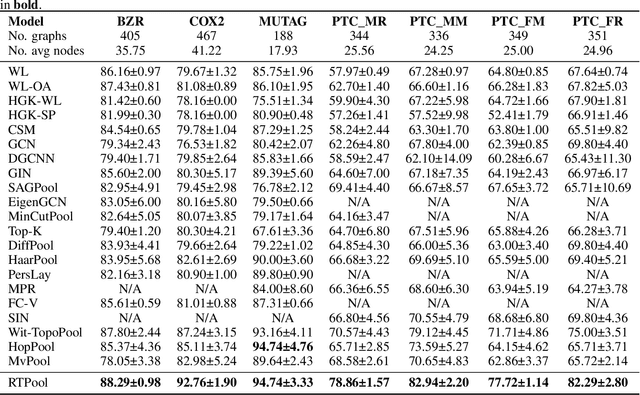
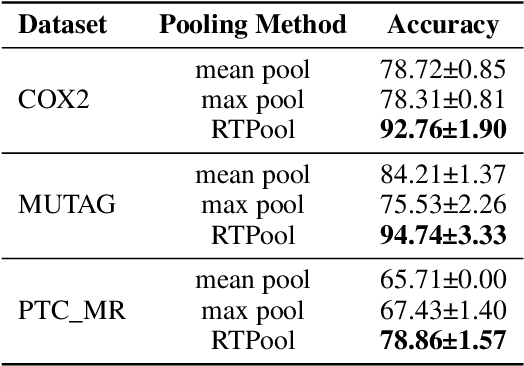
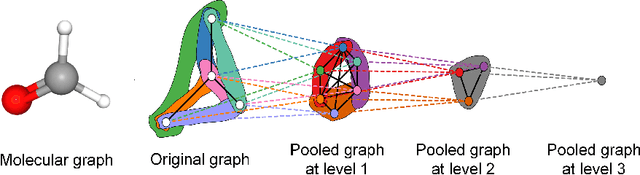
Abstract:Graph Neural Networks (GNNs) have proven effective for learning from graph-structured data through their neighborhood-based message passing framework. Many hierarchical graph clustering pooling methods modify this framework by introducing clustering-based strategies, enabling the construction of more expressive and powerful models. However, all of these message passing framework heavily rely on the connectivity structure of graphs, limiting their ability to capture the rich geometric features inherent in geometric graphs. To address this, we propose Rhomboid Tiling (RT) clustering, a novel clustering method based on the rhomboid tiling structure, which performs clustering by leveraging the complex geometric information of the data and effectively extracts its higher-order geometric structures. Moreover, we design RTPool, a hierarchical graph clustering pooling model based on RT clustering for graph classification tasks. The proposed model demonstrates superior performance, outperforming 21 state-of-the-art competitors on all the 7 benchmark datasets.
Quotient Complex Transformer (QCformer) for Perovskite Data Analysis
May 14, 2025Abstract:The discovery of novel functional materials is crucial in addressing the challenges of sustainable energy generation and climate change. Hybrid organic-inorganic perovskites (HOIPs) have gained attention for their exceptional optoelectronic properties in photovoltaics. Recently, geometric deep learning, particularly graph neural networks (GNNs), has shown strong potential in predicting material properties and guiding material design. However, traditional GNNs often struggle to capture the periodic structures and higher-order interactions prevalent in such systems. To address these limitations, we propose a novel representation based on quotient complexes (QCs) and introduce the Quotient Complex Transformer (QCformer) for material property prediction. A material structure is modeled as a quotient complex, which encodes both pairwise and many-body interactions via simplices of varying dimensions and captures material periodicity through a quotient operation. Our model leverages higher-order features defined on simplices and processes them using a simplex-based Transformer module. We pretrain QCformer on benchmark datasets such as the Materials Project and JARVIS, and fine-tune it on HOIP datasets. The results show that QCformer outperforms state-of-the-art models in HOIP property prediction, demonstrating its effectiveness. The quotient complex representation and QCformer model together contribute a powerful new tool for predictive modeling of perovskite materials.
A cohomology-based Gromov-Hausdorff metric approach for quantifying molecular similarity
Nov 21, 2024Abstract:We introduce, for the first time, a cohomology-based Gromov-Hausdorff ultrametric method to analyze 1-dimensional and higher-dimensional (co)homology groups, focusing on loops, voids, and higher-dimensional cavity structures in simplicial complexes, to address typical clustering questions arising in molecular data analysis. The Gromov-Hausdorff distance quantifies the dissimilarity between two metric spaces. In this framework, molecules are represented as simplicial complexes, and their cohomology vector spaces are computed to capture intrinsic topological invariants encoding loop and cavity structures. These vector spaces are equipped with a suitable distance measure, enabling the computation of the Gromov-Hausdorff ultrametric to evaluate structural dissimilarities. We demonstrate the methodology using organic-inorganic halide perovskite (OIHP) structures. The results highlight the effectiveness of this approach in clustering various molecular structures. By incorporating geometric information, our method provides deeper insights compared to traditional persistent homology techniques.
KA-GNN: Kolmogorov-Arnold Graph Neural Networks for Molecular Property Prediction
Oct 15, 2024Abstract:Molecular property prediction is a crucial task in the process of Artificial Intelligence-Driven Drug Discovery (AIDD). The challenge of developing models that surpass traditional non-neural network methods continues to be a vibrant area of research. This paper presents a novel graph neural network model-the Kolmogorov-Arnold Network (KAN)-based Graph Neural Network (KA-GNN), which incorporates Fourier series, specifically designed for molecular property prediction. This model maintains the high interpretability characteristic of KAN methods while being extremely efficient in computational resource usage, making it an ideal choice for deployment in resource-constrained environments. Tested and validated on seven public datasets, KA-GNN has shown significant improvements in property predictions over the existing state-of-the-art (SOTA) benchmarks.
Molecular topological deep learning for polymer property prediction
Oct 07, 2024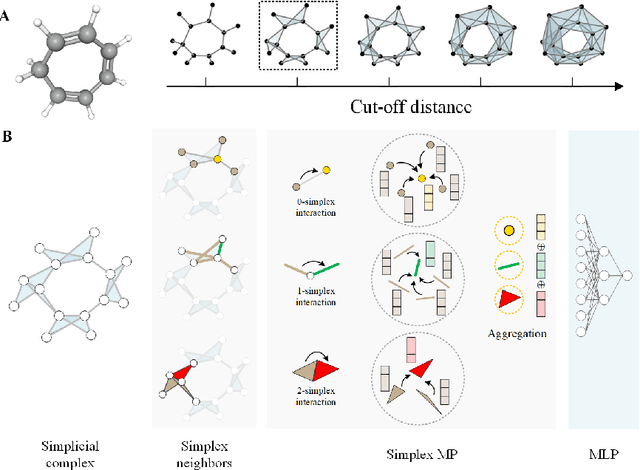
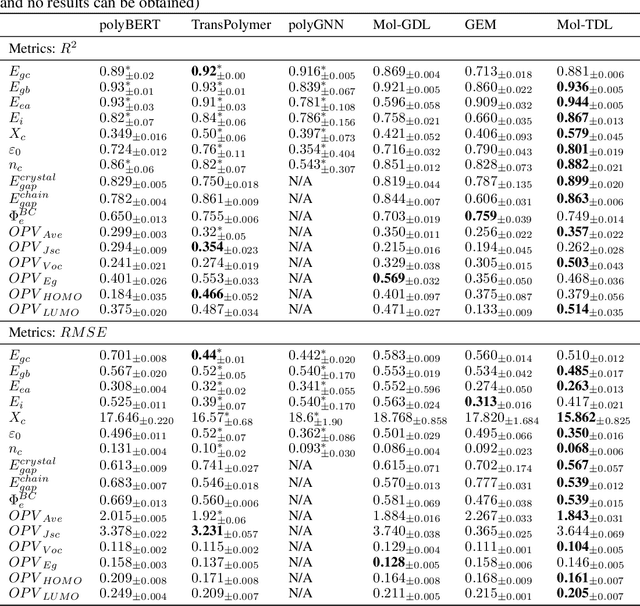
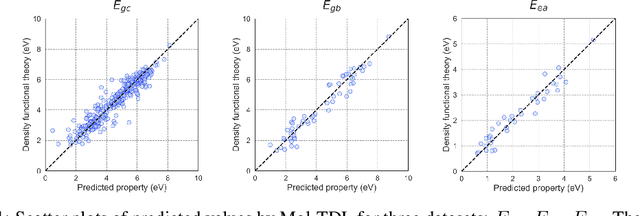
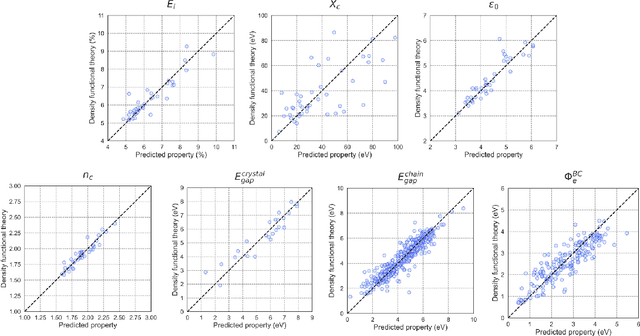
Abstract:Accurate and efficient prediction of polymer properties is of key importance for polymer design. Traditional experimental tools and density function theory (DFT)-based simulations for polymer property evaluation, are both expensive and time-consuming. Recently, a gigantic amount of graph-based molecular models have emerged and demonstrated huge potential in molecular data analysis. Even with the great progresses, these models tend to ignore the high-order and mutliscale information within the data. In this paper, we develop molecular topological deep learning (Mol-TDL) for polymer property analysis. Our Mol-TDL incorporates both high-order interactions and multiscale properties into topological deep learning architecture. The key idea is to represent polymer molecules as a series of simplicial complices at different scales and build up simplical neural networks accordingly. The aggregated information from different scales provides a more accurate prediction of polymer molecular properties.
Topology-enhanced machine learning model (Top-ML) for anticancer peptide prediction
Jul 12, 2024Abstract:Recently, therapeutic peptides have demonstrated great promise for cancer treatment. To explore powerful anticancer peptides, artificial intelligence (AI)-based approaches have been developed to systematically screen potential candidates. However, the lack of efficient featurization of peptides has become a bottleneck for these machine-learning models. In this paper, we propose a topology-enhanced machine learning model (Top-ML) for anticancer peptide prediction. Our Top-ML employs peptide topological features derived from its sequence "connection" information characterized by vector and spectral descriptors. Our Top-ML model has been validated on two widely used AntiCP 2.0 benchmark datasets and has achieved state-of-the-art performance. Our results highlight the potential of leveraging novel topology-based featurization to accelerate the identification of anticancer peptides.
Graph Neural Networks with a Distribution of Parametrized Graphs
Oct 28, 2023Abstract:Traditionally, graph neural networks have been trained using a single observed graph. However, the observed graph represents only one possible realization. In many applications, the graph may encounter uncertainties, such as having erroneous or missing edges, as well as edge weights that provide little informative value. To address these challenges and capture additional information previously absent in the observed graph, we introduce latent variables to parameterize and generate multiple graphs. We obtain the maximum likelihood estimate of the network parameters in an Expectation-Maximization (EM) framework based on the multiple graphs. Specifically, we iteratively determine the distribution of the graphs using a Markov Chain Monte Carlo (MCMC) method, incorporating the principles of PAC-Bayesian theory. Numerical experiments demonstrate improvements in performance against baseline models on node classification for heterogeneous graphs and graph regression on chemistry datasets.
Torsion Graph Neural Networks
Jun 23, 2023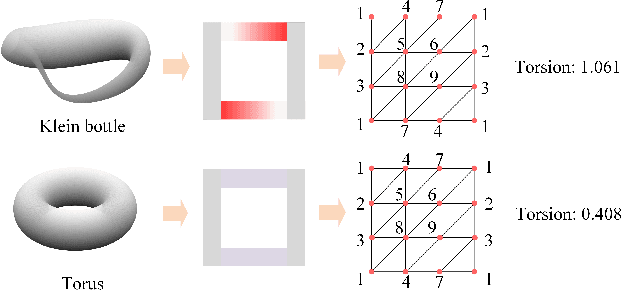
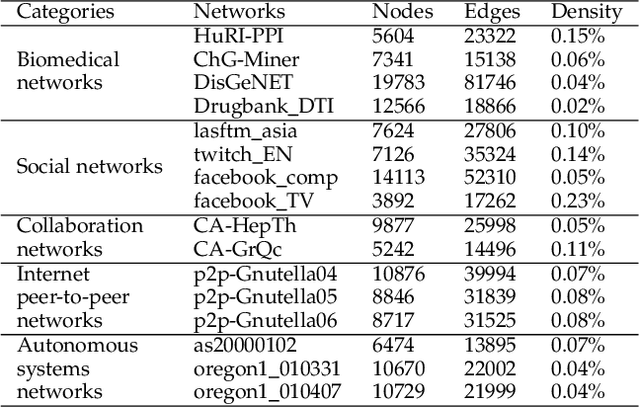


Abstract:Geometric deep learning (GDL) models have demonstrated a great potential for the analysis of non-Euclidian data. They are developed to incorporate the geometric and topological information of non-Euclidian data into the end-to-end deep learning architectures. Motivated by the recent success of discrete Ricci curvature in graph neural network (GNNs), we propose TorGNN, an analytic Torsion enhanced Graph Neural Network model. The essential idea is to characterize graph local structures with an analytic torsion based weight formula. Mathematically, analytic torsion is a topological invariant that can distinguish spaces which are homotopy equivalent but not homeomorphic. In our TorGNN, for each edge, a corresponding local simplicial complex is identified, then the analytic torsion (for this local simplicial complex) is calculated, and further used as a weight (for this edge) in message-passing process. Our TorGNN model is validated on link prediction tasks from sixteen different types of networks and node classification tasks from three types of networks. It has been found that our TorGNN can achieve superior performance on both tasks, and outperform various state-of-the-art models. This demonstrates that analytic torsion is a highly efficient topological invariant in the characterization of graph structures and can significantly boost the performance of GNNs.
Curvature-enhanced Graph Convolutional Network for Biomolecular Interaction Prediction
Jun 23, 2023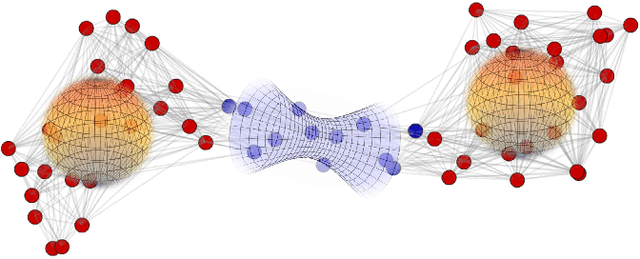
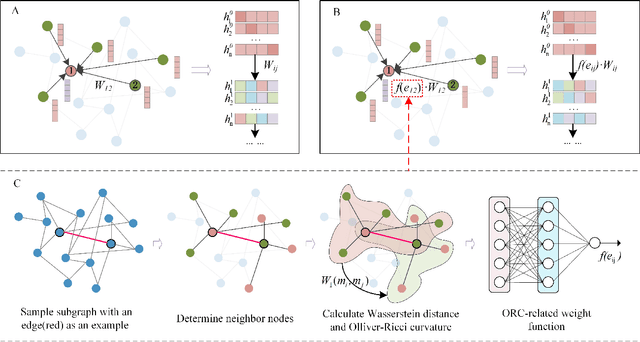
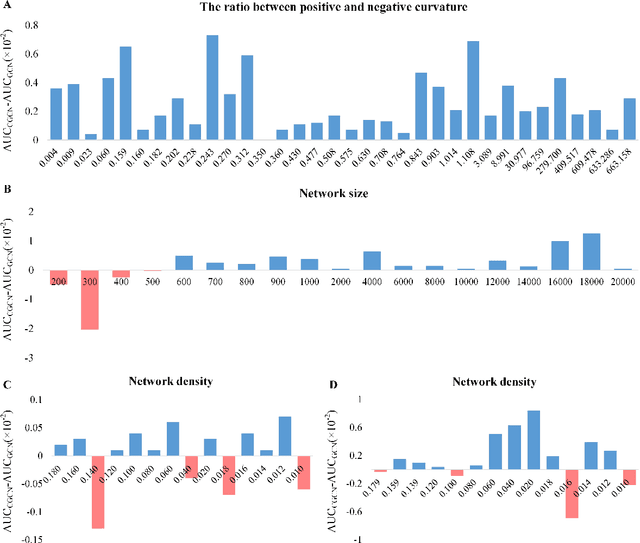
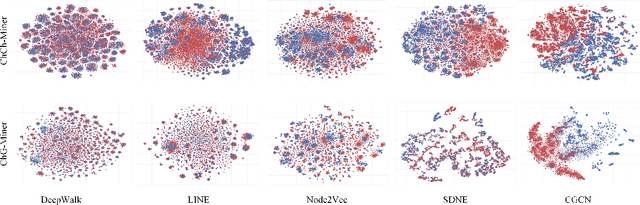
Abstract:Geometric deep learning has demonstrated a great potential in non-Euclidean data analysis. The incorporation of geometric insights into learning architecture is vital to its success. Here we propose a curvature-enhanced graph convolutional network (CGCN) for biomolecular interaction prediction, for the first time. Our CGCN employs Ollivier-Ricci curvature (ORC) to characterize network local structures and to enhance the learning capability of GCNs. More specifically, ORCs are evaluated based on the local topology from node neighborhoods, and further used as weights for the feature aggregation in message-passing procedure. Our CGCN model is extensively validated on fourteen real-world bimolecular interaction networks and a series of simulated data. It has been found that our CGCN can achieve the state-of-the-art results. It outperforms all existing models, as far as we know, in thirteen out of the fourteen real-world datasets and ranks as the second in the rest one. The results from the simulated data show that our CGCN model is superior to the traditional GCN models regardless of the positive-to-negativecurvature ratios, network densities, and network sizes (when larger than 500).
Molecular geometric deep learning
Jun 22, 2023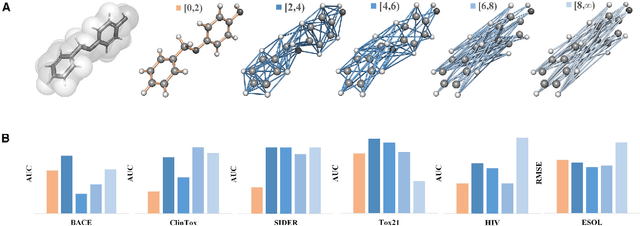
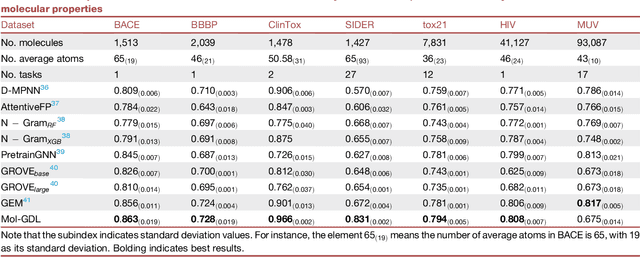
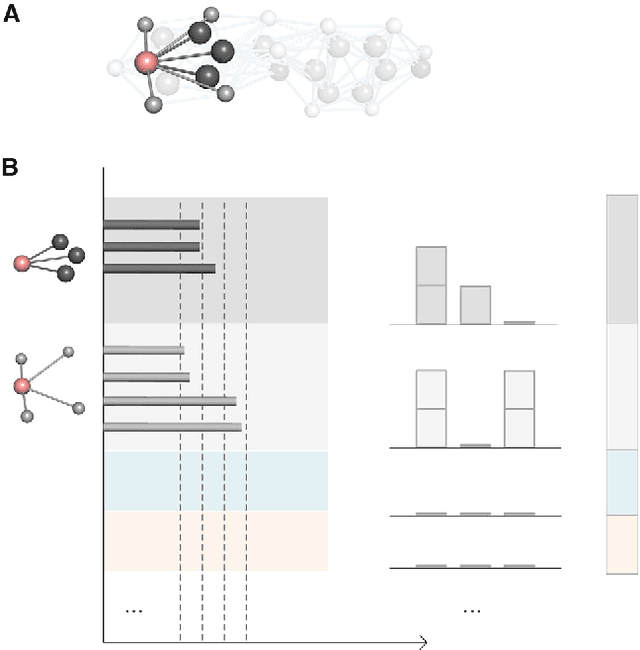
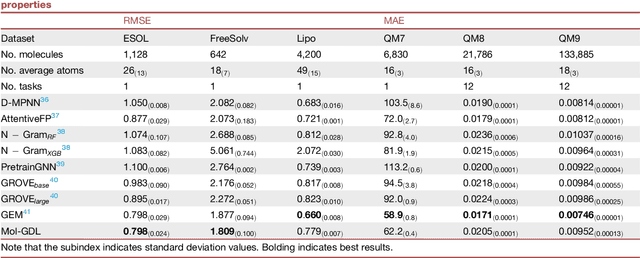
Abstract:Geometric deep learning (GDL) has demonstrated huge power and enormous potential in molecular data analysis. However, a great challenge still remains for highly efficient molecular representations. Currently, covalent-bond-based molecular graphs are the de facto standard for representing molecular topology at the atomic level. Here we demonstrate, for the first time, that molecular graphs constructed only from non-covalent bonds can achieve similar or even better results than covalent-bond-based models in molecular property prediction. This demonstrates the great potential of novel molecular representations beyond the de facto standard of covalent-bond-based molecular graphs. Based on the finding, we propose molecular geometric deep learning (Mol-GDL). The essential idea is to incorporate a more general molecular representation into GDL models. In our Mol-GDL, molecular topology is modeled as a series of molecular graphs, each focusing on a different scale of atomic interactions. In this way, both covalent interactions and non-covalent interactions are incorporated into the molecular representation on an equal footing. We systematically test Mol-GDL on fourteen commonly-used benchmark datasets. The results show that our Mol-GDL can achieve a better performance than state-of-the-art (SOTA) methods. Source code and data are available at https://github.com/CS-BIO/Mol-GDL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge