Graph Neural Networks with a Distribution of Parametrized Graphs

Traditionally, graph neural networks have been trained using a single observed graph. However, the observed graph represents only one possible realization. In many applications, the graph may encounter uncertainties, such as having erroneous or missing edges, as well as edge weights that provide little informative value. To address these challenges and capture additional information previously absent in the observed graph, we introduce latent variables to parameterize and generate multiple graphs. We obtain the maximum likelihood estimate of the network parameters in an Expectation-Maximization (EM) framework based on the multiple graphs. Specifically, we iteratively determine the distribution of the graphs using a Markov Chain Monte Carlo (MCMC) method, incorporating the principles of PAC-Bayesian theory. Numerical experiments demonstrate improvements in performance against baseline models on node classification for heterogeneous graphs and graph regression on chemistry datasets.

Leveraging Label Non-Uniformity for Node Classification in Graph Neural Networks

In node classification using graph neural networks (GNNs), a typical model generates logits for different class labels at each node. A softmax layer often outputs a label prediction based on the largest logit. We demonstrate that it is possible to infer hidden graph structural information from the dataset using these logits. We introduce the key notion of label non-uniformity, which is derived from the Wasserstein distance between the softmax distribution of the logits and the uniform distribution. We demonstrate that nodes with small label non-uniformity are harder to classify correctly. We theoretically analyze how the label non-uniformity varies across the graph, which provides insights into boosting the model performance: increasing training samples with high non-uniformity or dropping edges to reduce the maximal cut size of the node set of small non-uniformity. These mechanisms can be easily added to a base GNN model. Experimental results demonstrate that our approach improves the performance of many benchmark base models.

Distributional Signals for Node Classification in Graph Neural Networks

In graph neural networks (GNNs), both node features and labels are examples of graph signals, a key notion in graph signal processing (GSP). While it is common in GSP to impose signal smoothness constraints in learning and estimation tasks, it is unclear how this can be done for discrete node labels. We bridge this gap by introducing the concept of distributional graph signals. In our framework, we work with the distributions of node labels instead of their values and propose notions of smoothness and non-uniformity of such distributional graph signals. We then propose a general regularization method for GNNs that allows us to encode distributional smoothness and non-uniformity of the model output in semi-supervised node classification tasks. Numerical experiments demonstrate that our method can significantly improve the performance of most base GNN models in different problem settings.

Node-Specific Space Selection via Localized Geometric Hyperbolicity in Graph Neural Networks

Many graph neural networks have been developed to learn graph representations in either Euclidean or hyperbolic space, with all nodes' representations embedded in a single space. However, a graph can have hyperbolic and Euclidean geometries at different regions of the graph. Thus, it is sub-optimal to indifferently embed an entire graph into a single space. In this paper, we explore and analyze two notions of local hyperbolicity, describing the underlying local geometry: geometric (Gromov) and model-based, to determine the preferred space of embedding for each node. The two hyperbolicities' distributions are aligned using the Wasserstein metric such that the calculated geometric hyperbolicity guides the choice of the learned model hyperbolicity. As such our model Joint Space Graph Neural Network (JSGNN) can leverage both Euclidean and hyperbolic spaces during learning by allowing node-specific geometry space selection. We evaluate our model on both node classification and link prediction tasks and observe promising performance compared to baseline models.

On semi shift invariant graph filters

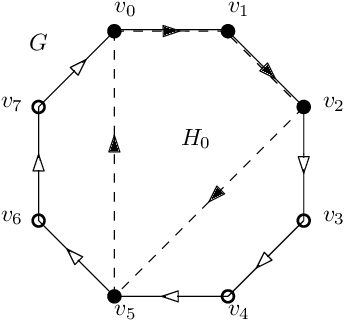
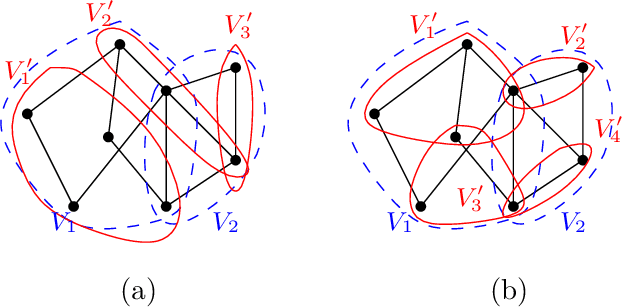
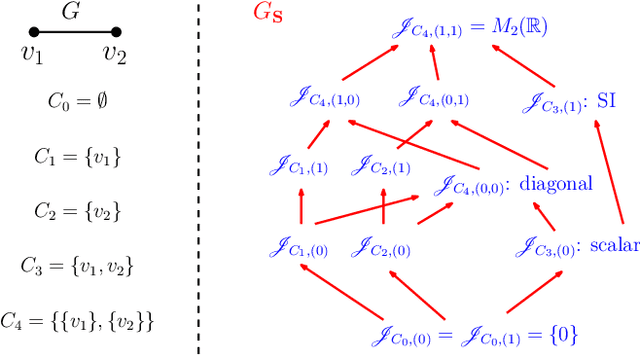
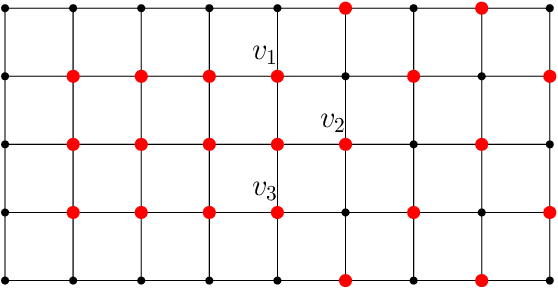
In graph signal processing, one of the most important subjects is the study of filters, i.e., linear transformations that capture relations between graph signals. One of the most important families of filters is the space of shift invariant filters, defined as transformations commute with a preferred graph shift operator. Shift invariant filters have a wide range of applications in graph signal processing and graph neural networks. A shift invariant filter can be interpreted geometrically as an information aggregation procedure (from local neighborhood), and can be computed easily using matrix multiplication. However, there are still drawbacks to using solely shift invariant filters in applications, such as being restrictively homogeneous. In this paper, we generalize shift invariant filters by introducing and studying semi shift invariant filters. We give an application of semi shift invariant filters with a new signal processing framework, the subgraph signal processing. Moreover, we also demonstrate how semi shift invariant filters can be used in graph neural networks.

SGAT: Simplicial Graph Attention Network

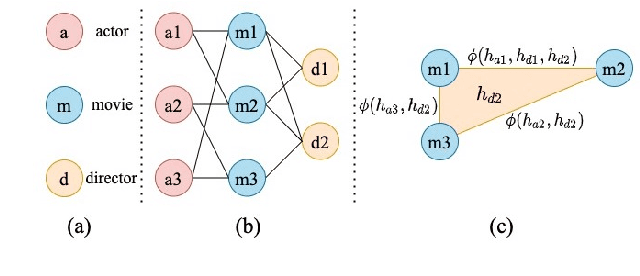
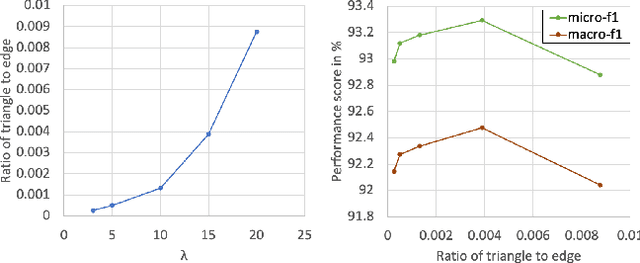
Heterogeneous graphs have multiple node and edge types and are semantically richer than homogeneous graphs. To learn such complex semantics, many graph neural network approaches for heterogeneous graphs use metapaths to capture multi-hop interactions between nodes. Typically, features from non-target nodes are not incorporated into the learning procedure. However, there can be nonlinear, high-order interactions involving multiple nodes or edges. In this paper, we present Simplicial Graph Attention Network (SGAT), a simplicial complex approach to represent such high-order interactions by placing features from non-target nodes on the simplices. We then use attention mechanisms and upper adjacencies to generate representations. We empirically demonstrate the efficacy of our approach with node classification tasks on heterogeneous graph datasets and further show SGAT's ability in extracting structural information by employing random node features. Numerical experiments indicate that SGAT performs better than other current state-of-the-art heterogeneous graph learning methods.

Learning on heterogeneous graphs using high-order relations

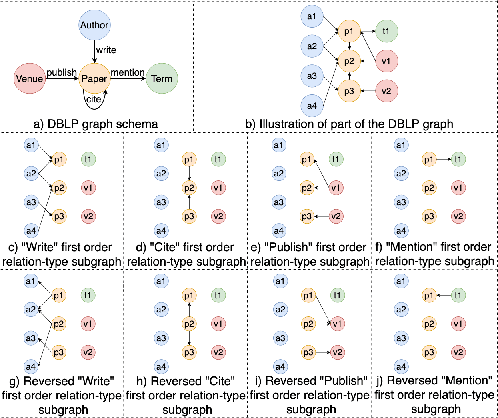
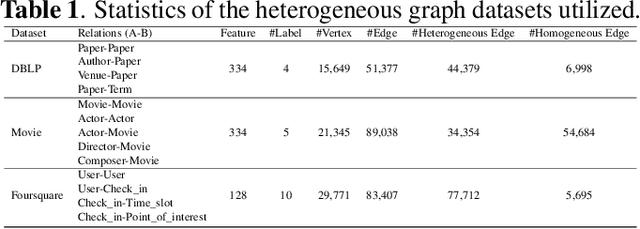
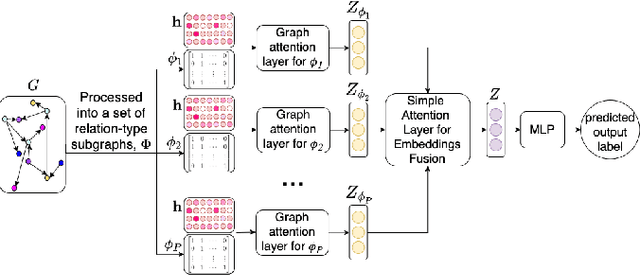
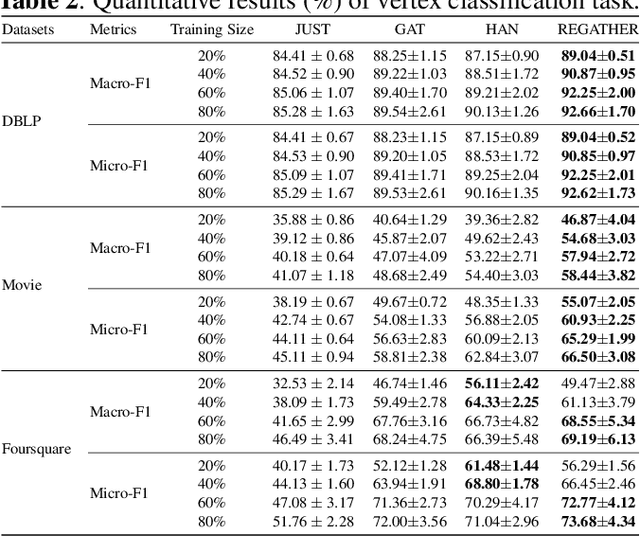
A heterogeneous graph consists of different vertices and edges types. Learning on heterogeneous graphs typically employs meta-paths to deal with the heterogeneity by reducing the graph to a homogeneous network, guide random walks or capture semantics. These methods are however sensitive to the choice of meta-paths, with suboptimal paths leading to poor performance. In this paper, we propose an approach for learning on heterogeneous graphs without using meta-paths. Specifically, we decompose a heterogeneous graph into different homogeneous relation-type graphs, which are then combined to create higher-order relation-type representations. These representations preserve the heterogeneity of edges and retain their edge directions while capturing the interaction of different vertex types multiple hops apart. This is then complemented with attention mechanisms to distinguish the importance of the relation-type based neighbors and the relation-types themselves. Experiments demonstrate that our model generally outperforms other state-of-the-art baselines in the vertex classification task on three commonly studied heterogeneous graph datasets.