On semi shift invariant graph filters
Paper and Code
Sep 28, 2022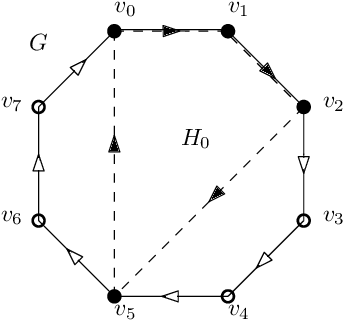
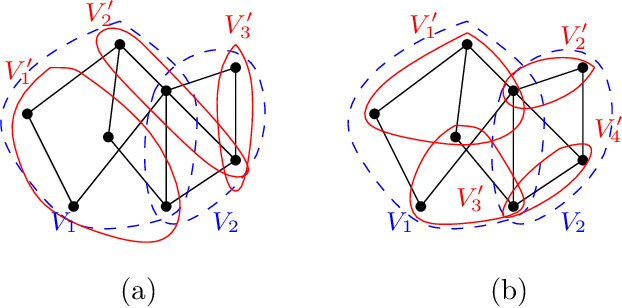
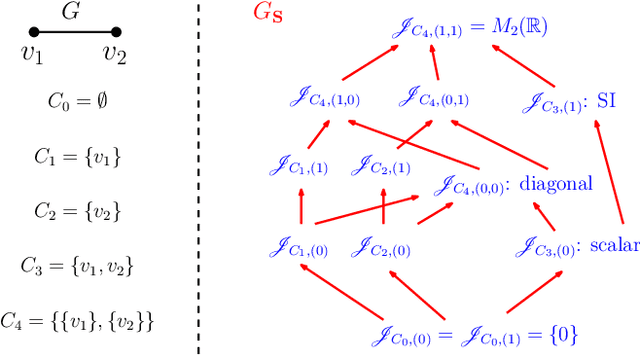
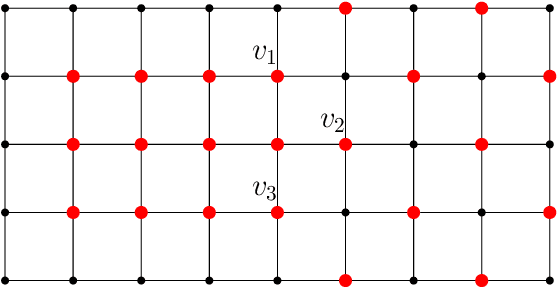
In graph signal processing, one of the most important subjects is the study of filters, i.e., linear transformations that capture relations between graph signals. One of the most important families of filters is the space of shift invariant filters, defined as transformations commute with a preferred graph shift operator. Shift invariant filters have a wide range of applications in graph signal processing and graph neural networks. A shift invariant filter can be interpreted geometrically as an information aggregation procedure (from local neighborhood), and can be computed easily using matrix multiplication. However, there are still drawbacks to using solely shift invariant filters in applications, such as being restrictively homogeneous. In this paper, we generalize shift invariant filters by introducing and studying semi shift invariant filters. We give an application of semi shift invariant filters with a new signal processing framework, the subgraph signal processing. Moreover, we also demonstrate how semi shift invariant filters can be used in graph neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge