Torsion Graph Neural Networks
Paper and Code
Jun 23, 2023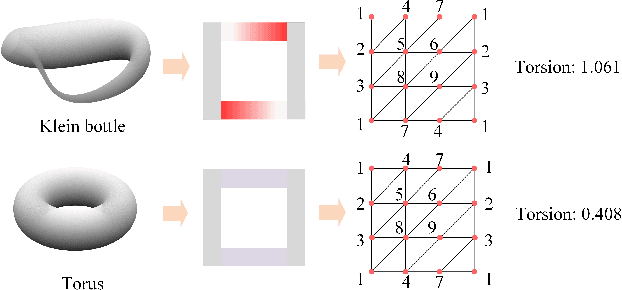
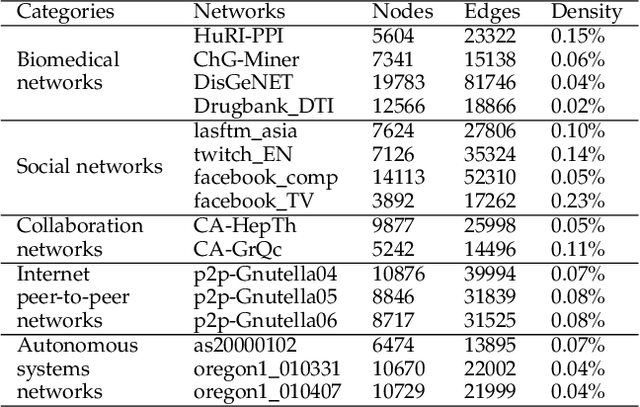
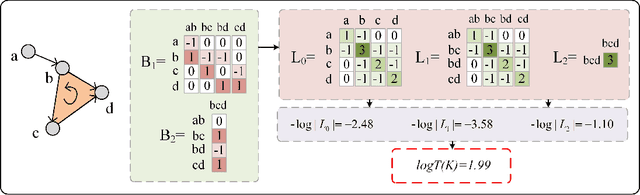

Geometric deep learning (GDL) models have demonstrated a great potential for the analysis of non-Euclidian data. They are developed to incorporate the geometric and topological information of non-Euclidian data into the end-to-end deep learning architectures. Motivated by the recent success of discrete Ricci curvature in graph neural network (GNNs), we propose TorGNN, an analytic Torsion enhanced Graph Neural Network model. The essential idea is to characterize graph local structures with an analytic torsion based weight formula. Mathematically, analytic torsion is a topological invariant that can distinguish spaces which are homotopy equivalent but not homeomorphic. In our TorGNN, for each edge, a corresponding local simplicial complex is identified, then the analytic torsion (for this local simplicial complex) is calculated, and further used as a weight (for this edge) in message-passing process. Our TorGNN model is validated on link prediction tasks from sixteen different types of networks and node classification tasks from three types of networks. It has been found that our TorGNN can achieve superior performance on both tasks, and outperform various state-of-the-art models. This demonstrates that analytic torsion is a highly efficient topological invariant in the characterization of graph structures and can significantly boost the performance of GNNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge