Surrogate Modelling for Injection Molding Processes using Machine Learning

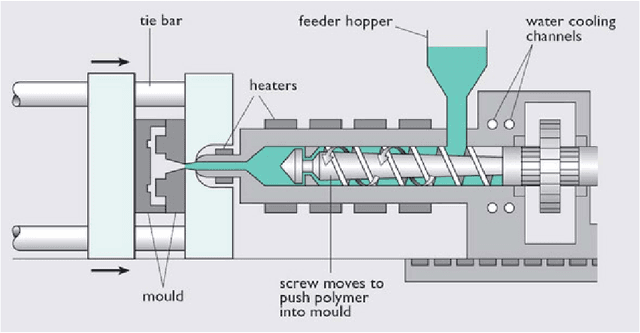
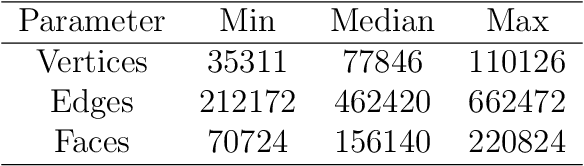
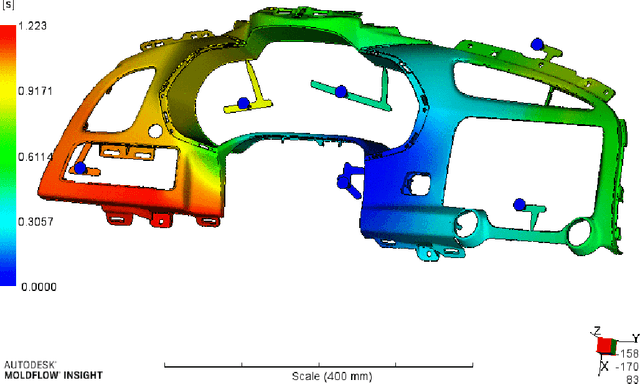
Injection molding is one of the most popular manufacturing methods for the modeling of complex plastic objects. Faster numerical simulation of the technological process would allow for faster and cheaper design cycles of new products. In this work, we propose a baseline for a data processing pipeline that includes the extraction of data from Moldflow simulation projects and the prediction of the fill time and deflection distributions over 3-dimensional surfaces using machine learning models. We propose algorithms for engineering of features, including information of injector gates parameters that will mostly affect the time for plastic to reach the particular point of the form for fill time prediction, and geometrical features for deflection prediction. We propose and evaluate baseline machine learning models for fill time and deflection distribution prediction and provide baseline values of MSE and RMSE metrics. Finally, we measure the execution time of our solution and show that it significantly exceeds the time of simulation with Moldflow software: approximately 17 times and 14 times faster for mean and median total times respectively, comparing the times of all analysis stages for deflection prediction. Our solution has been implemented in a prototype web application that was approved by the management board of Fiat Chrysler Automobiles and Illogic SRL. As one of the promising applications of this surrogate modelling approach, we envision the use of trained models as a fast objective function in the task of optimization of technological parameters of the injection molding process (meaning optimal placement of gates), which could significantly aid engineers in this task, or even automate it.

Kernel Methods on Approximate Infinite-Dimensional Covariance Operators for Image Classification

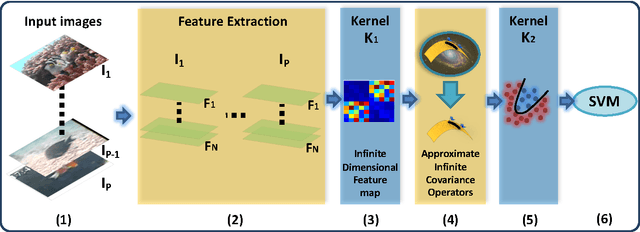
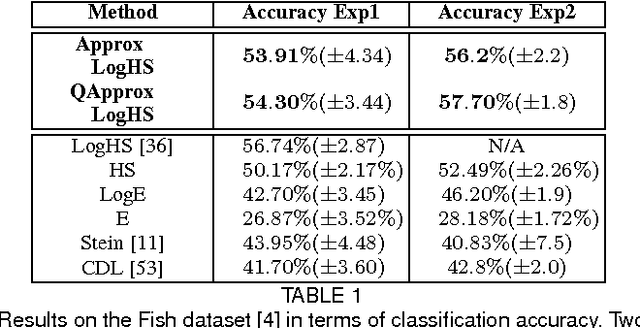
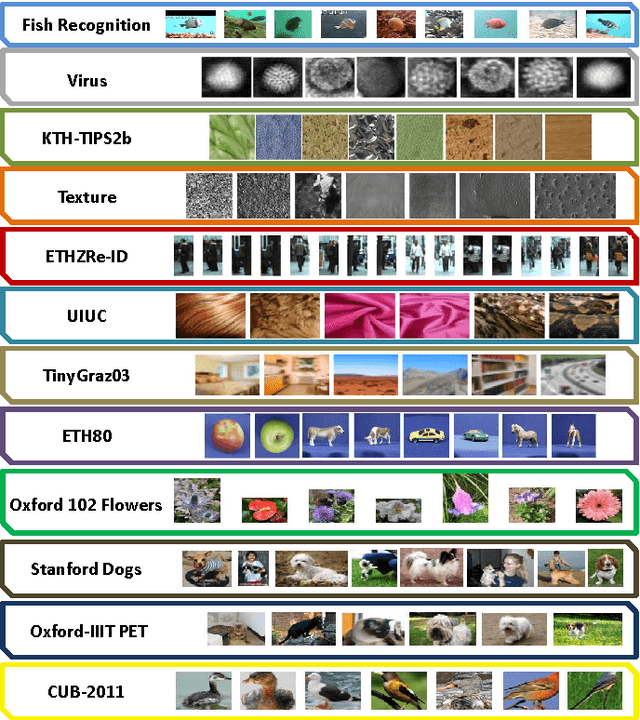
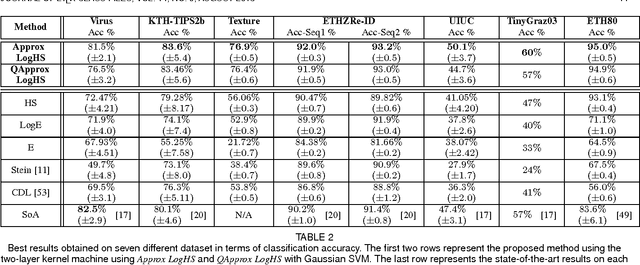
This paper presents a novel framework for visual object recognition using infinite-dimensional covariance operators of input features in the paradigm of kernel methods on infinite-dimensional Riemannian manifolds. Our formulation provides in particular a rich representation of image features by exploiting their non-linear correlations. Theoretically, we provide a finite-dimensional approximation of the Log-Hilbert-Schmidt (Log-HS) distance between covariance operators that is scalable to large datasets, while maintaining an effective discriminating capability. This allows us to efficiently approximate any continuous shift-invariant kernel defined using the Log-HS distance. At the same time, we prove that the Log-HS inner product between covariance operators is only approximable by its finite-dimensional counterpart in a very limited scenario. Consequently, kernels defined using the Log-HS inner product, such as polynomial kernels, are not scalable in the same way as shift-invariant kernels. Computationally, we apply the approximate Log-HS distance formulation to covariance operators of both handcrafted and convolutional features, exploiting both the expressiveness of these features and the power of the covariance representation. Empirically, we tested our framework on the task of image classification on twelve challenging datasets. In almost all cases, the results obtained outperform other state of the art methods, demonstrating the competitiveness and potential of our framework.

Kernelized Covariance for Action Recognition

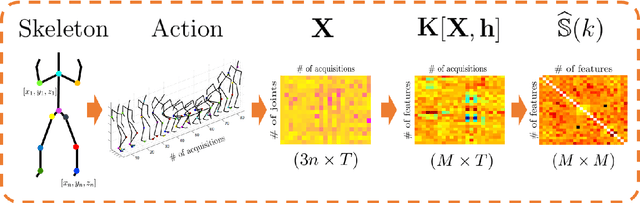
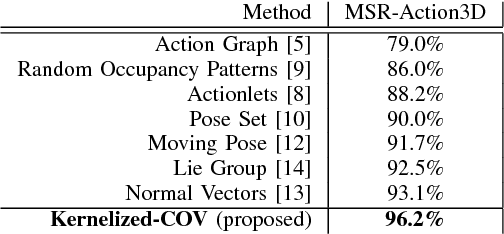
In this paper we aim at increasing the descriptive power of the covariance matrix, limited in capturing linear mutual dependencies between variables only. We present a rigorous and principled mathematical pipeline to recover the kernel trick for computing the covariance matrix, enhancing it to model more complex, non-linear relationships conveyed by the raw data. To this end, we propose Kernelized-COV, which generalizes the original covariance representation without compromising the efficiency of the computation. In the experiments, we validate the proposed framework against many previous approaches in the literature, scoring on par or superior with respect to the state of the art on benchmark datasets for 3D action recognition.