A Formalization of The Natural Gradient Method for General Similarity Measures
Paper and Code
Feb 24, 2019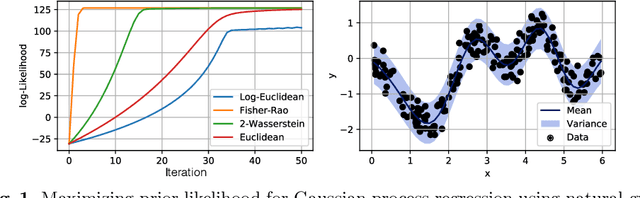
In optimization, the natural gradient method is well-known for likelihood maximization. The method uses the Kullback-Leibler divergence, corresponding infinitesimally to the Fisher-Rao metric, which is pulled back to the parameter space of a family of probability distributions. This way, gradients with respect to the parameters respect the Fisher-Rao geometry of the space of distributions, which might differ vastly from the standard Euclidean geometry of the parameter space, often leading to faster convergence. However, when minimizing an arbitrary similarity measure between distributions, it is generally unclear which metric to use. We provide a general framework that, given a similarity measure, derives a metric for the natural gradient. We then discuss connections between the natural gradient method and multiple other optimization techniques in the literature. Finally, we provide computations of the formal natural gradient to show overlap with well-known cases and to compute natural gradients in novel frameworks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge