Bayesian Inference for Optimal Transport with Stochastic Cost

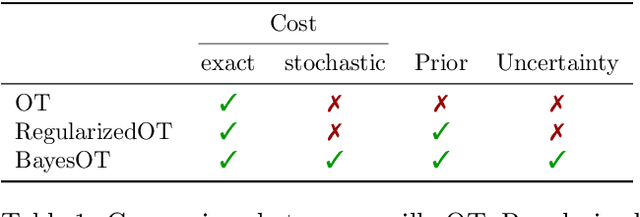
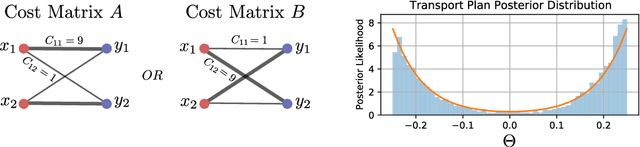
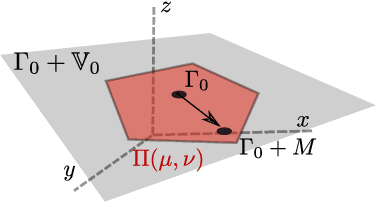
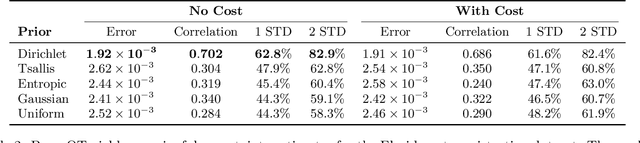
In machine learning and computer vision, optimal transport has had significant success in learning generative models and defining metric distances between structured and stochastic data objects, that can be cast as probability measures. The key element of optimal transport is the so called lifting of an \emph{exact} cost (distance) function, defined on the sample space, to a cost (distance) between probability measures over the sample space. However, in many real life applications the cost is \emph{stochastic}: e.g., the unpredictable traffic flow affects the cost of transportation between a factory and an outlet. To take this stochasticity into account, we introduce a Bayesian framework for inferring the optimal transport plan distribution induced by the stochastic cost, allowing for a principled way to include prior information and to model the induced stochasticity on the transport plans. Additionally, we tailor an HMC method to sample from the resulting transport plan posterior distribution.