Zhengyang Liu
PRIM: Towards Practical In-Image Multilingual Machine Translation
Sep 05, 2025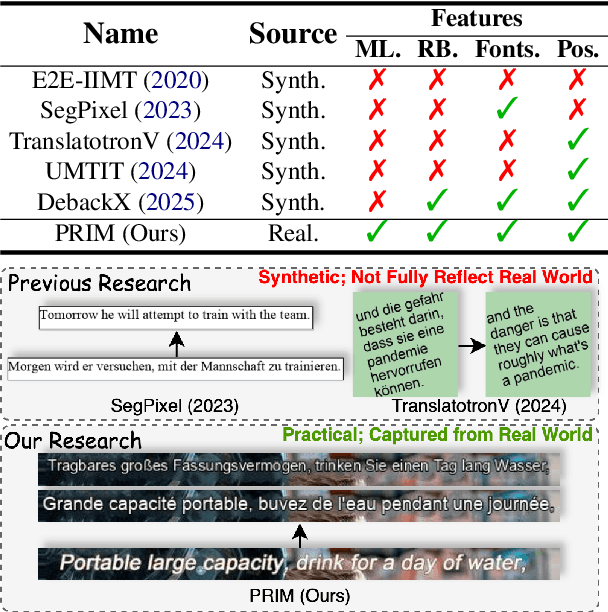
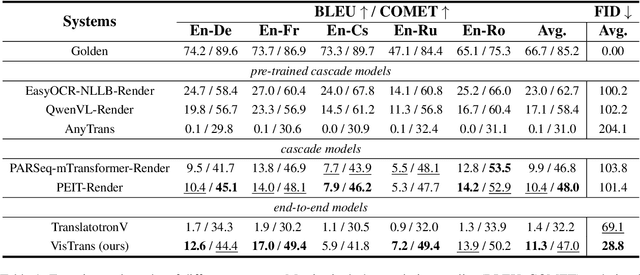
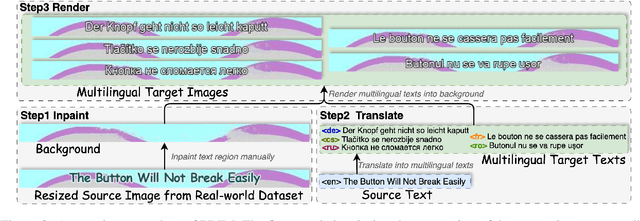

Abstract:In-Image Machine Translation (IIMT) aims to translate images containing texts from one language to another. Current research of end-to-end IIMT mainly conducts on synthetic data, with simple background, single font, fixed text position, and bilingual translation, which can not fully reflect real world, causing a significant gap between the research and practical conditions. To facilitate research of IIMT in real-world scenarios, we explore Practical In-Image Multilingual Machine Translation (IIMMT). In order to convince the lack of publicly available data, we annotate the PRIM dataset, which contains real-world captured one-line text images with complex background, various fonts, diverse text positions, and supports multilingual translation directions. We propose an end-to-end model VisTrans to handle the challenge of practical conditions in PRIM, which processes visual text and background information in the image separately, ensuring the capability of multilingual translation while improving the visual quality. Experimental results indicate the VisTrans achieves a better translation quality and visual effect compared to other models. The code and dataset are available at: https://github.com/BITHLP/PRIM.
Exploring In-Image Machine Translation with Real-World Background
May 21, 2025Abstract:In-Image Machine Translation (IIMT) aims to translate texts within images from one language to another. Previous research on IIMT was primarily conducted on simplified scenarios such as images of one-line text with black font in white backgrounds, which is far from reality and impractical for applications in the real world. To make IIMT research practically valuable, it is essential to consider a complex scenario where the text backgrounds are derived from real-world images. To facilitate research of complex scenario IIMT, we design an IIMT dataset that includes subtitle text with real-world background. However previous IIMT models perform inadequately in complex scenarios. To address the issue, we propose the DebackX model, which separates the background and text-image from the source image, performs translation on text-image directly, and fuses the translated text-image with the background, to generate the target image. Experimental results show that our model achieves improvements in both translation quality and visual effect.
Few-shot Sim2Real Based on High Fidelity Rendering with Force Feedback Teleoperation
Mar 03, 2025Abstract:Teleoperation offers a promising approach to robotic data collection and human-robot interaction. However, existing teleoperation methods for data collection are still limited by efficiency constraints in time and space, and the pipeline for simulation-based data collection remains unclear. The problem is how to enhance task performance while minimizing reliance on real-world data. To address this challenge, we propose a teleoperation pipeline for collecting robotic manipulation data in simulation and training a few-shot sim-to-real visual-motor policy. Force feedback devices are integrated into the teleoperation system to provide precise end-effector gripping force feedback. Experiments across various manipulation tasks demonstrate that force feedback significantly improves both success rates and execution efficiency, particularly in simulation. Furthermore, experiments with different levels of visual rendering quality reveal that enhanced visual realism in simulation substantially boosts task performance while reducing the need for real-world data.
Online Sequential Decision-Making with Unknown Delays
Feb 23, 2024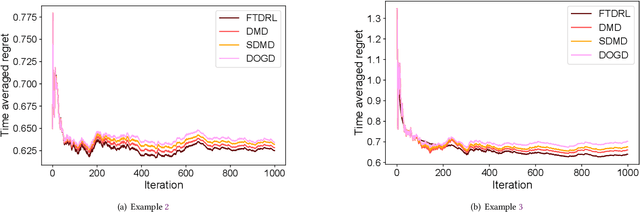
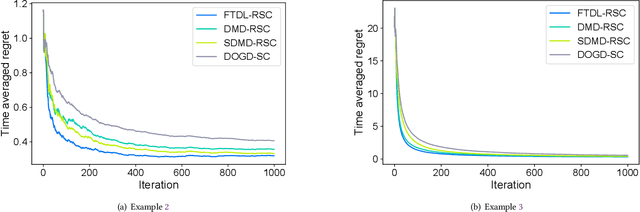
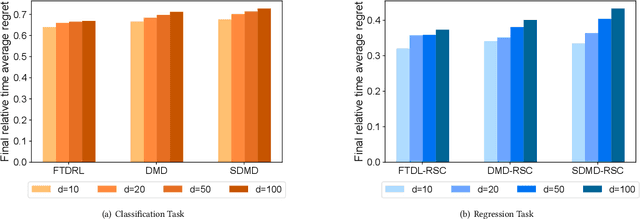
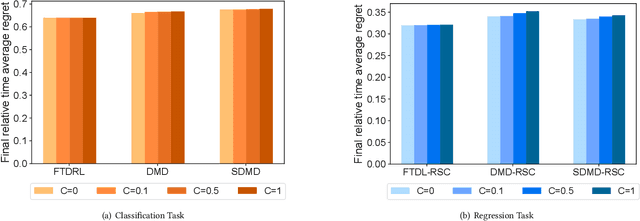
Abstract:In the field of online sequential decision-making, we address the problem with delays utilizing the framework of online convex optimization (OCO), where the feedback of a decision can arrive with an unknown delay. Unlike previous research that is limited to Euclidean norm and gradient information, we propose three families of delayed algorithms based on approximate solutions to handle different types of received feedback. Our proposed algorithms are versatile and applicable to universal norms. Specifically, we introduce a family of Follow the Delayed Regularized Leader algorithms for feedback with full information on the loss function, a family of Delayed Mirror Descent algorithms for feedback with gradient information on the loss function and a family of Simplified Delayed Mirror Descent algorithms for feedback with the value information of the loss function's gradients at corresponding decision points. For each type of algorithm, we provide corresponding regret bounds under cases of general convexity and relative strong convexity, respectively. We also demonstrate the efficiency of each algorithm under different norms through concrete examples. Furthermore, our theoretical results are consistent with the current best bounds when degenerated to standard settings.
ACMo: Angle-Calibrated Moment Methods for Stochastic Optimization
Jun 12, 2020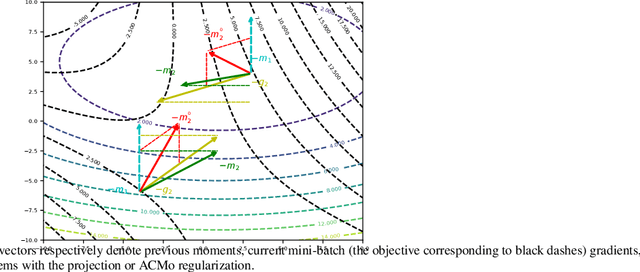

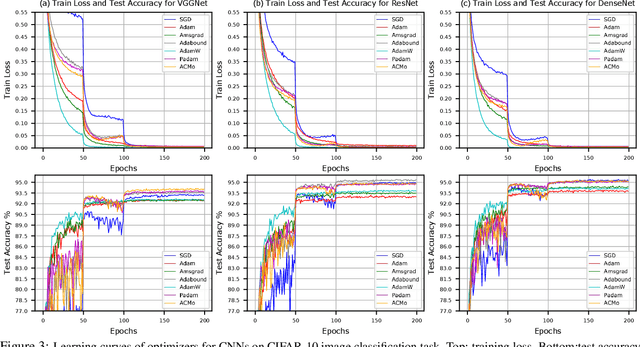
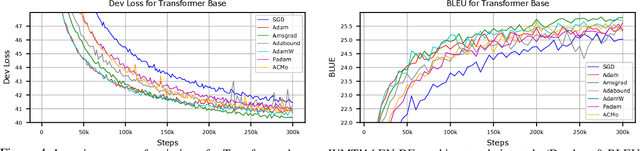
Abstract:Due to its simplicity and outstanding ability to generalize, stochastic gradient descent (SGD) is still the most widely used optimization method despite its slow convergence. Meanwhile, adaptive methods have attracted rising attention of optimization and machine learning communities, both for the leverage of life-long information and for the profound and fundamental mathematical theory. Taking the best of both worlds is the most exciting and challenging question in the field of optimization for machine learning. Along this line, we revisited existing adaptive gradient methods from a novel perspective, refreshing understanding of second moments. Our new perspective empowers us to attach the properties of second moments to the first moment iteration, and to propose a novel first moment optimizer, \emph{Angle-Calibrated Moment method} (\method). Our theoretical results show that \method is able to achieve the same convergence rate as mainstream adaptive methods. Furthermore, extensive experiments on CV and NLP tasks demonstrate that \method has a comparable convergence to SOTA Adam-type optimizers, and gains a better generalization performance in most cases.
SPAN: A Stochastic Projected Approximate Newton Method
Mar 03, 2020
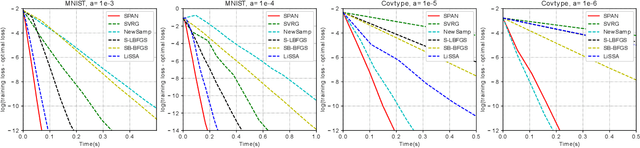
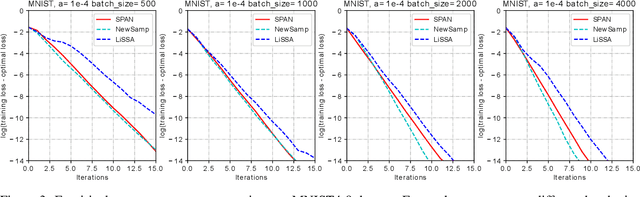
Abstract:Second-order optimization methods have desirable convergence properties. However, the exact Newton method requires expensive computation for the Hessian and its inverse. In this paper, we propose SPAN, a novel approximate and fast Newton method. SPAN computes the inverse of the Hessian matrix via low-rank approximation and stochastic Hessian-vector products. Our experiments on multiple benchmark datasets demonstrate that SPAN outperforms existing first-order and second-order optimization methods in terms of the convergence wall-clock time. Furthermore, we provide a theoretical analysis of the per-iteration complexity, the approximation error, and the convergence rate. Both the theoretical analysis and experimental results show that our proposed method achieves a better trade-off between the convergence rate and the per-iteration efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge