ACMo: Angle-Calibrated Moment Methods for Stochastic Optimization
Paper and Code
Jun 12, 2020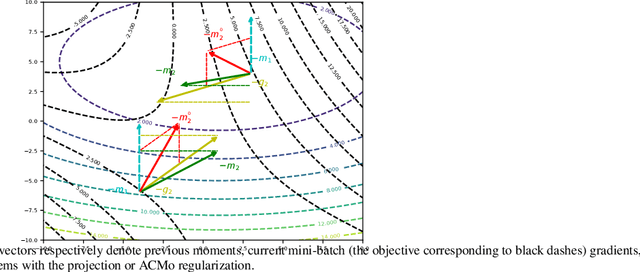

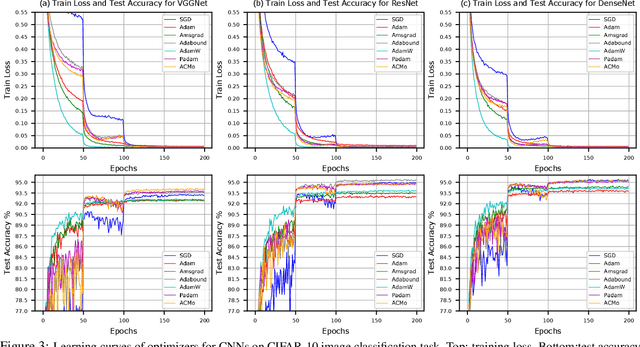
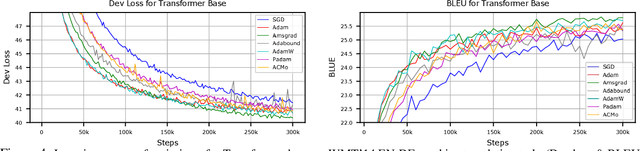
Due to its simplicity and outstanding ability to generalize, stochastic gradient descent (SGD) is still the most widely used optimization method despite its slow convergence. Meanwhile, adaptive methods have attracted rising attention of optimization and machine learning communities, both for the leverage of life-long information and for the profound and fundamental mathematical theory. Taking the best of both worlds is the most exciting and challenging question in the field of optimization for machine learning. Along this line, we revisited existing adaptive gradient methods from a novel perspective, refreshing understanding of second moments. Our new perspective empowers us to attach the properties of second moments to the first moment iteration, and to propose a novel first moment optimizer, \emph{Angle-Calibrated Moment method} (\method). Our theoretical results show that \method is able to achieve the same convergence rate as mainstream adaptive methods. Furthermore, extensive experiments on CV and NLP tasks demonstrate that \method has a comparable convergence to SOTA Adam-type optimizers, and gains a better generalization performance in most cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge