Interest Clock: Time Perception in Real-Time Streaming Recommendation System

User preferences follow a dynamic pattern over a day, e.g., at 8 am, a user might prefer to read news, while at 8 pm, they might prefer to watch movies. Time modeling aims to enable recommendation systems to perceive time changes to capture users' dynamic preferences over time, which is an important and challenging problem in recommendation systems. Especially, streaming recommendation systems in the industry, with only available samples of the current moment, present greater challenges for time modeling. There is still a lack of effective time modeling methods for streaming recommendation systems. In this paper, we propose an effective and universal method Interest Clock to perceive time information in recommendation systems. Interest Clock first encodes users' time-aware preferences into a clock (hour-level personalized features) and then uses Gaussian distribution to smooth and aggregate them into the final interest clock embedding according to the current time for the final prediction. By arming base models with Interest Clock, we conduct online A/B tests, obtaining +0.509% and +0.758% improvements on user active days and app duration respectively. Besides, the extended offline experiments show improvements as well. Interest Clock has been deployed on Douyin Music App.

SPAN: A Stochastic Projected Approximate Newton Method

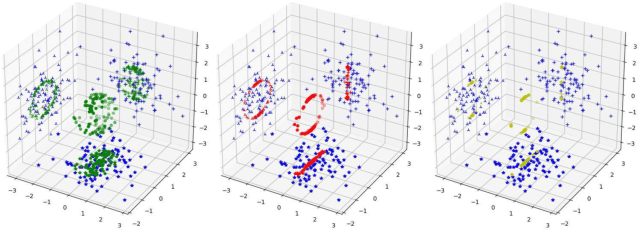
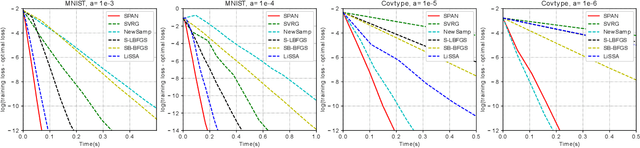
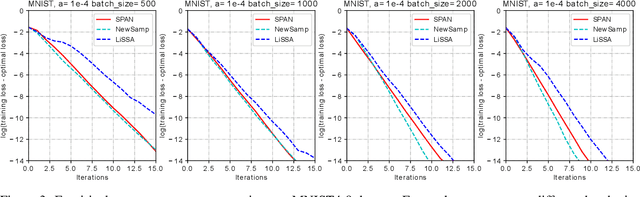
Second-order optimization methods have desirable convergence properties. However, the exact Newton method requires expensive computation for the Hessian and its inverse. In this paper, we propose SPAN, a novel approximate and fast Newton method. SPAN computes the inverse of the Hessian matrix via low-rank approximation and stochastic Hessian-vector products. Our experiments on multiple benchmark datasets demonstrate that SPAN outperforms existing first-order and second-order optimization methods in terms of the convergence wall-clock time. Furthermore, we provide a theoretical analysis of the per-iteration complexity, the approximation error, and the convergence rate. Both the theoretical analysis and experimental results show that our proposed method achieves a better trade-off between the convergence rate and the per-iteration efficiency.

BRITS: Bidirectional Recurrent Imputation for Time Series

Time series are widely used as signals in many classification/regression tasks. It is ubiquitous that time series contains many missing values. Given multiple correlated time series data, how to fill in missing values and to predict their class labels? Existing imputation methods often impose strong assumptions of the underlying data generating process, such as linear dynamics in the state space. In this paper, we propose BRITS, a novel method based on recurrent neural networks for missing value imputation in time series data. Our proposed method directly learns the missing values in a bidirectional recurrent dynamical system, without any specific assumption. The imputed values are treated as variables of RNN graph and can be effectively updated during the backpropagation.BRITS has three advantages: (a) it can handle multiple correlated missing values in time series; (b) it generalizes to time series with nonlinear dynamics underlying; (c) it provides a data-driven imputation procedure and applies to general settings with missing data.We evaluate our model on three real-world datasets, including an air quality dataset, a health-care data, and a localization data for human activity. Experiments show that our model outperforms the state-of-the-art methods in both imputation and classification/regression accuracies.

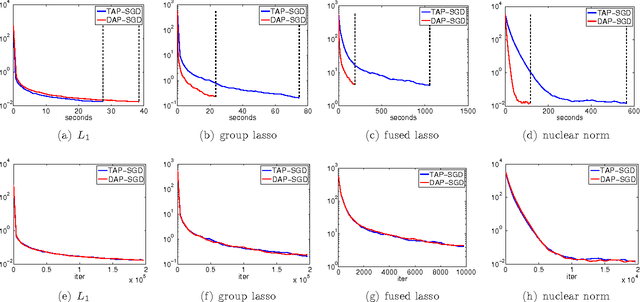
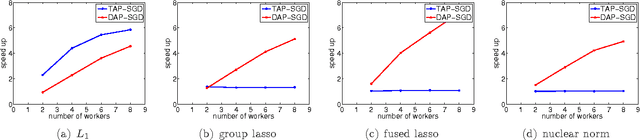
Make Workers Work Harder: Decoupled Asynchronous Proximal Stochastic Gradient Descent

Asynchronous parallel optimization algorithms for solving large-scale machine learning problems have drawn significant attention from academia to industry recently. This paper proposes a novel algorithm, decoupled asynchronous proximal stochastic gradient descent (DAP-SGD), to minimize an objective function that is the composite of the average of multiple empirical losses and a regularization term. Unlike the traditional asynchronous proximal stochastic gradient descent (TAP-SGD) in which the master carries much of the computation load, the proposed algorithm off-loads the majority of computation tasks from the master to workers, and leaves the master to conduct simple addition operations. This strategy yields an easy-to-parallelize algorithm, whose performance is justified by theoretical convergence analyses. To be specific, DAP-SGD achieves an $O(\log T/T)$ rate when the step-size is diminishing and an ergodic $O(1/\sqrt{T})$ rate when the step-size is constant, where $T$ is the number of total iterations.