Xiaowei Zhong
Make Workers Work Harder: Decoupled Asynchronous Proximal Stochastic Gradient Descent
May 21, 2016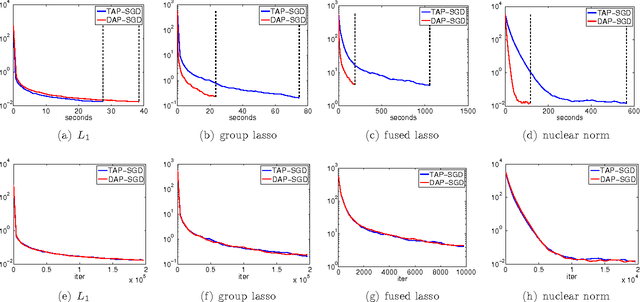
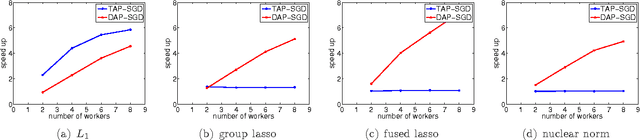
Abstract:Asynchronous parallel optimization algorithms for solving large-scale machine learning problems have drawn significant attention from academia to industry recently. This paper proposes a novel algorithm, decoupled asynchronous proximal stochastic gradient descent (DAP-SGD), to minimize an objective function that is the composite of the average of multiple empirical losses and a regularization term. Unlike the traditional asynchronous proximal stochastic gradient descent (TAP-SGD) in which the master carries much of the computation load, the proposed algorithm off-loads the majority of computation tasks from the master to workers, and leaves the master to conduct simple addition operations. This strategy yields an easy-to-parallelize algorithm, whose performance is justified by theoretical convergence analyses. To be specific, DAP-SGD achieves an $O(\log T/T)$ rate when the step-size is diminishing and an ergodic $O(1/\sqrt{T})$ rate when the step-size is constant, where $T$ is the number of total iterations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge