Yilin Mo
A Control Theory inspired Exploration Method for a Linear Bandit driven by a Linear Gaussian Dynamical System
Oct 01, 2025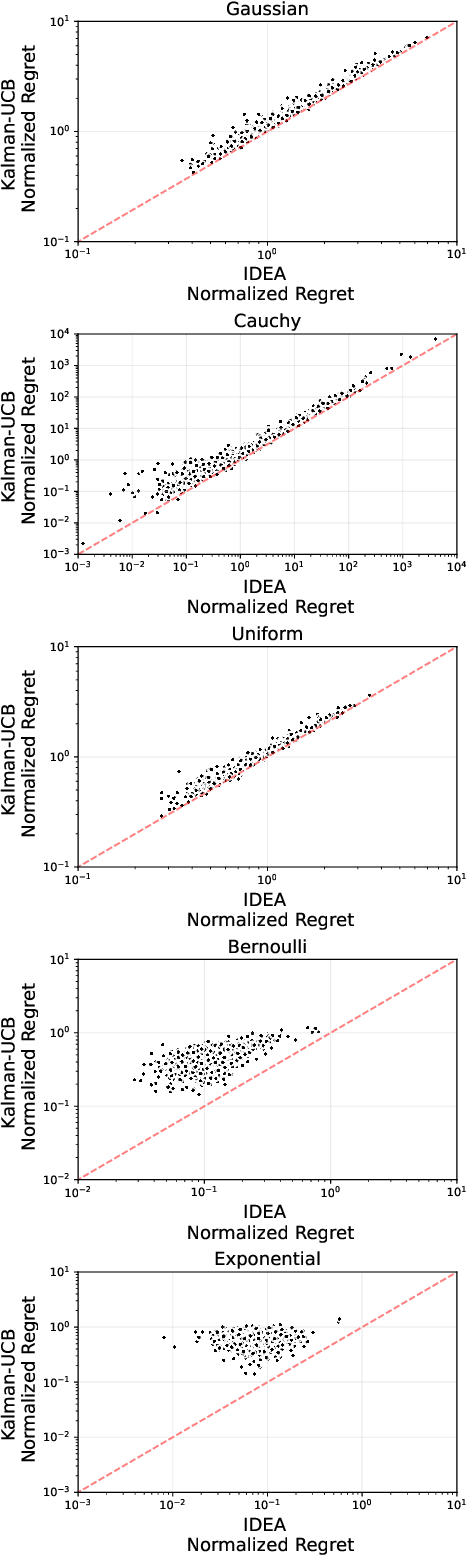
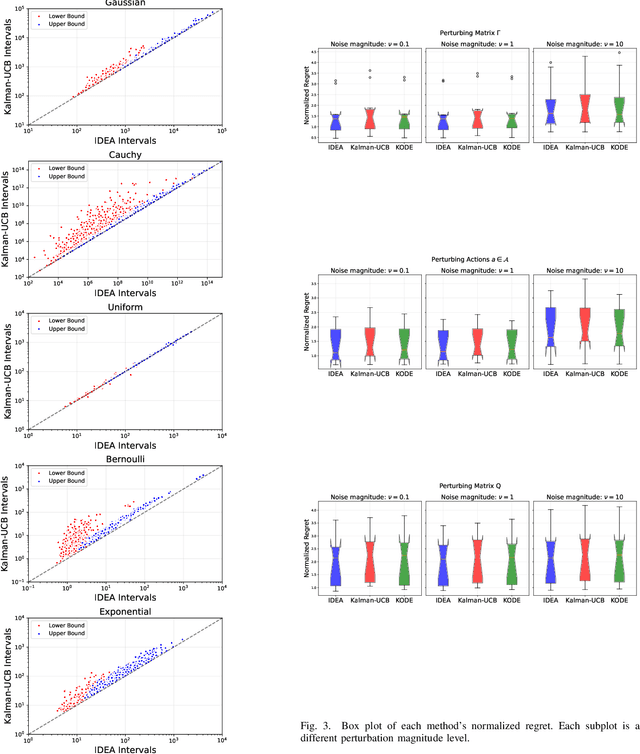
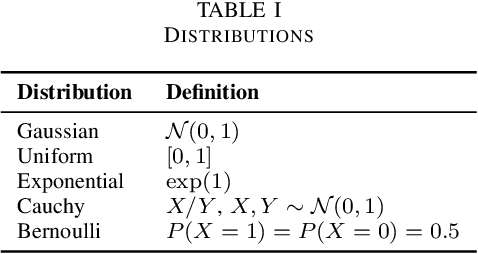
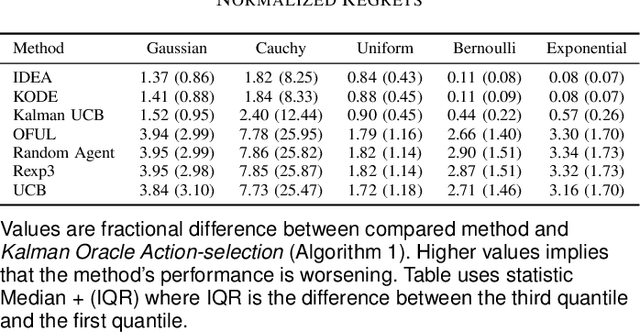
Abstract:The paper introduces a linear bandit environment where the reward is the output of a known Linear Gaussian Dynamical System (LGDS). In this environment, we address the fundamental challenge of balancing exploration -- gathering information about the environment -- and exploitation -- selecting to the action with the highest predicted reward. We propose two algorithms, Kalman filter Upper Confidence Bound (Kalman-UCB) and Information filter Directed Exploration Action-selection (IDEA). Kalman-UCB uses the principle of optimism in the face of uncertainty. IDEA selects actions that maximize the combination of the predicted reward and a term that quantifies how much an action minimizes the error of the Kalman filter state prediction, which depends on the LGDS property called observability. IDEA is motivated by applications such as hyperparameter optimization in machine learning. A major problem encountered in hyperparameter optimization is the large action spaces, which hinder the performance of methods inspired by principle of optimism in the face of uncertainty as they need to explore each action to lower reward prediction uncertainty. To predict if either Kalman-UCB or IDEA will perform better, a metric based on the LGDS properties is provided. This metric is validated with numerical results across a variety of randomly generated environments.
An Exploration-free Method for a Linear Stochastic Bandit Driven by a Linear Gaussian Dynamical System
Apr 04, 2025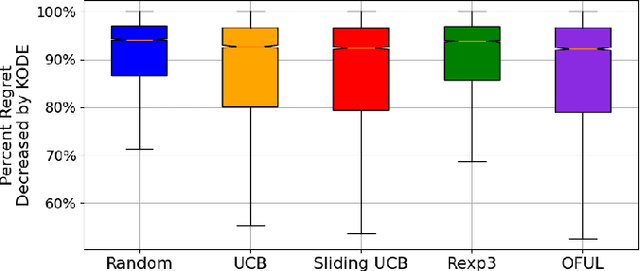
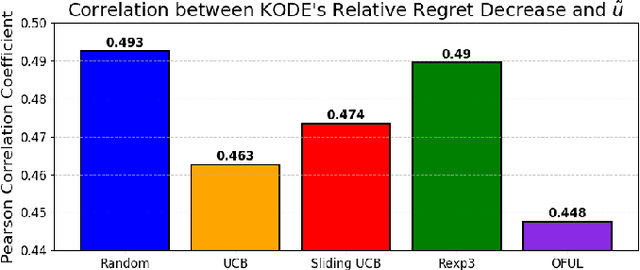
Abstract:In stochastic multi-armed bandits, a major problem the learner faces is the trade-off between exploration and exploitation. Recently, exploration-free methods -- methods that commit to the action predicted to return the highest reward -- have been studied from the perspective of linear bandits. In this paper, we introduce a linear bandit setting where the reward is the output of a linear Gaussian dynamical system. Motivated by a problem encountered in hyperparameter optimization for reinforcement learning, where the number of actions is much higher than the number of training iterations, we propose Kalman filter Observability Dependent Exploration (KODE), an exploration-free method that utilizes the Kalman filter predictions to select actions. Our major contribution of this work is our analysis of the performance of the proposed method, which is dependent on the observability properties of the underlying linear Gaussian dynamical system. We evaluate KODE via two different metrics: regret, which is the cumulative expected difference between the highest possible reward and the reward sampled by KODE, and action alignment, which measures how closely KODE's chosen action aligns with the linear Gaussian dynamical system's state variable. To provide intuition on the performance, we prove that KODE implicitly encourages the learner to explore actions depending on the observability of the linear Gaussian dynamical system. This method is compared to several well-known stochastic multi-armed bandit algorithms to validate our theoretical results.
Bridging the Gaps: Learning Verifiable Model-Free Quadratic Programming Controllers Inspired by Model Predictive Control
Dec 26, 2023



Abstract:In this paper, we introduce a new class of parameterized controllers, drawing inspiration from Model Predictive Control (MPC). The controller resembles a Quadratic Programming (QP) solver of a linear MPC problem, with the parameters of the controller being trained via Deep Reinforcement Learning (DRL) rather than derived from system models. This approach addresses the limitations of common controllers with Multi-Layer Perceptron (MLP) or other general neural network architecture used in DRL, in terms of verifiability and performance guarantees, and the learned controllers possess verifiable properties like persistent feasibility and asymptotic stability akin to MPC. On the other hand, numerical examples illustrate that the proposed controller empirically matches MPC and MLP controllers in terms of control performance and has superior robustness against modeling uncertainty and noises. Furthermore, the proposed controller is significantly more computationally efficient compared to MPC and requires fewer parameters to learn than MLP controllers. Real-world experiments on vehicle drift maneuvering task demonstrate the potential of these controllers for robotics and other demanding control tasks.
Generalized Activation via Multivariate Projection
Sep 29, 2023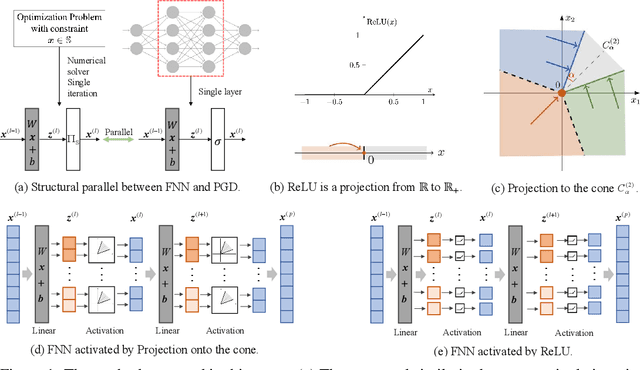
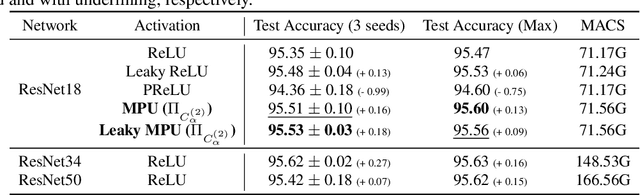
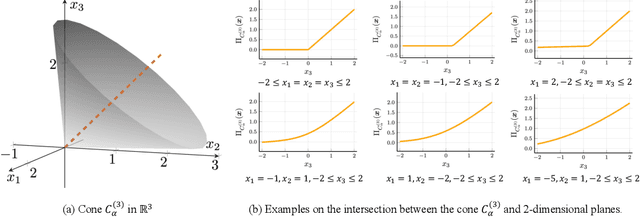
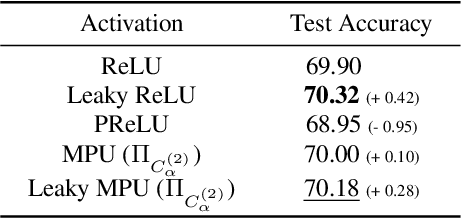
Abstract:Activation functions are essential to introduce nonlinearity into neural networks, with the Rectified Linear Unit (ReLU) often favored for its simplicity and effectiveness. Motivated by the structural similarity between a shallow Feedforward Neural Network (FNN) and a single iteration of the Projected Gradient Descent (PGD) algorithm, a standard approach for solving constrained optimization problems, we consider ReLU as a projection from R onto the nonnegative half-line R+. Building on this interpretation, we extend ReLU by substituting it with a generalized projection operator onto a convex cone, such as the Second-Order Cone (SOC) projection, thereby naturally extending it to a Multivariate Projection Unit (MPU), an activation function with multiple inputs and multiple outputs. We further provide a mathematical proof establishing that FNNs activated by SOC projections outperform those utilizing ReLU in terms of expressive power. Experimental evaluations on widely-adopted architectures further corroborate MPU's effectiveness against a broader range of existing activation functions.
Consecutive Inertia Drift of Autonomous RC Car via Primitive-based Planning and Data-driven Control
Jun 21, 2023



Abstract:Inertia drift is an aggressive transitional driving maneuver, which is challenging due to the high nonlinearity of the system and the stringent requirement on control and planning performance. This paper presents a solution for the consecutive inertia drift of an autonomous RC car based on primitive-based planning and data-driven control. The planner generates complex paths via the concatenation of path segments called primitives, and the controller eases the burden on feedback by interpolating between multiple real trajectories with different initial conditions into one near-feasible reference trajectory. The proposed strategy is capable of drifting through various paths containing consecutive turns, which is validated in both simulation and reality.
Almost Surely $\sqrt{T}$ Regret Bound for Adaptive LQR
Jan 13, 2023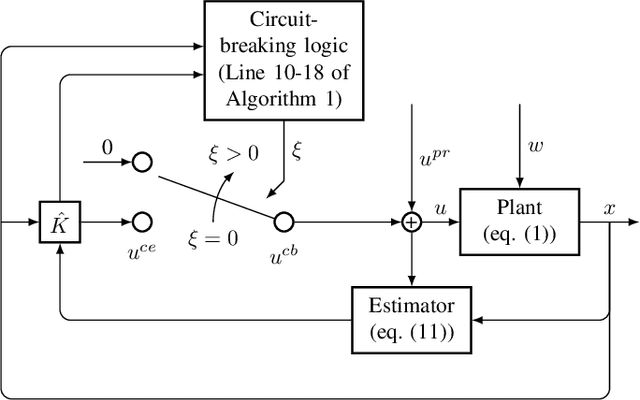
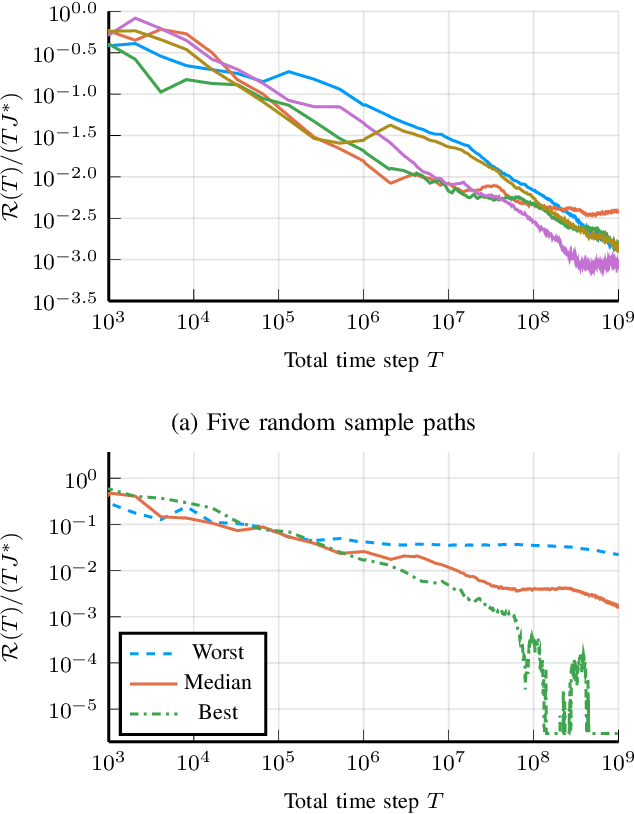
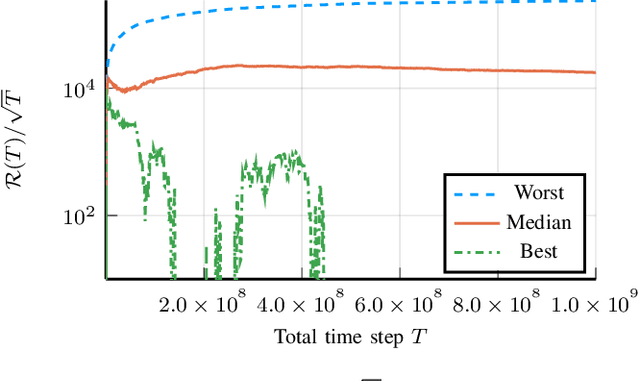
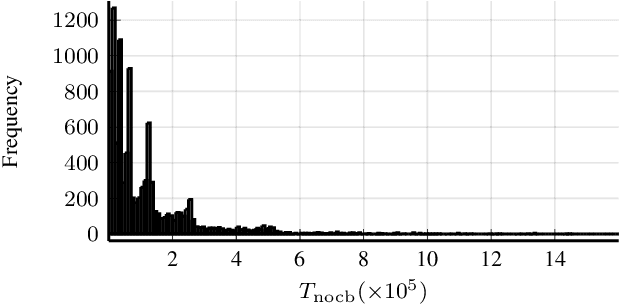
Abstract:The Linear-Quadratic Regulation (LQR) problem with unknown system parameters has been widely studied, but it has remained unclear whether $\tilde{ \mathcal{O}}(\sqrt{T})$ regret, which is the best known dependence on time, can be achieved almost surely. In this paper, we propose an adaptive LQR controller with almost surely $\tilde{ \mathcal{O}}(\sqrt{T})$ regret upper bound. The controller features a circuit-breaking mechanism, which circumvents potential safety breach and guarantees the convergence of the system parameter estimate, but is shown to be triggered only finitely often and hence has negligible effect on the asymptotic performance of the controller. The proposed controller is also validated via simulation on Tennessee Eastman Process~(TEP), a commonly used industrial process example.
Moving Target Interception Considering Dynamic Environment
May 16, 2022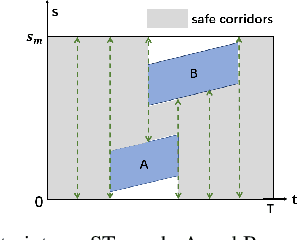

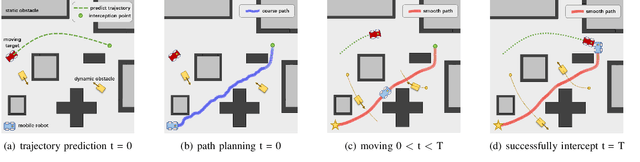
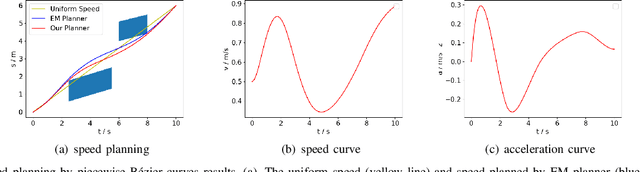
Abstract:The interception of moving targets is a widely studied issue. In this paper, we propose an algorithm of intercepting the moving target with a wheeled mobile robot in a dynamic environment. We first predict the future position of the target through polynomial fitting. The algorithm then generates an interception trajectory with path and speed decoupling. We use Hybrid A* search to plan a path and optimize it via gradient decent method. To avoid the dynamic obstacles in the environment, we introduce ST graph for speed planning. The speed curve is represented by piecewise B\'ezier curves for further optimization. Compared with other interception algorithms, we consider a dynamic environment and plan a safety trajectory which satisfies the kinematic characteristics of the wheeled robot while ensuring the accuracy of interception. Simulation illustrates that the algorithm successfully achieves the interception tasks and has high computational efficiency.
Aggressive Racecar Drifting Control Using Onboard Cameras and Inertial Measurement Unit
Feb 28, 2022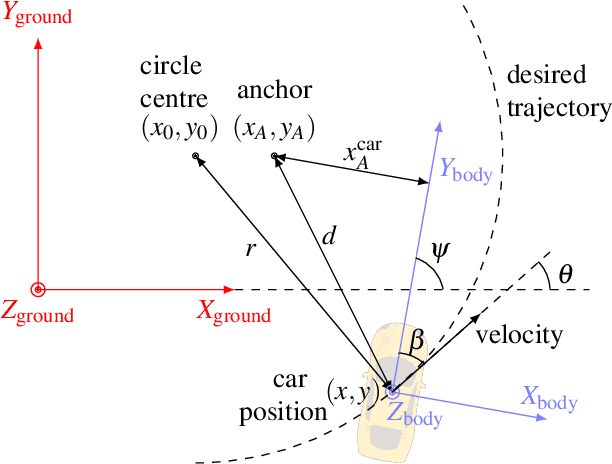
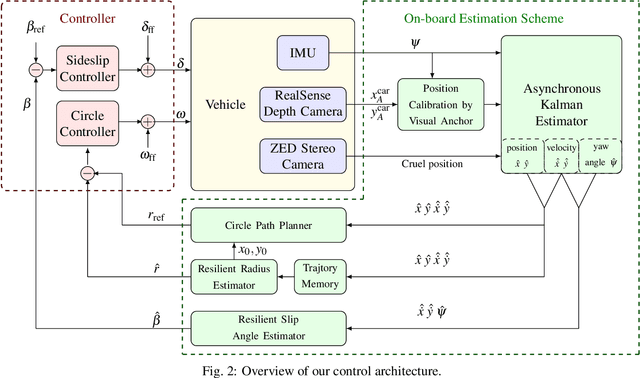
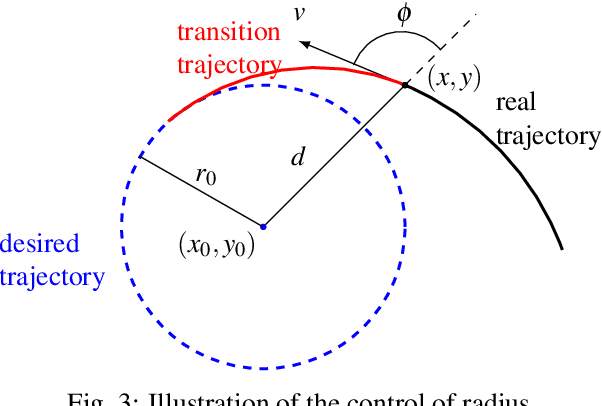

Abstract:Complex autonomous driving, such as drifting, requires high-precision and high-frequency pose information to ensure accuracy and safety, which is notably difficult when using only onboard sensors. In this paper, we propose a drift controller with two feedback control loops: sideslip controller that stabilizes the sideslip angle by tuning the front wheel steering angle, and circle controller that maintains a stable trajectory radius and circle center by controlling the wheel rotational speed. We use an extended Kalman filter to estimate the state. A robustified KASA algorithm is further proposed to accurately estimate the parameters of the circle (i.e., the center and radius) that best fits into the current trajectory. On the premise of the uniform circular motion of the vehicle in the process of stable drift, we use angle information instead of acceleration to describe the dynamic of the vehicle. We implement our method on a 1/10 scale race car. The car drifts stably with a given center and radius, which illustrates the effectiveness of our method.
A Hierarchical Control Framework for Drift Maneuvering of Autonomous Vehicles
Sep 14, 2021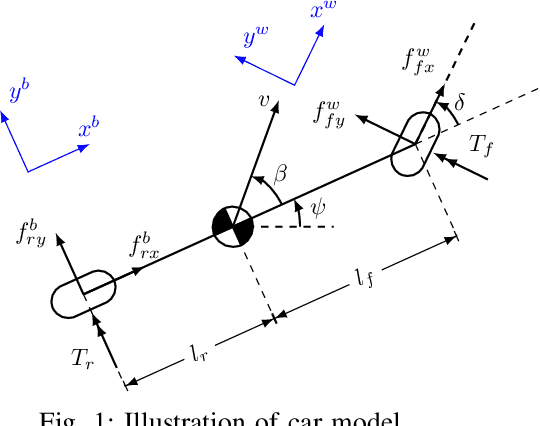
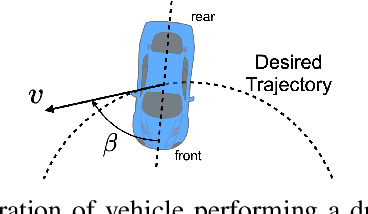
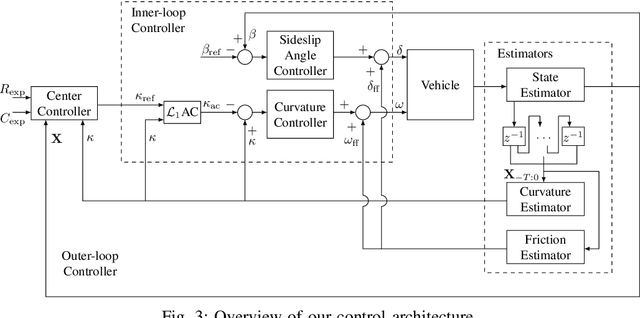
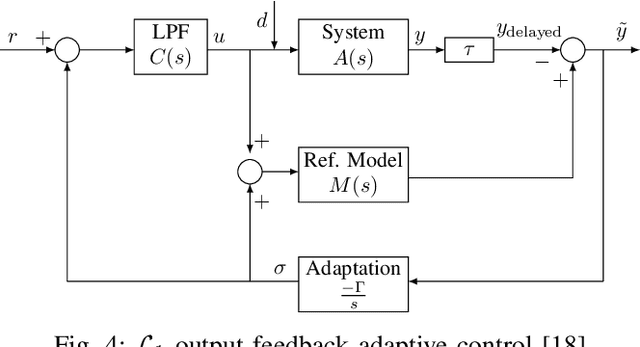
Abstract:Drift control is significant to the safety of autonomous vehicles when there is a sudden loss of traction due to external conditions such as rain or snow. It is a challenging control problem due to the presence of significant sideslip and nearly full saturation of the tires. In this paper, we focus on the control of drift maneuvers following circular paths with either fixed or moving centers, subject to change in the tire-ground interaction, which are common training tasks for drift enthusiasts and can therefore be used as benchmarks of the performance of drift control. In order to achieve the above tasks, we propose a novel hierarchical control architecture which decouples the curvature and center control of the trajectory. In particular, an outer loop stabilizes the center by tuning the target curvature, and an inner loop tracks the curvature using a feedforward/feedback controller enhanced by an $\mathcal{L}_1$ adaptive component. The hierarchical architecture is flexible because the inner loop is task-agnostic and adaptive to changes in tire-road interaction, which allows the outer loop to be designed independent of low-level dynamics, opening up the possibility of incorporating sophisticated planning algorithms. We implement our control strategy on a simulation platform as well as on a 1/10 scale Radio-Control~(RC) car, and both the simulation and experiment results illustrate the effectiveness of our strategy in achieving the above described set of drift maneuvering tasks.
Two-timescale Mechanism-and-Data-Driven Control for Aggressive Driving of Autonomous Cars
Sep 11, 2021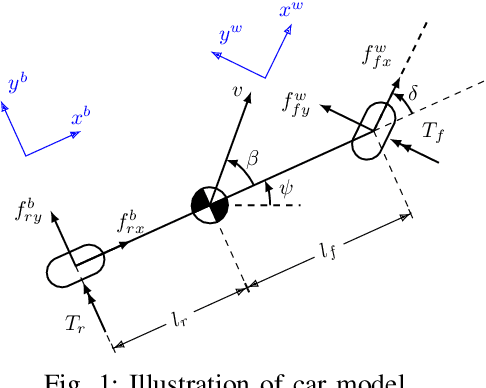
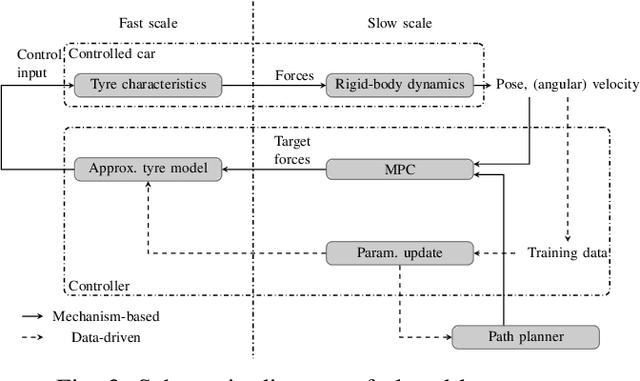
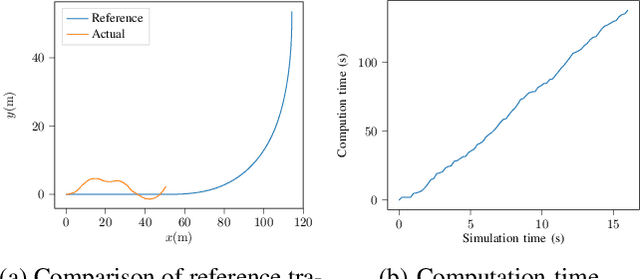

Abstract:The control for aggressive driving of autonomous cars is challenging due to the presence of significant tyre slip. Data-driven and mechanism-based methods for the modeling and control of autonomous cars under aggressive driving conditions are limited in data efficiency and adaptability respectively. This paper is an attempt toward the fusion of the two classes of methods. By means of a modular design that is consisted of mechanism-based and data-driven components, and aware of the two-timescale phenomenon in the car model, our approach effectively improves over previous methods in terms of data efficiency, ability of transfer and final performance. The hybrid mechanism-and-data-driven approach is verified on TORCS (The Open Racing Car Simulator). Experiment results demonstrate the benefit of our approach over purely mechanism-based and purely data-driven methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge