An Exploration-free Method for a Linear Stochastic Bandit Driven by a Linear Gaussian Dynamical System

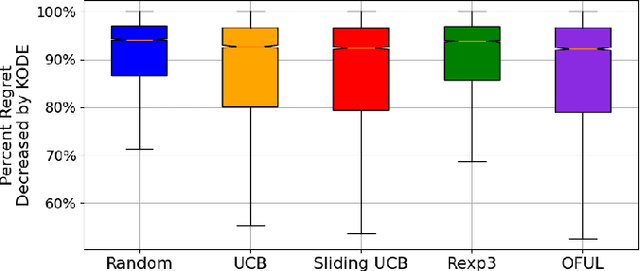
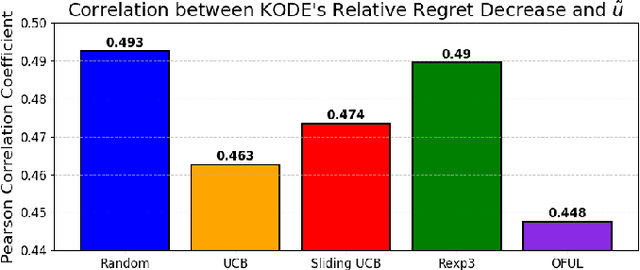
In stochastic multi-armed bandits, a major problem the learner faces is the trade-off between exploration and exploitation. Recently, exploration-free methods -- methods that commit to the action predicted to return the highest reward -- have been studied from the perspective of linear bandits. In this paper, we introduce a linear bandit setting where the reward is the output of a linear Gaussian dynamical system. Motivated by a problem encountered in hyperparameter optimization for reinforcement learning, where the number of actions is much higher than the number of training iterations, we propose Kalman filter Observability Dependent Exploration (KODE), an exploration-free method that utilizes the Kalman filter predictions to select actions. Our major contribution of this work is our analysis of the performance of the proposed method, which is dependent on the observability properties of the underlying linear Gaussian dynamical system. We evaluate KODE via two different metrics: regret, which is the cumulative expected difference between the highest possible reward and the reward sampled by KODE, and action alignment, which measures how closely KODE's chosen action aligns with the linear Gaussian dynamical system's state variable. To provide intuition on the performance, we prove that KODE implicitly encourages the learner to explore actions depending on the observability of the linear Gaussian dynamical system. This method is compared to several well-known stochastic multi-armed bandit algorithms to validate our theoretical results.

Restless Bandit Problem with Rewards Generated by a Linear Gaussian Dynamical System

The stochastic multi-armed bandit problem studies decision-making under uncertainty. In the problem, the learner interacts with an environment by choosing an action at each round, where a round is an instance of an interaction. In response, the environment reveals a reward, which is sampled from a stochastic process, to the learner. The goal of the learner is to maximize cumulative reward. A specific variation of the stochastic multi-armed bandit problem is the restless bandit, where the reward for each action is sampled from a Markov chain. The restless bandit with a discrete state-space is a well-studied problem, but to the best of our knowledge, not many results exist for the continuous state-space version which has many applications such as hyperparameter optimization. In this work, we tackle the restless bandit with continuous state-space by assuming the rewards are the inner product of an action vector and a state vector generated by a linear Gaussian dynamical system. To predict the reward for each action, we propose a method that takes a linear combination of previously observed rewards for predicting each action's next reward. We show that, regardless of the sequence of previous actions chosen, the reward sampled for any previously chosen action can be used for predicting another action's future reward, i.e. the reward sampled for action 1 at round $t-1$ can be used for predicting the reward for action $2$ at round $t$. This is accomplished by designing a modified Kalman filter with a matrix representation that can be learned for reward prediction. Numerical evaluations are carried out on a set of linear Gaussian dynamical systems.

Two Measure is Two Know: Calibration-free Full Duplex Monitoring for Software Radio Platforms

Future virtualized radio access network (vRAN) infrastructure providers (and today's experimental wireless testbed providers) may be simultaneously uncertain what signals are being transmitted by their base stations and legally responsible for their violations. These providers must monitor the spectrum of transmissions and external signals without access to the radio itself. In this paper, we propose FDMonitor, a full-duplex monitoring system attached between a transmitter and its antenna to achieve this goal. Measuring the signal at this point on the RF path is necessary but insufficient since the antenna is a bidirectional device. FDMonitor thus uses a bidirectional coupler, a two-channel receiver, and a new source separation algorithm to simultaneously estimate the transmitted signal and the signal incident on the antenna. Rather than requiring an offline calibration, we also adaptively estimate the linear model for the system on the fly. FDMonitor has been running on a real-world open wireless testbed, monitoring 19 SDR platforms controlled (with bare metal access) by outside experimenters over a seven month period, sending alerts whenever a violation is observed. Our experimental results show that FDMonitor accurately separates signals across a range of signal parameters. Over more than 7 months of observation, it achieves a positive predictive value of 97%, with a total of 20 false alerts.

Stochastic Multi-armed Bandits with Non-stationary Rewards Generated by a Linear Dynamical System

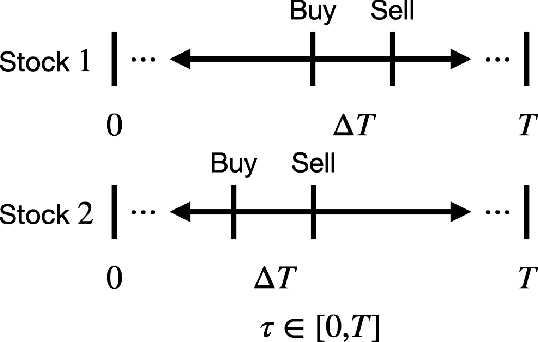
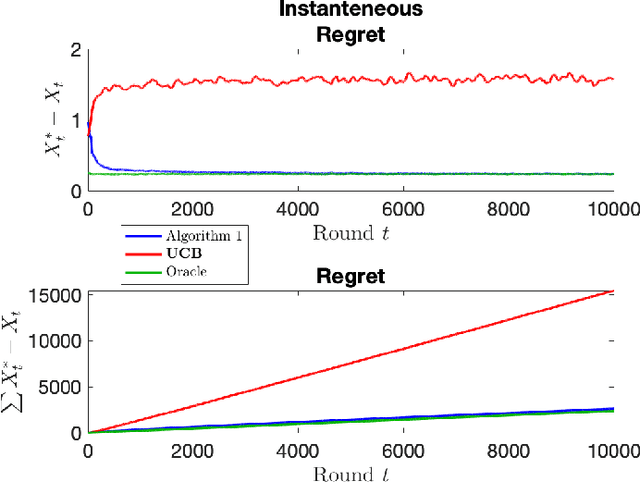
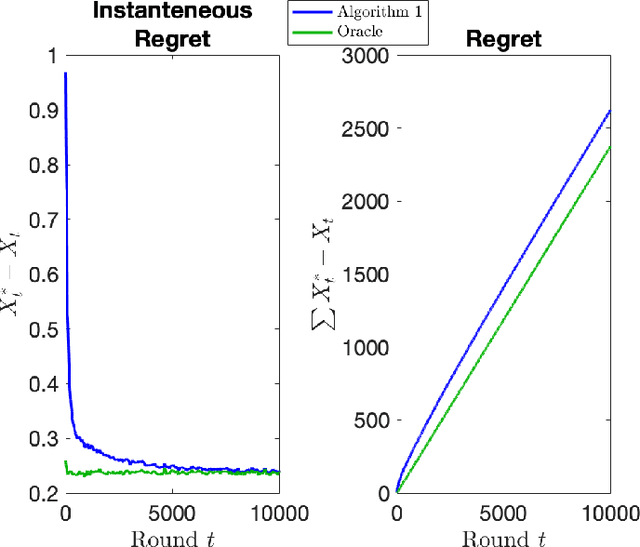
The stochastic multi-armed bandit has provided a framework for studying decision-making in unknown environments. We propose a variant of the stochastic multi-armed bandit where the rewards are sampled from a stochastic linear dynamical system. The proposed strategy for this stochastic multi-armed bandit variant is to learn a model of the dynamical system while choosing the optimal action based on the learned model. Motivated by mathematical finance areas such as Intertemporal Capital Asset Pricing Model proposed by Merton and Stochastic Portfolio Theory proposed by Fernholz that both model asset returns with stochastic differential equations, this strategy is applied to quantitative finance as a high-frequency trading strategy, where the goal is to maximize returns within a time period.