Stochastic Multi-armed Bandits with Non-stationary Rewards Generated by a Linear Dynamical System
Paper and Code
Apr 06, 2022
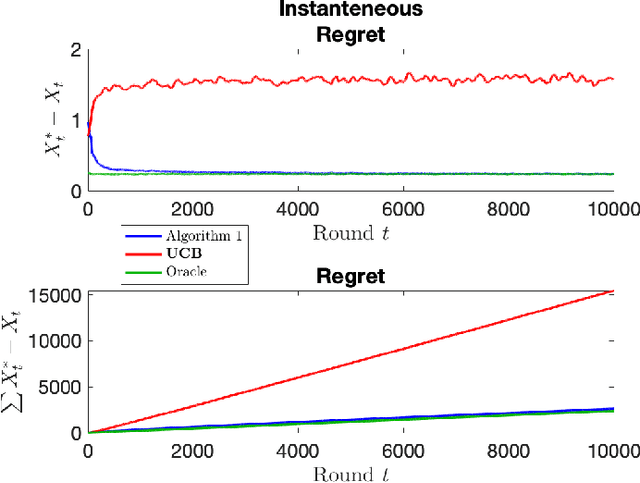
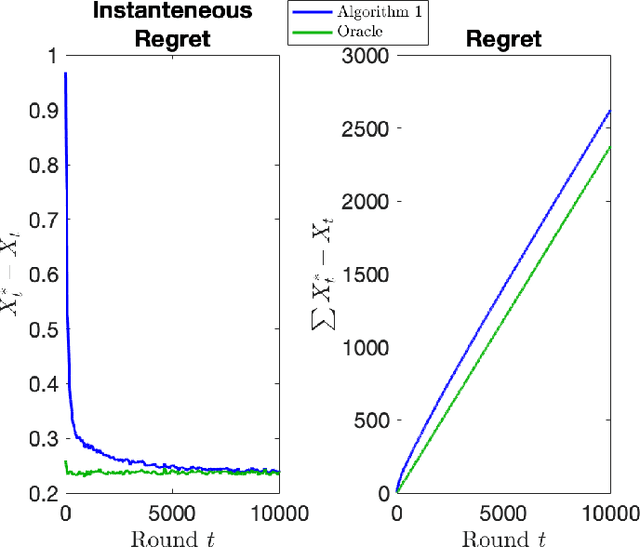
The stochastic multi-armed bandit has provided a framework for studying decision-making in unknown environments. We propose a variant of the stochastic multi-armed bandit where the rewards are sampled from a stochastic linear dynamical system. The proposed strategy for this stochastic multi-armed bandit variant is to learn a model of the dynamical system while choosing the optimal action based on the learned model. Motivated by mathematical finance areas such as Intertemporal Capital Asset Pricing Model proposed by Merton and Stochastic Portfolio Theory proposed by Fernholz that both model asset returns with stochastic differential equations, this strategy is applied to quantitative finance as a high-frequency trading strategy, where the goal is to maximize returns within a time period.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge