An Exploration-free Method for a Linear Stochastic Bandit Driven by a Linear Gaussian Dynamical System

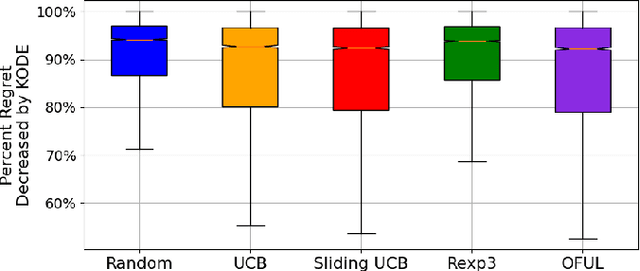
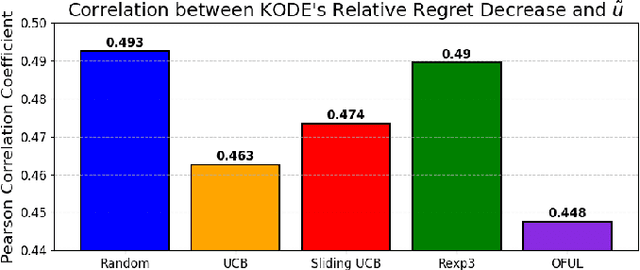
In stochastic multi-armed bandits, a major problem the learner faces is the trade-off between exploration and exploitation. Recently, exploration-free methods -- methods that commit to the action predicted to return the highest reward -- have been studied from the perspective of linear bandits. In this paper, we introduce a linear bandit setting where the reward is the output of a linear Gaussian dynamical system. Motivated by a problem encountered in hyperparameter optimization for reinforcement learning, where the number of actions is much higher than the number of training iterations, we propose Kalman filter Observability Dependent Exploration (KODE), an exploration-free method that utilizes the Kalman filter predictions to select actions. Our major contribution of this work is our analysis of the performance of the proposed method, which is dependent on the observability properties of the underlying linear Gaussian dynamical system. We evaluate KODE via two different metrics: regret, which is the cumulative expected difference between the highest possible reward and the reward sampled by KODE, and action alignment, which measures how closely KODE's chosen action aligns with the linear Gaussian dynamical system's state variable. To provide intuition on the performance, we prove that KODE implicitly encourages the learner to explore actions depending on the observability of the linear Gaussian dynamical system. This method is compared to several well-known stochastic multi-armed bandit algorithms to validate our theoretical results.