Causally-informed Deep Learning towards Explainable and Generalizable Outcomes Prediction in Critical Care

Recent advances in deep learning (DL) have prompted the development of high-performing early warning score (EWS) systems, predicting clinical deteriorations such as acute kidney injury, acute myocardial infarction, or circulatory failure. DL models have proven to be powerful tools for various tasks but come with the cost of lacking interpretability and limited generalizability, hindering their clinical applications. To develop a practical EWS system applicable to various outcomes, we propose causally-informed explainable early prediction model, which leverages causal discovery to identify the underlying causal relationships of prediction and thus owns two unique advantages: demonstrating the explicit interpretation of the prediction while exhibiting decent performance when applied to unfamiliar environments. Benefiting from these features, our approach achieves superior accuracy for 6 different critical deteriorations and achieves better generalizability across different patient groups, compared to various baseline algorithms. Besides, we provide explicit causal pathways to serve as references for assistant clinical diagnosis and potential interventions. The proposed approach enhances the practical application of deep learning in various medical scenarios.

A Compact Implicit Neural Representation for Efficient Storage of Massive 4D Functional Magnetic Resonance Imaging

Functional Magnetic Resonance Imaging (fMRI) data is a kind of widely used four-dimensional biomedical data, demanding effective compression but presenting unique challenges for compression due to its intricate temporal dynamics, low signal-to-noise ratio, and complicated underlying redundancies. This paper reports a novel compression paradigm specifically tailored for fMRI data based on Implicit Neural Representation (INR). The proposed approach focuses on removing the various redundancies among the time series, including (i) conducting spatial correlation modeling for intra-region dynamics, (ii) decomposing reusable neuronal activation patterns, and using proper initialization together with nonlinear fusion to describe the inter-region similarity. The above scheme properly incorporates the unique features of fMRI data, and experimental results on publicly available datasets demonstrate the effectiveness of the proposed method, surpassing state-of-the-art algorithms in both conventional image quality evaluation metrics and fMRI downstream tasks. This work in this paper paves the way for sharing massive fMRI data at low bandwidth and high fidelity.

Lightweight High-Speed Photography Built on Coded Exposure and Implicit Neural Representation of Videos

The compact cameras recording high-speed scenes with high resolution are highly demanded, but the required high bandwidth often leads to bulky, heavy systems, which limits their applications on low-capacity platforms. Adopting a coded exposure setup to encode a frame sequence into a blurry snapshot and retrieve the latent sharp video afterward can serve as a lightweight solution. However, restoring motion from blur is quite challenging due to the high ill-posedness of motion blur decomposition, intrinsic ambiguity in motion direction, and diverse motions in natural videos. In this work, by leveraging classical coded exposure imaging technique and emerging implicit neural representation for videos, we tactfully embed the motion direction cues into the blurry image during the imaging process and develop a novel self-recursive neural network to sequentially retrieve the latent video sequence from the blurry image utilizing the embedded motion direction cues. To validate the effectiveness and efficiency of the proposed framework, we conduct extensive experiments on benchmark datasets and real-captured blurry images. The results demonstrate that our proposed framework significantly outperforms existing methods in quality and flexibility. The code for our work is available at https://github.com/zhihongz/BDINR

CausalTime: Realistically Generated Time-series for Benchmarking of Causal Discovery

Time-series causal discovery (TSCD) is a fundamental problem of machine learning. However, existing synthetic datasets cannot properly evaluate or predict the algorithms' performance on real data. This study introduces the CausalTime pipeline to generate time-series that highly resemble the real data and with ground truth causal graphs for quantitative performance evaluation. The pipeline starts from real observations in a specific scenario and produces a matching benchmark dataset. Firstly, we harness deep neural networks along with normalizing flow to accurately capture realistic dynamics. Secondly, we extract hypothesized causal graphs by performing importance analysis on the neural network or leveraging prior knowledge. Thirdly, we derive the ground truth causal graphs by splitting the causal model into causal term, residual term, and noise term. Lastly, using the fitted network and the derived causal graph, we generate corresponding versatile time-series proper for algorithm assessment. In the experiments, we validate the fidelity of the generated data through qualitative and quantitative experiments, followed by a benchmarking of existing TSCD algorithms using these generated datasets. CausalTime offers a feasible solution to evaluating TSCD algorithms in real applications and can be generalized to a wide range of fields. For easy use of the proposed approach, we also provide a user-friendly website, hosted on www.causaltime.cc.

Generalized Activation via Multivariate Projection

Activation functions are essential to introduce nonlinearity into neural networks, with the Rectified Linear Unit (ReLU) often favored for its simplicity and effectiveness. Motivated by the structural similarity between a shallow Feedforward Neural Network (FNN) and a single iteration of the Projected Gradient Descent (PGD) algorithm, a standard approach for solving constrained optimization problems, we consider ReLU as a projection from R onto the nonnegative half-line R+. Building on this interpretation, we extend ReLU by substituting it with a generalized projection operator onto a convex cone, such as the Second-Order Cone (SOC) projection, thereby naturally extending it to a Multivariate Projection Unit (MPU), an activation function with multiple inputs and multiple outputs. We further provide a mathematical proof establishing that FNNs activated by SOC projections outperform those utilizing ReLU in terms of expressive power. Experimental evaluations on widely-adopted architectures further corroborate MPU's effectiveness against a broader range of existing activation functions.

HOPE: High-order Polynomial Expansion of Black-box Neural Networks

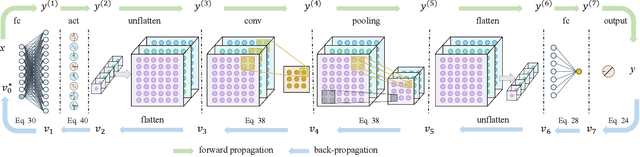
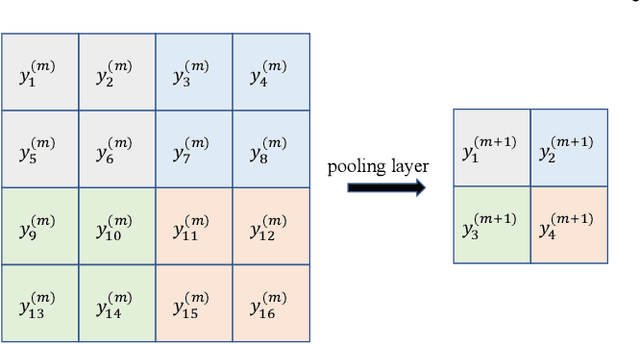
Despite their remarkable performance, deep neural networks remain mostly ``black boxes'', suggesting inexplicability and hindering their wide applications in fields requiring making rational decisions. Here we introduce HOPE (High-order Polynomial Expansion), a method for expanding a network into a high-order Taylor polynomial on a reference input. Specifically, we derive the high-order derivative rule for composite functions and extend the rule to neural networks to obtain their high-order derivatives quickly and accurately. From these derivatives, we can then derive the Taylor polynomial of the neural network, which provides an explicit expression of the network's local interpretations. Numerical analysis confirms the high accuracy, low computational complexity, and good convergence of the proposed method. Moreover, we demonstrate HOPE's wide applications built on deep learning, including function discovery, fast inference, and feature selection. The code is available at https://github.com/HarryPotterXTX/HOPE.git.

SHoP: A Deep Learning Framework for Solving High-order Partial Differential Equations

Solving partial differential equations (PDEs) has been a fundamental problem in computational science and of wide applications for both scientific and engineering research. Due to its universal approximation property, neural network is widely used to approximate the solutions of PDEs. However, existing works are incapable of solving high-order PDEs due to insufficient calculation accuracy of higher-order derivatives, and the final network is a black box without explicit explanation. To address these issues, we propose a deep learning framework to solve high-order PDEs, named SHoP. Specifically, we derive the high-order derivative rule for neural network, to get the derivatives quickly and accurately; moreover, we expand the network into a Taylor series, providing an explicit solution for the PDEs. We conduct experimental validations four high-order PDEs with different dimensions, showing that we can solve high-order PDEs efficiently and accurately.

CUTS+: High-dimensional Causal Discovery from Irregular Time-series

Causal discovery in time-series is a fundamental problem in the machine learning community, enabling causal reasoning and decision-making in complex scenarios. Recently, researchers successfully discover causality by combining neural networks with Granger causality, but their performances degrade largely when encountering high-dimensional data because of the highly redundant network design and huge causal graphs. Moreover, the missing entries in the observations further hamper the causal structural learning. To overcome these limitations, We propose CUTS+, which is built on the Granger-causality-based causal discovery method CUTS and raises the scalability by introducing a technique called Coarse-to-fine-discovery (C2FD) and leveraging a message-passing-based graph neural network (MPGNN). Compared to previous methods on simulated, quasi-real, and real datasets, we show that CUTS+ largely improves the causal discovery performance on high-dimensional data with different types of irregular sampling.

CUTS: Neural Causal Discovery from Irregular Time-Series Data

Causal discovery from time-series data has been a central task in machine learning. Recently, Granger causality inference is gaining momentum due to its good explainability and high compatibility with emerging deep neural networks. However, most existing methods assume structured input data and degenerate greatly when encountering data with randomly missing entries or non-uniform sampling frequencies, which hampers their applications in real scenarios. To address this issue, here we present CUTS, a neural Granger causal discovery algorithm to jointly impute unobserved data points and build causal graphs, via plugging in two mutually boosting modules in an iterative framework: (i) Latent data prediction stage: designs a Delayed Supervision Graph Neural Network (DSGNN) to hallucinate and register unstructured data which might be of high dimension and with complex distribution; (ii) Causal graph fitting stage: builds a causal adjacency matrix with imputed data under sparse penalty. Experiments show that CUTS effectively infers causal graphs from unstructured time-series data, with significantly superior performance to existing methods. Our approach constitutes a promising step towards applying causal discovery to real applications with non-ideal observations.

TINC: Tree-structured Implicit Neural Compression

Implicit neural representation (INR) can describe the target scenes with high fidelity using a small number of parameters, and is emerging as a promising data compression technique. However, INR in intrinsically of limited spectrum coverage, and it is non-trivial to remove redundancy in diverse complex data effectively. Preliminary studies can only exploit either global or local correlation in the target data and thus of limited performance. In this paper, we propose a Tree-structured Implicit Neural Compression (TINC) to conduct compact representation for local regions and extract the shared features of these local representations in a hierarchical manner. Specifically, we use MLPs to fit the partitioned local regions, and these MLPs are organized in tree structure to share parameters according to the spatial distance. The parameter sharing scheme not only ensures the continuity between adjacent regions, but also jointly removes the local and non-local redundancy. Extensive experiments show that TINC improves the compression fidelity of INR, and has shown impressive compression capabilities over commercial tools and other deep learning based methods. Besides, the approach is of high flexibility and can be tailored for different data and parameter settings. All the reproducible codes are going to be released on github.