DiffMOD: Progressive Diffusion Point Denoising for Moving Object Detection in Remote Sensing

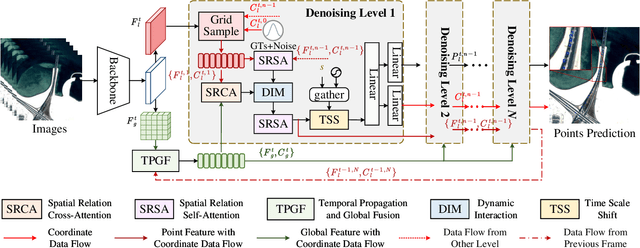
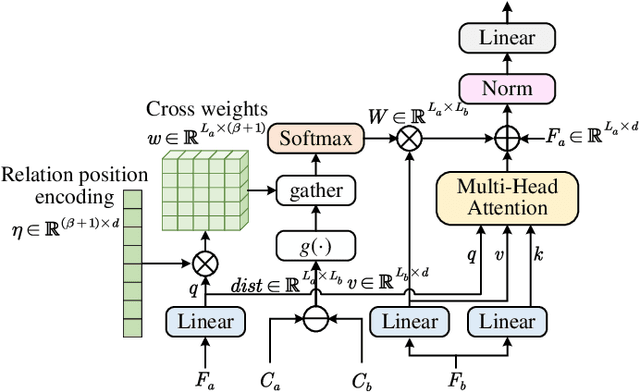
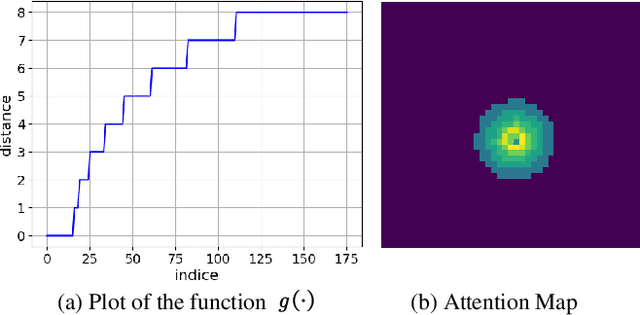
Moving object detection (MOD) in remote sensing is significantly challenged by low resolution, extremely small object sizes, and complex noise interference. Current deep learning-based MOD methods rely on probability density estimation, which restricts flexible information interaction between objects and across temporal frames. To flexibly capture high-order inter-object and temporal relationships, we propose a point-based MOD in remote sensing. Inspired by diffusion models, the network optimization is formulated as a progressive denoising process that iteratively recovers moving object centers from sparse noisy points. Specifically, we sample scattered features from the backbone outputs as atomic units for subsequent processing, while global feature embeddings are aggregated to compensate for the limited coverage of sparse point features. By modeling spatial relative positions and semantic affinities, Spatial Relation Aggregation Attention is designed to enable high-order interactions among point-level features for enhanced object representation. To enhance temporal consistency, the Temporal Propagation and Global Fusion module is designed, which leverages an implicit memory reasoning mechanism for robust cross-frame feature integration. To align with the progressive denoising process, we propose a progressive MinK optimal transport assignment strategy that establishes specialized learning objectives at each denoising level. Additionally, we introduce a missing loss function to counteract the clustering tendency of denoised points around salient objects. Experiments on the RsData remote sensing MOD dataset show that our MOD method based on scattered point denoising can more effectively explore potential relationships between sparse moving objects and improve the detection capability and temporal consistency.

Single Pass Entrywise-Transformed Low Rank Approximation

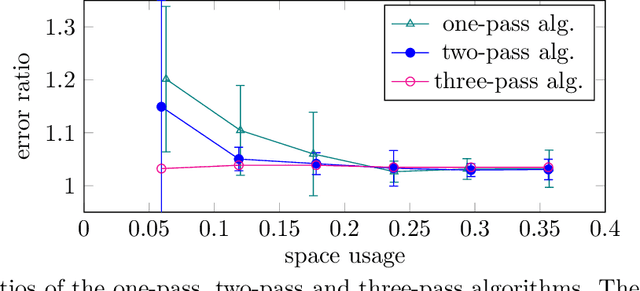
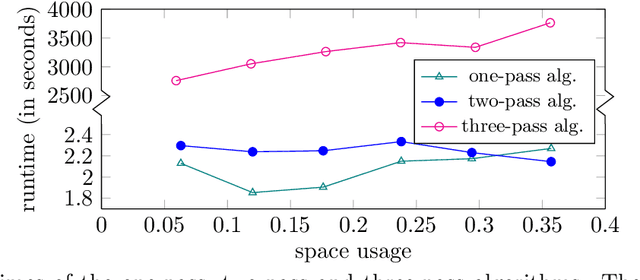
In applications such as natural language processing or computer vision, one is given a large $n \times d$ matrix $A = (a_{i,j})$ and would like to compute a matrix decomposition, e.g., a low rank approximation, of a function $f(A) = (f(a_{i,j}))$ applied entrywise to $A$. A very important special case is the likelihood function $f\left( A \right ) = \log{\left( \left| a_{ij}\right| +1\right)}$. A natural way to do this would be to simply apply $f$ to each entry of $A$, and then compute the matrix decomposition, but this requires storing all of $A$ as well as multiple passes over its entries. Recent work of Liang et al.\ shows how to find a rank-$k$ factorization to $f(A)$ for an $n \times n$ matrix $A$ using only $n \cdot \operatorname{poly}(\epsilon^{-1}k\log n)$ words of memory, with overall error $10\|f(A)-[f(A)]_k\|_F^2 + \operatorname{poly}(\epsilon/k) \|f(A)\|_{1,2}^2$, where $[f(A)]_k$ is the best rank-$k$ approximation to $f(A)$ and $\|f(A)\|_{1,2}^2$ is the square of the sum of Euclidean lengths of rows of $f(A)$. Their algorithm uses three passes over the entries of $A$. The authors pose the open question of obtaining an algorithm with $n \cdot \operatorname{poly}(\epsilon^{-1}k\log n)$ words of memory using only a single pass over the entries of $A$. In this paper we resolve this open question, obtaining the first single-pass algorithm for this problem and for the same class of functions $f$ studied by Liang et al. Moreover, our error is $\|f(A)-[f(A)]_k\|_F^2 + \operatorname{poly}(\epsilon/k) \|f(A)\|_F^2$, where $\|f(A)\|_F^2$ is the sum of squares of Euclidean lengths of rows of $f(A)$. Thus our error is significantly smaller, as it removes the factor of $10$ and also $\|f(A)\|_F^2 \leq \|f(A)\|_{1,2}^2$. We also give an algorithm for regression, pointing out an error in previous work, and empirically validate our results.

Exploring Imitation Learning for Autonomous Driving with Feedback Synthesizer and Differentiable Rasterization

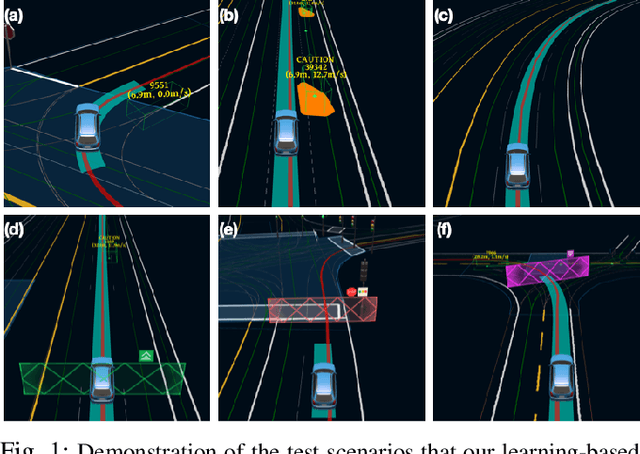
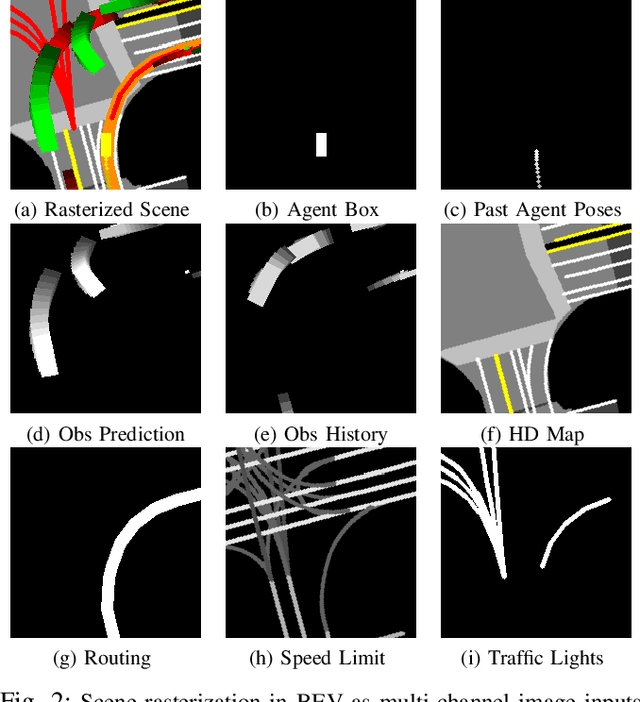
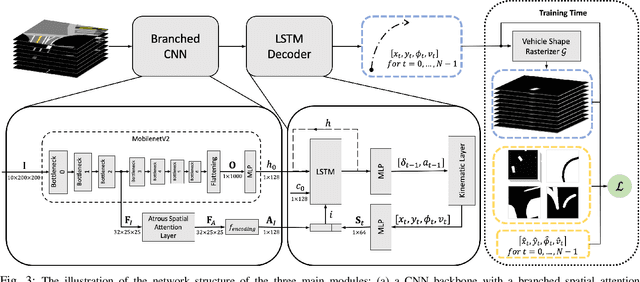
We present a learning-based planner that aims to robustly drive a vehicle by mimicking human drivers' driving behavior. We leverage a mid-to-mid approach that allows us to manipulate the input to our imitation learning network freely. With that in mind, we propose a novel feedback synthesizer for data augmentation. It allows our agent to gain more driving experience in various previously unseen environments that are likely to encounter, thus improving overall performance. This is in contrast to prior works that rely purely on random synthesizers. Furthermore, rather than completely commit to imitating, we introduce task losses that penalize undesirable behaviors, such as collision, off-road, and so on. Unlike prior works, this is done by introducing a differentiable vehicle rasterizer that directly converts the waypoints output by the network into images. This effectively avoids the usage of heavyweight ConvLSTM networks, therefore, yields a faster model inference time. About the network architecture, we exploit an attention mechanism that allows the network to reason critical objects in the scene and produce better interpretable attention heatmaps. To further enhance the safety and robustness of the network, we add an optional optimization-based post-processing planner improving the driving comfort. We comprehensively validate our method's effectiveness in different scenarios that are specifically created for evaluating self-driving vehicles. Results demonstrate that our learning-based planner achieves high intelligence and can handle complex situations. Detailed ablation and visualization analysis are included to further demonstrate each of our proposed modules' effectiveness in our method.

Lane Attention: Predicting Vehicles' Moving Trajectories by Learning Their Attention over Lanes

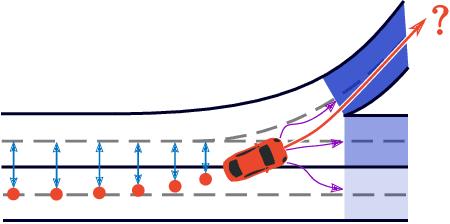
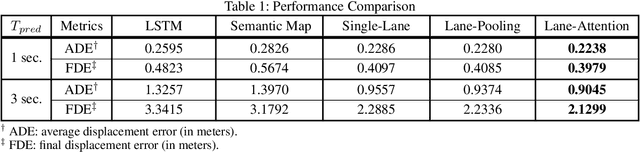
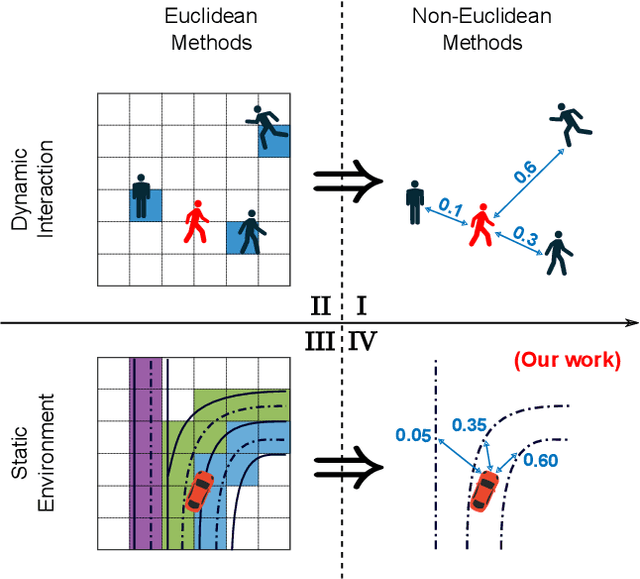
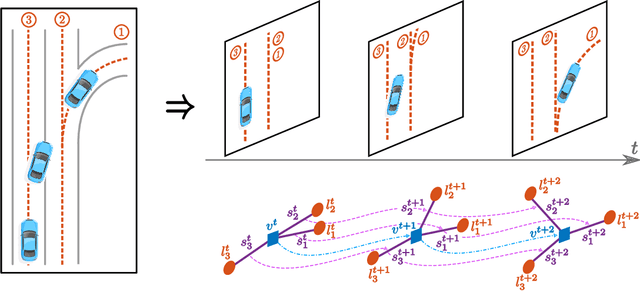
Accurately forecasting the future movements of surrounding vehicles is essential for safe and efficient operations of autonomous driving cars. This task is difficult because a vehicle's moving trajectory is greatly determined by its driver's intention, which is often hard to estimate. By leveraging attention mechanisms along with long short-term memory (LSTM) networks, this work learns the relation between a driver's intention and the vehicle's changing positions relative to road infrastructures, and uses it to guide the prediction. Different from other state-of-the-art solutions, our work treats the on-road lanes as non-Euclidean structures, unfolds the vehicle's moving history to form a spatio-temporal graph, and uses methods from Graph Neural Networks to solve the problem. Not only is our approach a pioneering attempt in using non-Euclidean methods to process static environmental features around a predicted object, our model also outperforms other state-of-the-art models in several metrics. The practicability and interpretability analysis of the model shows great potential for large-scale deployment in various autonomous driving systems in addition to our own.