Yi Fan
StealthRank: LLM Ranking Manipulation via Stealthy Prompt Optimization
Apr 08, 2025
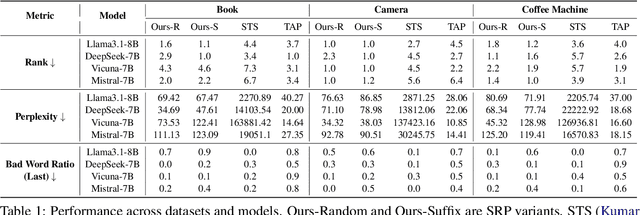


Abstract:The integration of large language models (LLMs) into information retrieval systems introduces new attack surfaces, particularly for adversarial ranking manipulations. We present StealthRank, a novel adversarial ranking attack that manipulates LLM-driven product recommendation systems while maintaining textual fluency and stealth. Unlike existing methods that often introduce detectable anomalies, StealthRank employs an energy-based optimization framework combined with Langevin dynamics to generate StealthRank Prompts (SRPs)-adversarial text sequences embedded within product descriptions that subtly yet effectively influence LLM ranking mechanisms. We evaluate StealthRank across multiple LLMs, demonstrating its ability to covertly boost the ranking of target products while avoiding explicit manipulation traces that can be easily detected. Our results show that StealthRank consistently outperforms state-of-the-art adversarial ranking baselines in both effectiveness and stealth, highlighting critical vulnerabilities in LLM-driven recommendation systems.
SCORE: Syntactic Code Representations for Static Script Malware Detection
Nov 12, 2024Abstract:As businesses increasingly adopt cloud technologies, they also need to be aware of new security challenges, such as server-side script attacks, to ensure the integrity of their systems and data. These scripts can steal data, compromise credentials, and disrupt operations. Unlike executables with standardized formats (e.g., ELF, PE), scripts are plaintext files with diverse syntax, making them harder to detect using traditional methods. As a result, more sophisticated approaches are needed to protect cloud infrastructures from these evolving threats. In this paper, we propose novel feature extraction and deep learning (DL)-based approaches for static script malware detection, targeting server-side threats. We extract features from plain-text code using two techniques: syntactic code highlighting (SCH) and abstract syntax tree (AST) construction. SCH leverages complex regexes to parse syntactic elements of code, such as keywords, variable names, etc. ASTs generate a hierarchical representation of a program's syntactic structure. We then propose a sequential and a graph-based model that exploits these feature representations to detect script malware. We evaluate our approach on more than 400K server-side scripts in Bash, Python and Perl. We use a balanced dataset of 90K scripts for training, validation, and testing, with the remaining from 400K reserved for further analysis. Experiments show that our method achieves a true positive rate (TPR) up to 81% higher than leading signature-based antivirus solutions, while maintaining a low false positive rate (FPR) of 0.17%. Moreover, our approach outperforms various neural network-based detectors, demonstrating its effectiveness in learning code maliciousness for accurate detection of script malware.
NNQS-Transformer: an Efficient and Scalable Neural Network Quantum States Approach for Ab initio Quantum Chemistry
Jul 01, 2023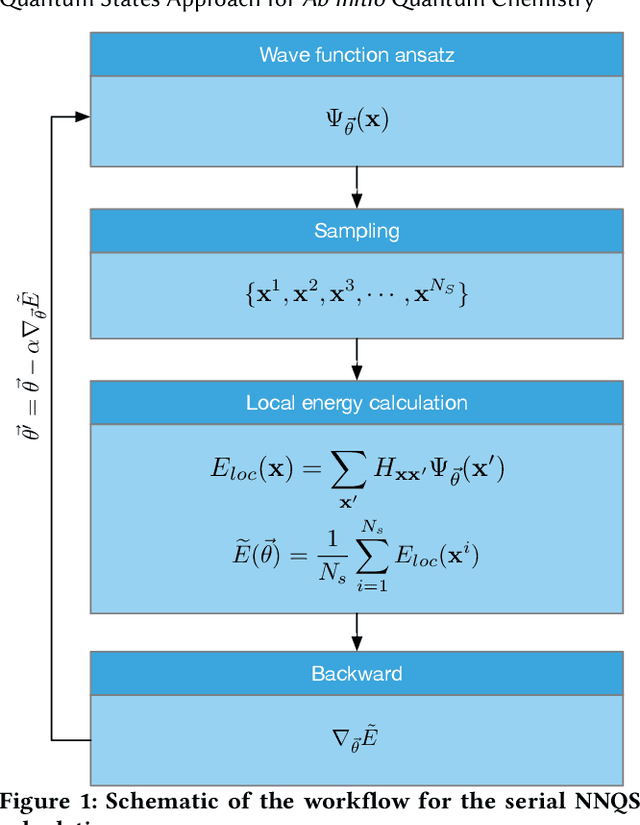
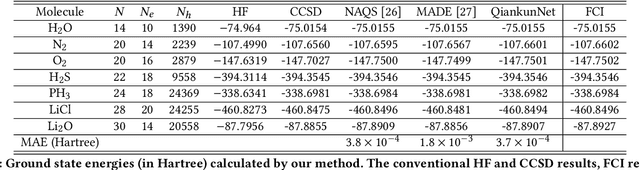
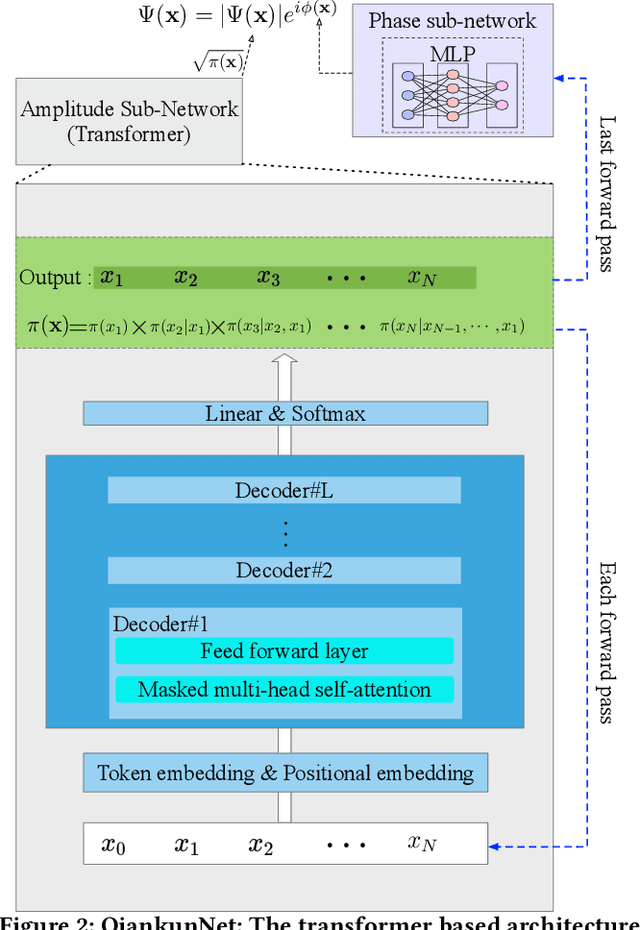
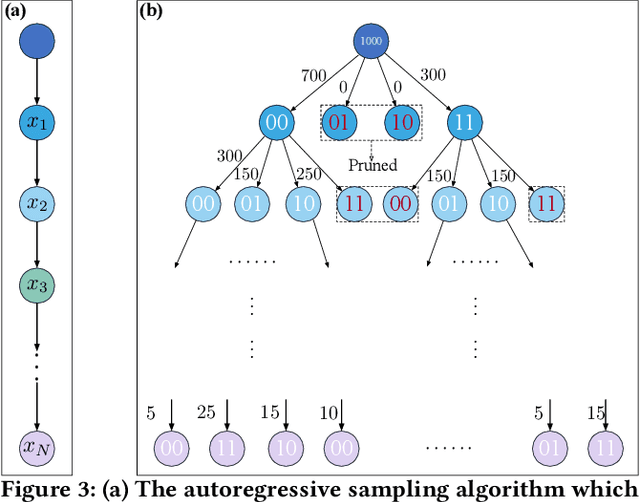
Abstract:Neural network quantum state (NNQS) has emerged as a promising candidate for quantum many-body problems, but its practical applications are often hindered by the high cost of sampling and local energy calculation. We develop a high-performance NNQS method for \textit{ab initio} electronic structure calculations. The major innovations include: (1) A transformer based architecture as the quantum wave function ansatz; (2) A data-centric parallelization scheme for the variational Monte Carlo (VMC) algorithm which preserves data locality and well adapts for different computing architectures; (3) A parallel batch sampling strategy which reduces the sampling cost and achieves good load balance; (4) A parallel local energy evaluation scheme which is both memory and computationally efficient; (5) Study of real chemical systems demonstrates both the superior accuracy of our method compared to state-of-the-art and the strong and weak scalability for large molecular systems with up to $120$ spin orbitals.
Advancing Tabu and Restart in Local Search for Maximum Weight Cliques
Apr 22, 2018
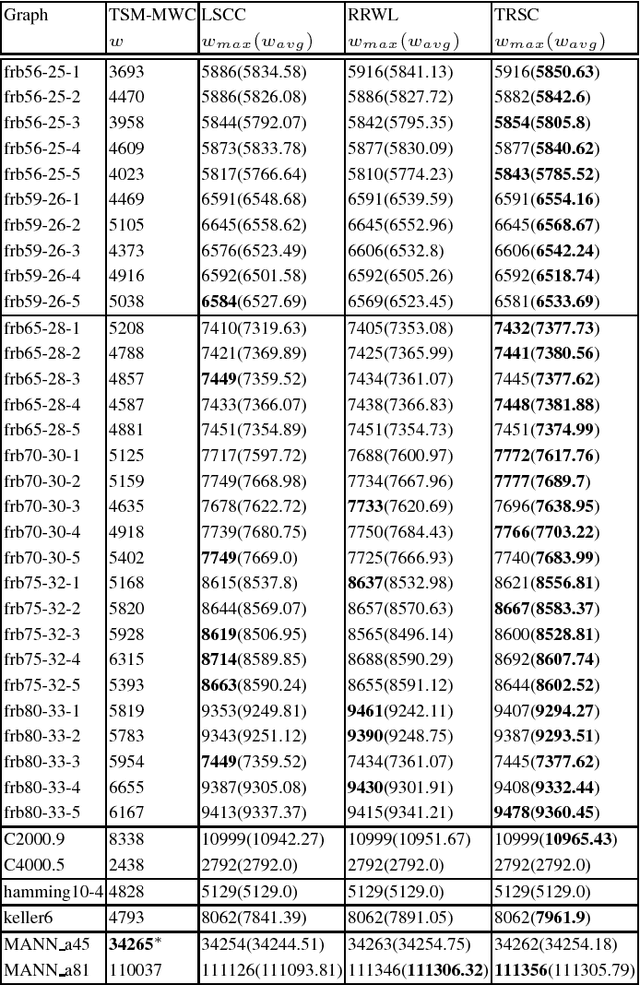
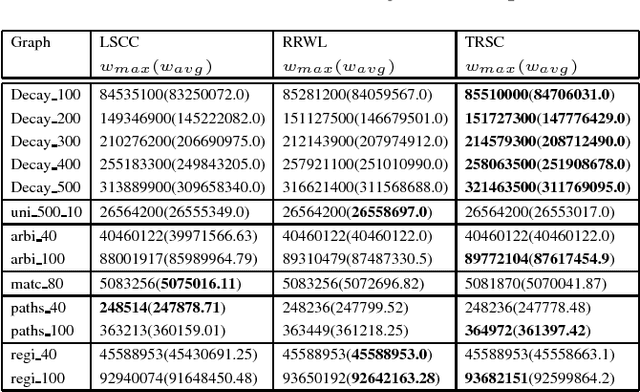
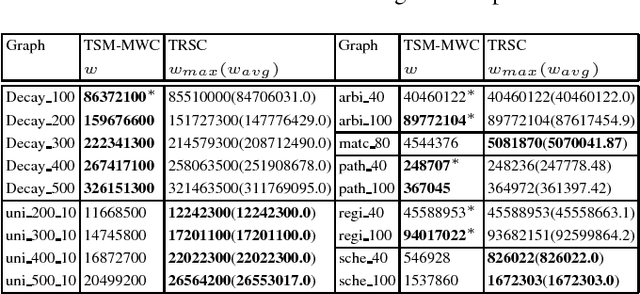
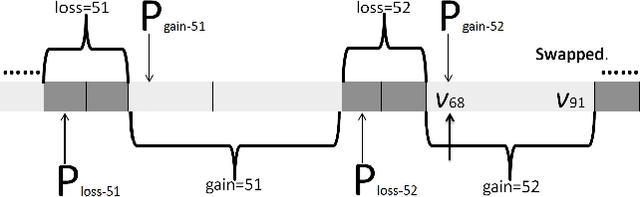
Abstract:The tabu and restart are two fundamental strategies for local search. In this paper, we improve the local search algorithms for solving the Maximum Weight Clique (MWC) problem by introducing new tabu and restart strategies. Both the tabu and restart strategies proposed are based on the notion of a local search scenario, which involves not only a candidate solution but also the tabu status and unlocking relationship. Compared to the strategy of configuration checking, our tabu mechanism discourages forming a cycle of unlocking operations. Our new restart strategy is based on the re-occurrence of a local search scenario instead of that of a candidate solution. Experimental results show that the resulting MWC solver outperforms several state-of-the-art solvers on the DIMACS, BHOSLIB, and two benchmarks from practical applications.
Exploiting Reduction Rules and Data Structures: Local Search for Minimum Vertex Cover in Massive Graphs
Sep 19, 2015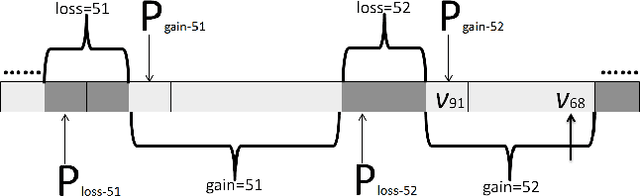
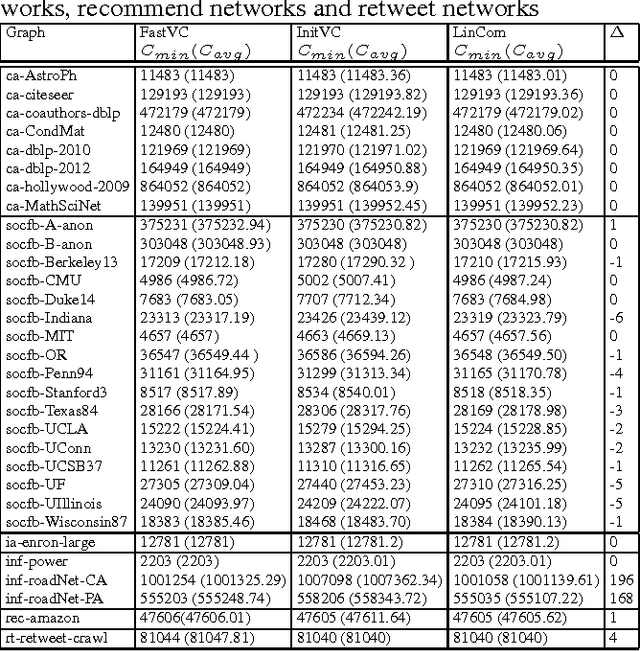
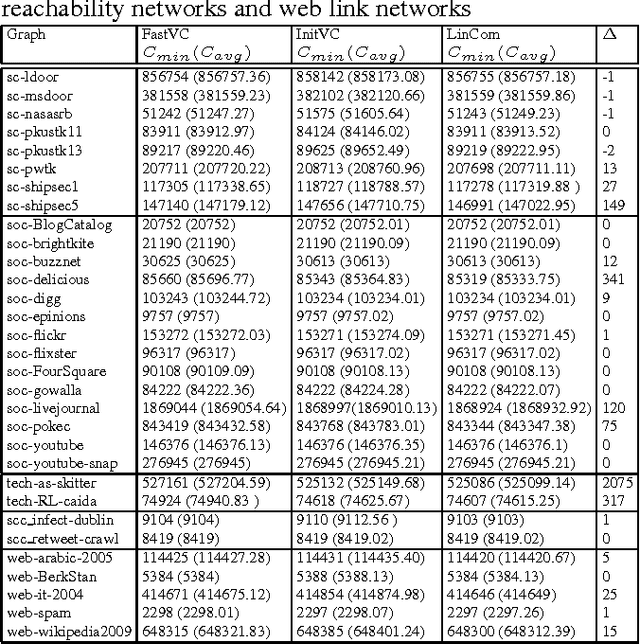
Abstract:The Minimum Vertex Cover (MinVC) problem is a well-known NP-hard problem. Recently there has been great interest in solving this problem on real-world massive graphs. For such graphs, local search is a promising approach to finding optimal or near-optimal solutions. In this paper we propose a local search algorithm that exploits reduction rules and data structures to solve the MinVC problem in such graphs. Experimental results on a wide range of real-word massive graphs show that our algorithm finds better covers than state-of-the-art local search algorithms for MinVC. Also we present interesting results about the complexities of some well-known heuristics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge