Zongjie Ma
Dropout with Tabu Strategy for Regularizing Deep Neural Networks
Aug 29, 2018

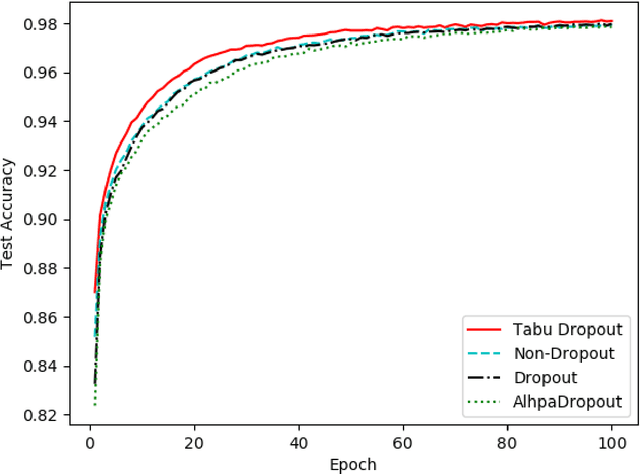
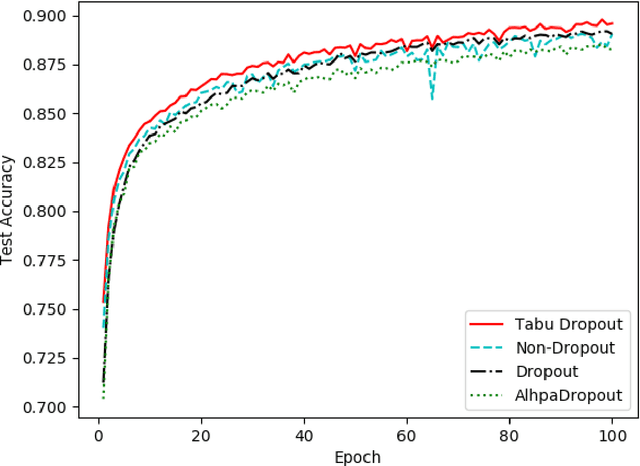
Abstract:Dropout has proven to be an effective technique for regularization and preventing the co-adaptation of neurons in deep neural networks (DNN). It randomly drops units with a probability $p$ during the training stage of DNN. Dropout also provides a way of approximately combining exponentially many different neural network architectures efficiently. In this work, we add a diversification strategy into dropout, which aims at generating more different neural network architectures in a proper times of iterations. The dropped units in last forward propagation will be marked. Then the selected units for dropping in the current FP will be kept if they have been marked in the last forward propagation. We only mark the units from the last forward propagation. We call this new technique Tabu Dropout. Tabu Dropout has no extra parameters compared with the standard Dropout and also it is computationally cheap. The experiments conducted on MNIST, Fashion-MNIST datasets show that Tabu Dropout improves the performance of the standard dropout.
Advancing Tabu and Restart in Local Search for Maximum Weight Cliques
Apr 22, 2018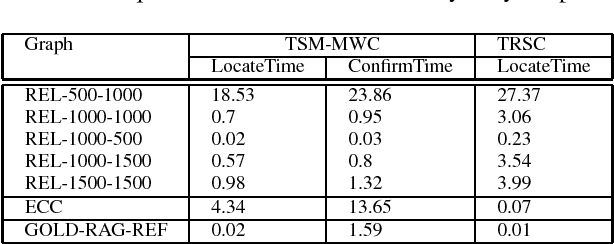
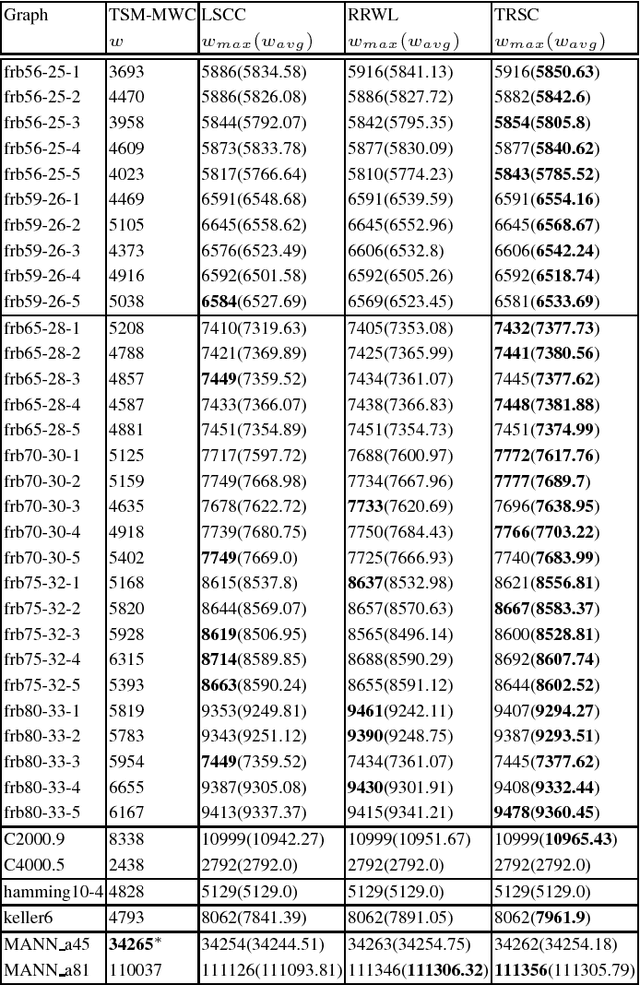
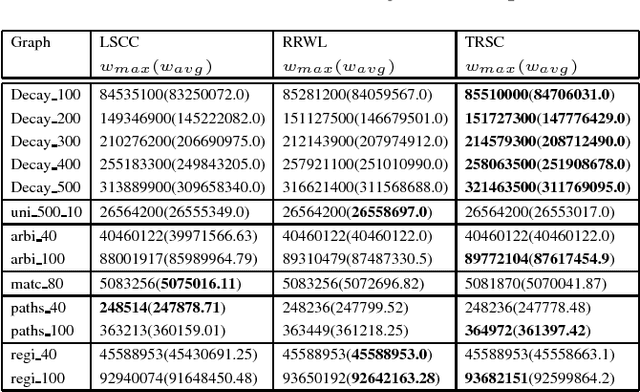
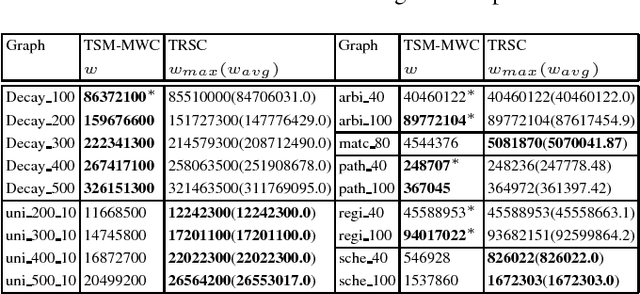
Abstract:The tabu and restart are two fundamental strategies for local search. In this paper, we improve the local search algorithms for solving the Maximum Weight Clique (MWC) problem by introducing new tabu and restart strategies. Both the tabu and restart strategies proposed are based on the notion of a local search scenario, which involves not only a candidate solution but also the tabu status and unlocking relationship. Compared to the strategy of configuration checking, our tabu mechanism discourages forming a cycle of unlocking operations. Our new restart strategy is based on the re-occurrence of a local search scenario instead of that of a candidate solution. Experimental results show that the resulting MWC solver outperforms several state-of-the-art solvers on the DIMACS, BHOSLIB, and two benchmarks from practical applications.
Exploiting Reduction Rules and Data Structures: Local Search for Minimum Vertex Cover in Massive Graphs
Sep 19, 2015
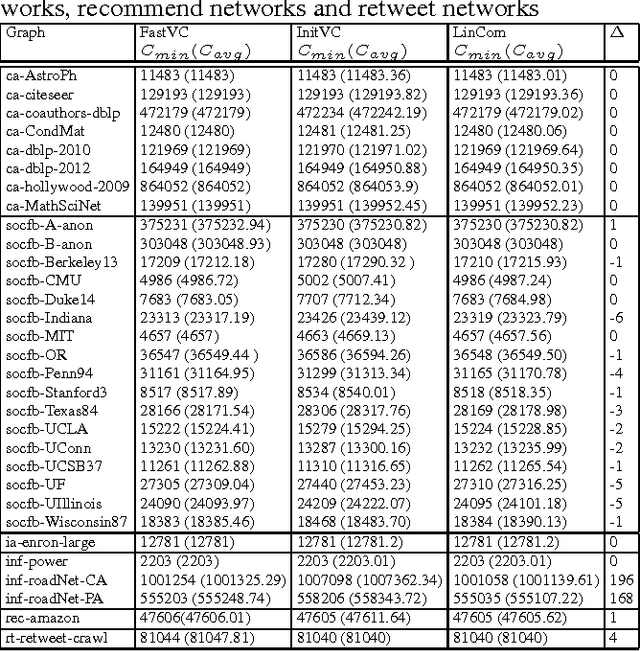
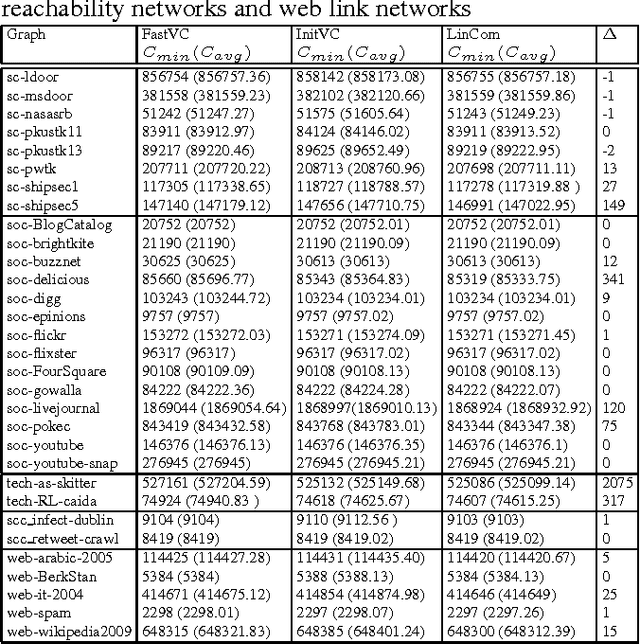
Abstract:The Minimum Vertex Cover (MinVC) problem is a well-known NP-hard problem. Recently there has been great interest in solving this problem on real-world massive graphs. For such graphs, local search is a promising approach to finding optimal or near-optimal solutions. In this paper we propose a local search algorithm that exploits reduction rules and data structures to solve the MinVC problem in such graphs. Experimental results on a wide range of real-word massive graphs show that our algorithm finds better covers than state-of-the-art local search algorithms for MinVC. Also we present interesting results about the complexities of some well-known heuristics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge