Measuring Fine-Grained Relatedness in Multitask Learning via Data Attribution

Measuring task relatedness and mitigating negative transfer remain a critical open challenge in Multitask Learning (MTL). This work extends data attribution -- which quantifies the influence of individual training data points on model predictions -- to MTL setting for measuring task relatedness. We propose the MultiTask Influence Function (MTIF), a method that adapts influence functions to MTL models with hard or soft parameter sharing. Compared to conventional task relatedness measurements, MTIF provides a fine-grained, instance-level relatedness measure beyond the entire-task level. This fine-grained relatedness measure enables a data selection strategy to effectively mitigate negative transfer in MTL. Through extensive experiments, we demonstrate that the proposed MTIF efficiently and accurately approximates the performance of models trained on data subsets. Moreover, the data selection strategy enabled by MTIF consistently improves model performance in MTL. Our work establishes a novel connection between data attribution and MTL, offering an efficient and fine-grained solution for measuring task relatedness and enhancing MTL models.

Faithful Group Shapley Value

Data Shapley is an important tool for data valuation, which quantifies the contribution of individual data points to machine learning models. In practice, group-level data valuation is desirable when data providers contribute data in batch. However, we identify that existing group-level extensions of Data Shapley are vulnerable to shell company attacks, where strategic group splitting can unfairly inflate valuations. We propose Faithful Group Shapley Value (FGSV) that uniquely defends against such attacks. Building on original mathematical insights, we develop a provably fast and accurate approximation algorithm for computing FGSV. Empirical experiments demonstrate that our algorithm significantly outperforms state-of-the-art methods in computational efficiency and approximation accuracy, while ensuring faithful group-level valuation.

GraSS: Scalable Influence Function with Sparse Gradient Compression

Gradient-based data attribution methods, such as influence functions, are critical for understanding the impact of individual training samples without requiring repeated model retraining. However, their scalability is often limited by the high computational and memory costs associated with per-sample gradient computation. In this work, we propose GraSS, a novel gradient compression algorithm and its variants FactGraSS for linear layers specifically, that explicitly leverage the inherent sparsity of per-sample gradients to achieve sub-linear space and time complexity. Extensive experiments demonstrate the effectiveness of our approach, achieving substantial speedups while preserving data influence fidelity. In particular, FactGraSS achieves up to 165% faster throughput on billion-scale models compared to the previous state-of-the-art baselines. Our code is publicly available at https://github.com/TRAIS-Lab/GraSS.

A Versatile Influence Function for Data Attribution with Non-Decomposable Loss

Influence function, a technique rooted in robust statistics, has been adapted in modern machine learning for a novel application: data attribution -- quantifying how individual training data points affect a model's predictions. However, the common derivation of influence functions in the data attribution literature is limited to loss functions that can be decomposed into a sum of individual data point losses, with the most prominent examples known as M-estimators. This restricts the application of influence functions to more complex learning objectives, which we refer to as non-decomposable losses, such as contrastive or ranking losses, where a unit loss term depends on multiple data points and cannot be decomposed further. In this work, we bridge this gap by revisiting the general formulation of influence function from robust statistics, which extends beyond M-estimators. Based on this formulation, we propose a novel method, the Versatile Influence Function (VIF), that can be straightforwardly applied to machine learning models trained with any non-decomposable loss. In comparison to the classical approach in statistics, the proposed VIF is designed to fully leverage the power of auto-differentiation, hereby eliminating the need for case-specific derivations of each loss function. We demonstrate the effectiveness of VIF across three examples: Cox regression for survival analysis, node embedding for network analysis, and listwise learning-to-rank for information retrieval. In all cases, the influence estimated by VIF closely resembles the results obtained by brute-force leave-one-out retraining, while being up to $10^3$ times faster to compute. We believe VIF represents a significant advancement in data attribution, enabling efficient influence-function-based attribution across a wide range of machine learning paradigms, with broad potential for practical use cases.

Optimizing Cox Models with Stochastic Gradient Descent: Theoretical Foundations and Practical Guidances

Optimizing Cox regression and its neural network variants poses substantial computational challenges in large-scale studies. Stochastic gradient descent (SGD), known for its scalability in model optimization, has recently been adapted to optimize Cox models. Unlike its conventional application, which typically targets a sum of independent individual loss, SGD for Cox models updates parameters based on the partial likelihood of a subset of data. Despite its empirical success, the theoretical foundation for optimizing Cox partial likelihood with SGD is largely underexplored. In this work, we demonstrate that the SGD estimator targets an objective function that is batch-size-dependent. We establish that the SGD estimator for the Cox neural network (Cox-NN) is consistent and achieves the optimal minimax convergence rate up to a polylogarithmic factor. For Cox regression, we further prove the $\sqrt{n}$-consistency and asymptotic normality of the SGD estimator, with variance depending on the batch size. Furthermore, we quantify the impact of batch size on Cox-NN training and its effect on the SGD estimator's asymptotic efficiency in Cox regression. These findings are validated by extensive numerical experiments and provide guidance for selecting batch sizes in SGD applications. Finally, we demonstrate the effectiveness of SGD in a real-world application where GD is unfeasible due to the large scale of data.

Minimax Regret Learning for Data with Heterogeneous Subgroups

Modern complex datasets often consist of various sub-populations. To develop robust and generalizable methods in the presence of sub-population heterogeneity, it is important to guarantee a uniform learning performance instead of an average one. In many applications, prior information is often available on which sub-population or group the data points belong to. Given the observed groups of data, we develop a min-max-regret (MMR) learning framework for general supervised learning, which targets to minimize the worst-group regret. Motivated from the regret-based decision theoretic framework, the proposed MMR is distinguished from the value-based or risk-based robust learning methods in the existing literature. The regret criterion features several robustness and invariance properties simultaneously. In terms of generalizability, we develop the theoretical guarantee for the worst-case regret over a super-population of the meta data, which incorporates the observed sub-populations, their mixtures, as well as other unseen sub-populations that could be approximated by the observed ones. We demonstrate the effectiveness of our method through extensive simulation studies and an application to kidney transplantation data from hundreds of transplant centers.

KL-divergence Based Deep Learning for Discrete Time Model

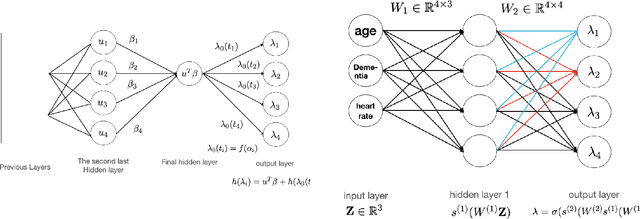
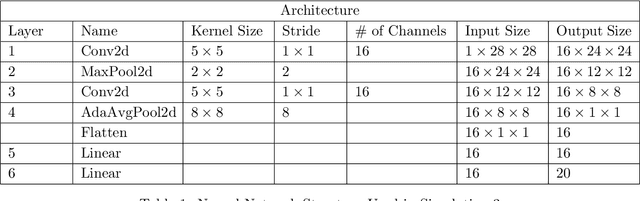
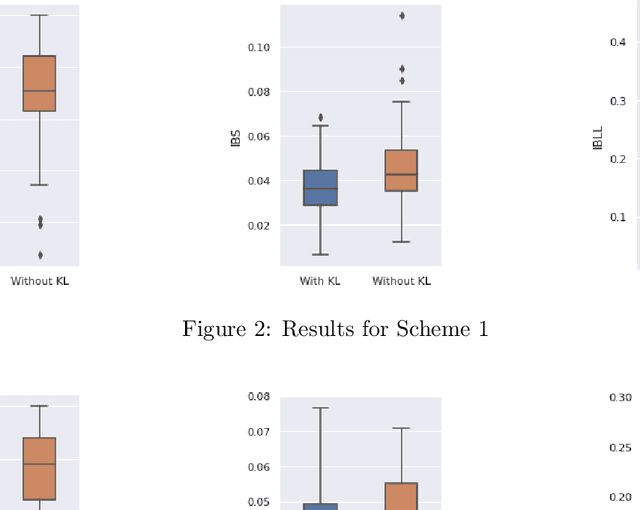
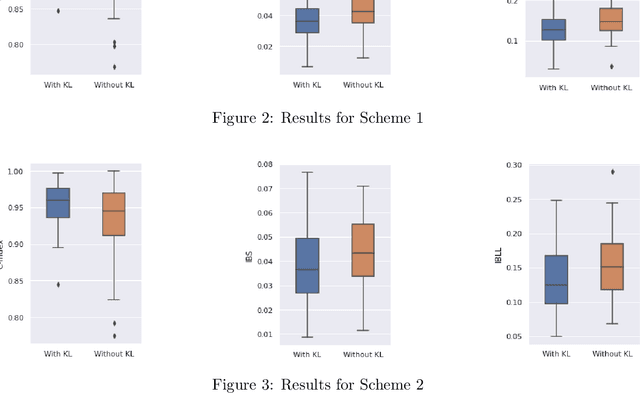
Neural Network (Deep Learning) is a modern model in Artificial Intelligence and it has been exploited in Survival Analysis. Although several improvements have been shown by previous works, training an excellent deep learning model requires a huge amount of data, which may not hold in practice. To address this challenge, we develop a Kullback-Leibler-based (KL) deep learning procedure to integrate external survival prediction models with newly collected time-to-event data. Time-dependent KL discrimination information is utilized to measure the discrepancy between the external and internal data. This is the first work considering using prior information to deal with short data problem in Survival Analysis for deep learning. Simulation and real data results show that the proposed model achieves better performance and higher robustness compared with previous works.

SODEN: A Scalable Continuous-Time Survival Model through Ordinary Differential Equation Networks

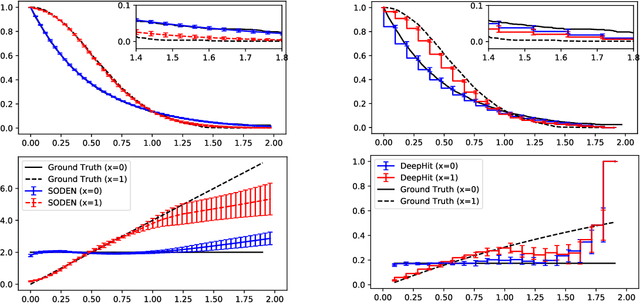
In this paper, we propose a flexible model for survival analysis using neural networks along with scalable optimization algorithms. One key technical challenge for directly applying maximum likelihood estimation (MLE) to censored data is that evaluating the objective function and its gradients with respect to model parameters requires the calculation of integrals. To address this challenge, we recognize that the MLE for censored data can be viewed as a differential-equation constrained optimization problem, a novel perspective. Following this connection, we model the distribution of event time through an ordinary differential equation and utilize efficient ODE solvers and adjoint sensitivity analysis to numerically evaluate the likelihood and the gradients. Using this approach, we are able to 1) provide a broad family of continuous-time survival distributions without strong structural assumptions, 2) obtain powerful feature representations using neural networks, and 3) allow efficient estimation of the model in large-scale applications using stochastic gradient descent. Through both simulation studies and real-world data examples, we demonstrate the effectiveness of the proposed method in comparison to existing state-of-the-art deep learning survival analysis models.

Learning-to-Rank with Partitioned Preference: Fast Estimation for the Plackett-Luce Model

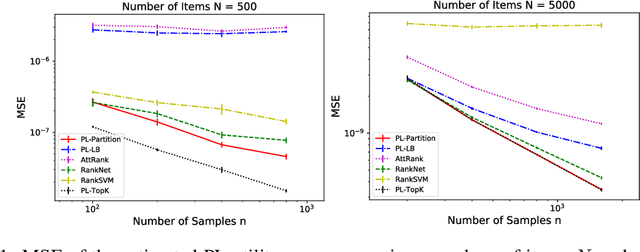
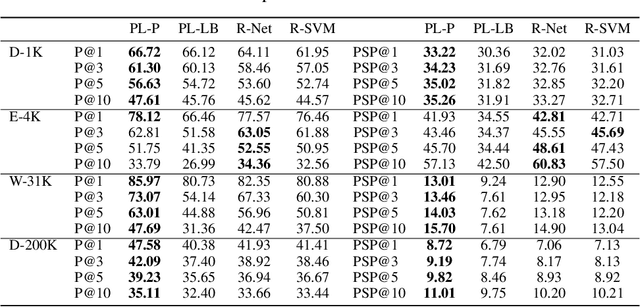
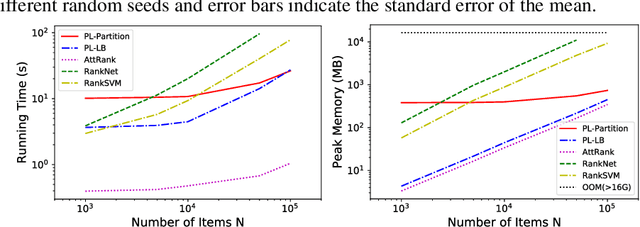
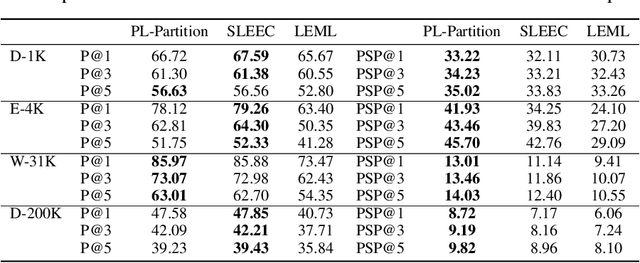
We consider the problem of listwise learning-to-rank (LTR) on data with \textit{partitioned preference}, where a set of items are sliced into ordered and disjoint partitions, but the ranking of items within a partition is unknown. The Plackett-Luce (PL) model has been widely used in listwise LTR methods. However, given $N$ items with $M$ partitions, calculating the likelihood of data with partitioned preference under the PL model has a time complexity of $O(N+S!)$, where $S$ is the maximum size of the top $M-1$ partitions. This computational challenge restrains existing PL-based listwise LTR methods to only a special case of partitioned preference, \textit{top-$K$ ranking}, where the exact order of the top $K$ items is known. In this paper, we exploit a random utility model formulation of the PL model and propose an efficient approach through numerical integration for calculating the likelihood. This numerical approach reduces the aforementioned time complexity to $O(N+MS)$, which allows training deep-neural-network-based ranking models with a large output space. We demonstrate that the proposed method outperforms well-known LTR baselines and remains scalable through both simulation experiments and applications to real-world eXtreme Multi-Label (XML) classification tasks. The proposed method also achieves state-of-the-art performance on XML datasets with relatively large numbers of labels per sample.

A Flexible Generative Framework for Graph-based Semi-supervised Learning

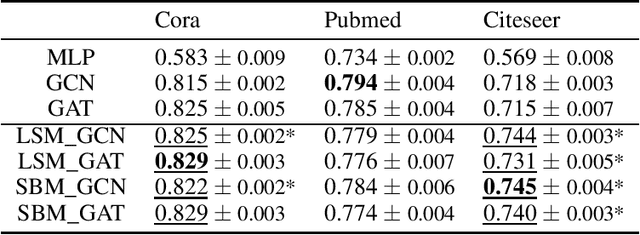
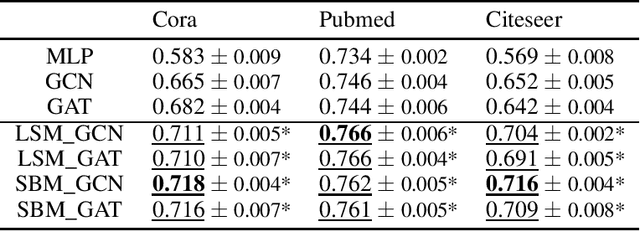
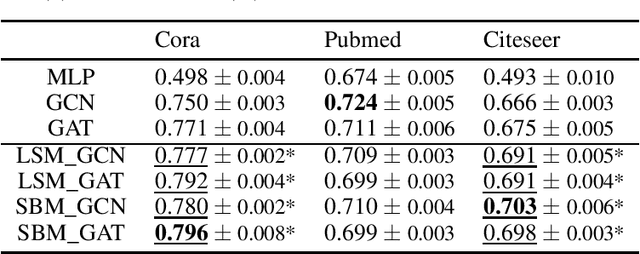
We consider a family of problems that are concerned about making predictions for the majority of unlabeled, graph-structured data samples based on a small proportion of labeled examples. Relational information among the data samples, often encoded in the graph or network structure, is shown to be helpful for these semi-supervised learning tasks. Conventional graph-based regularization methods and recent graph neural networks do not fully leverage the interrelations between the features, the graph, and the labels. We propose a flexible generative framework for graph-based semi-supervised learning, which approaches the joint distribution of the node features, labels, and the graph structure. Borrowing insights from random graph models in network science literature, this joint distribution can be instantiated using various distribution families. For the inference of missing labels, we exploit recent advances of scalable variational inference techniques to approximate the Bayesian posterior. We conduct thorough experiments on benchmark datasets for graph-based semi-supervised learning. Results show that the proposed methods outperform state-of-the-art models under most settings.