Kolmogorov GAM Networks are all you need!

Kolmogorov GAM (K-GAM) networks are shown to be an efficient architecture for training and inference. They are an additive model with an embedding that is independent of the function of interest. They provide an alternative to the transformer architecture. They are the machine learning version of Kolmogorov's Superposition Theorem (KST) which provides an efficient representations of a multivariate function. Such representations have use in machine learning for encoding dictionaries (a.k.a. "look-up" tables). KST theory also provides a representation based on translates of the K\"oppen function. The goal of our paper is to interpret this representation in a machine learning context for applications in Artificial Intelligence (AI). Our architecture is equivalent to a topological embedding which is independent of the function together with an additive layer that uses a Generalized Additive Model (GAM). This provides a class of learning procedures with far fewer parameters than current deep learning algorithms. Implementation can be parallelizable which makes our algorithms computationally attractive. To illustrate our methodology, we use the Iris data from statistical learning. We also show that our additive model with non-linear embedding provides an alternative to transformer architectures which from a statistical viewpoint are kernel smoothers. Additive KAN models therefore provide a natural alternative to transformers. Finally, we conclude with directions for future research.

Generative Bayesian Computation for Maximum Expected Utility

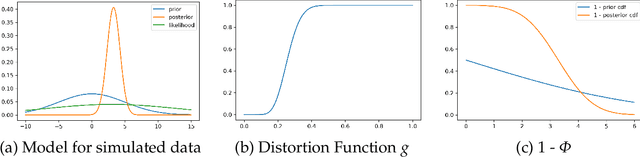
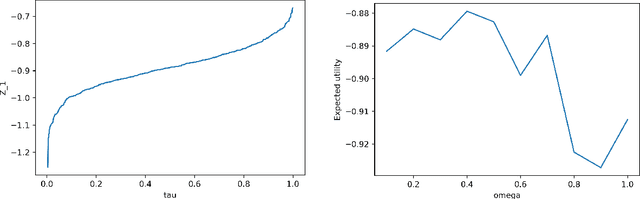
Generative Bayesian Computation (GBC) methods are developed to provide an efficient computational solution for maximum expected utility (MEU). We propose a density-free generative method based on quantiles that naturally calculates expected utility as a marginal of quantiles. Our approach uses a deep quantile neural estimator to directly estimate distributional utilities. Generative methods assume only the ability to simulate from the model and parameters and as such are likelihood-free. A large training dataset is generated from parameters and output together with a base distribution. Our method a number of computational advantages primarily being density-free with an efficient estimator of expected utility. A link with the dual theory of expected utility and risk taking is also discussed. To illustrate our methodology, we solve an optimal portfolio allocation problem with Bayesian learning and a power utility (a.k.a. fractional Kelly criterion). Finally, we conclude with directions for future research.

Deep Learning: A Tutorial

Our goal is to provide a review of deep learning methods which provide insight into structured high-dimensional data. Rather than using shallow additive architectures common to most statistical models, deep learning uses layers of semi-affine input transformations to provide a predictive rule. Applying these layers of transformations leads to a set of attributes (or, features) to which probabilistic statistical methods can be applied. Thus, the best of both worlds can be achieved: scalable prediction rules fortified with uncertainty quantification, where sparse regularization finds the features.

The Value of Chess Squares

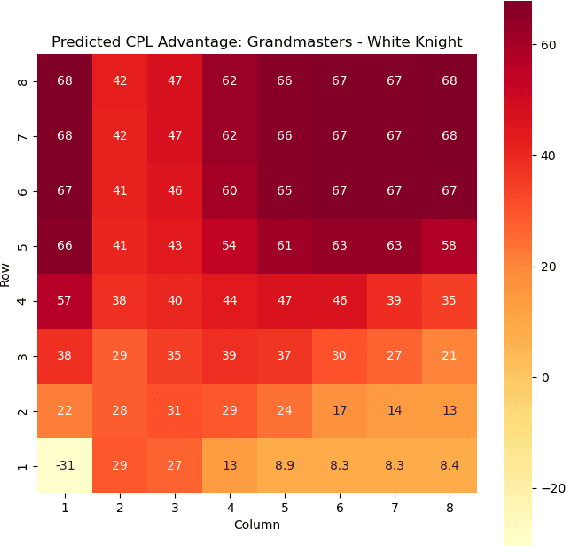
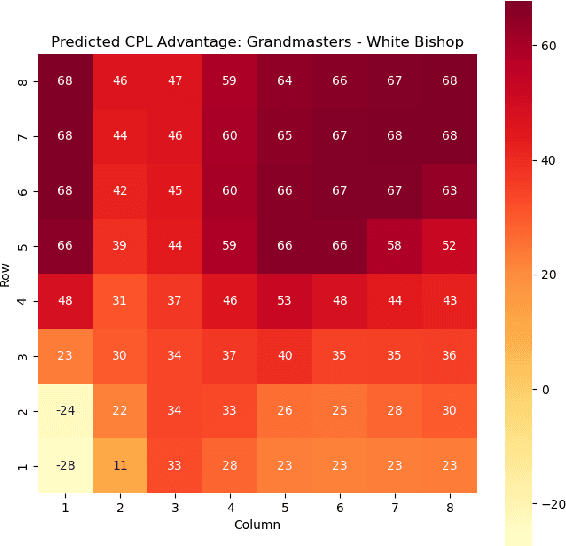
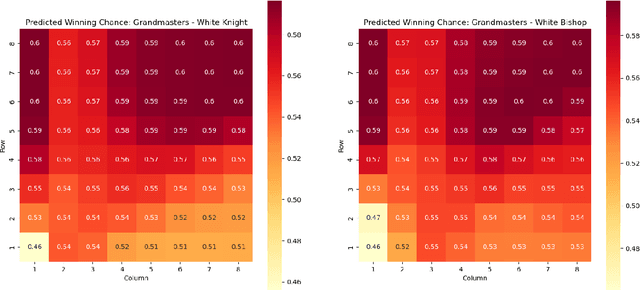
Valuing chess squares and determining the placement of pieces on the board are the main objectives of our study. With the emergence of chess AI, it has become possible to accurately assess the worth of positions in a game of chess. The conventional approach assigns fixed values to pieces $(\symking=\infty, \symqueen=9, \symrook=5, \symbishop=3, \symknight=3, \sympawn=1)$. We enhance this analysis by introducing marginal valuations for both pieces and squares. We demonstrate our method by examining the positioning of Knights and Bishops, and also provide valuable insights into the valuation of pawns. Notably, Nimzowitsch was among the pioneers in advocating for the significance of Pawn structure and valuation. Finally, we conclude by suggesting potential avenues for future research.

Quantum Bayes AI

Quantum Bayesian AI (Q-B) is an emerging field that levers the computational gains available in Quantum computing. The promise is an exponential speed-up in many Bayesian algorithms. Our goal is to apply these methods directly to statistical and machine learning problems. We provide a duality between classical and quantum probability for calculating of posterior quantities of interest. Our framework unifies MCMC, Deep Learning and Quantum Learning calculations from the viewpoint from von Neumann's principle of quantum measurement. Quantum embeddings and neural gates are also an important part of data encoding and feature selection. There is a natural duality with well-known kernel methods in statistical learning. We illustrate the behaviour of quantum algorithms on two simple classification algorithms. Finally, we conclude with directions for future research.

Bayesian Calibration for Activity Based Models

We consider the problem of calibration and uncertainty analysis for activity-based transportation simulators. ABMs rely on statistical models of traveler's behavior to predict travel patterns in a metropolitan area. Input parameters are typically estimated from traveler's surveys using maximum likelihood. We develop an approach that uses Gaussian process emulator to calibrate an activity-based model of a metropolitan transplantation system. Our approach extends traditional emulators to handle high-dimensional and non-stationary nature of the transportation simulator. Our methodology is applied to transportation simulator of Bloomington, Illinois. We calibrate key parameters of the model and compare to the ad-hoc calibration process.

Deep Generative Models for Vehicle Speed Trajectories

Generating realistic vehicle speed trajectories is a crucial component in evaluating vehicle fuel economy and in predictive control of self-driving cars. Traditional generative models rely on Markov chain methods and can produce accurate synthetic trajectories but are subject to the curse of dimensionality. They do not allow to include conditional input variables into the generation process. In this paper, we show how extensions to deep generative models allow accurate and scalable generation. Proposed architectures involve recurrent and feed-forward layers and are trained using adversarial techniques. Our models are shown to perform well on generating vehicle trajectories using a model trained on GPS data from Chicago metropolitan area.

Merging Two Cultures: Deep and Statistical Learning

Merging the two cultures of deep and statistical learning provides insights into structured high-dimensional data. Traditional statistical modeling is still a dominant strategy for structured tabular data. Deep learning can be viewed through the lens of generalized linear models (GLMs) with composite link functions. Sufficient dimensionality reduction (SDR) and sparsity performs nonlinear feature engineering. We show that prediction, interpolation and uncertainty quantification can be achieved using probabilistic methods at the output layer of the model. Thus a general framework for machine learning arises that first generates nonlinear features (a.k.a factors) via sparse regularization and stochastic gradient optimisation and second uses a stochastic output layer for predictive uncertainty. Rather than using shallow additive architectures as in many statistical models, deep learning uses layers of semi affine input transformations to provide a predictive rule. Applying these layers of transformations leads to a set of attributes (a.k.a features) to which predictive statistical methods can be applied. Thus we achieve the best of both worlds: scalability and fast predictive rule construction together with uncertainty quantification. Sparse regularisation with un-supervised or supervised learning finds the features. We clarify the duality between shallow and wide models such as PCA, PPR, RRR and deep but skinny architectures such as autoencoders, MLPs, CNN, and LSTM. The connection with data transformations is of practical importance for finding good network architectures. By incorporating probabilistic components at the output level we allow for predictive uncertainty. For interpolation we use deep Gaussian process and ReLU trees for classification. We provide applications to regression, classification and interpolation. Finally, we conclude with directions for future research.

Solving Large-Scale 0-1 Knapsack Problems and its Application to Point Cloud Resampling

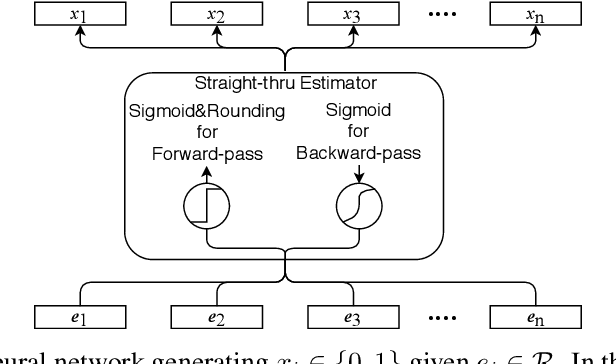
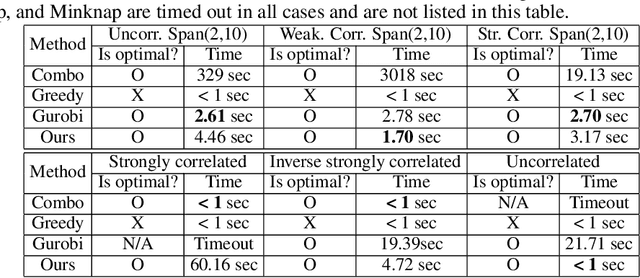
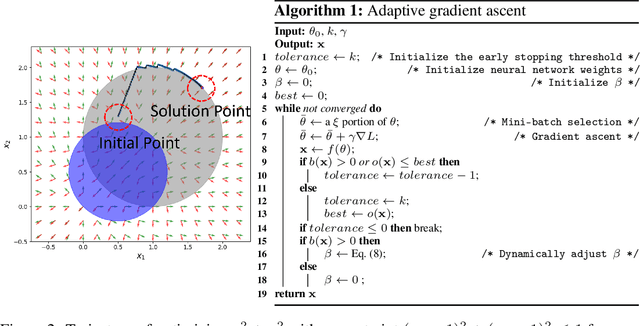
0-1 knapsack is of fundamental importance in computer science, business, operations research, etc. In this paper, we present a deep learning technique-based method to solve large-scale 0-1 knapsack problems where the number of products (items) is large and/or the values of products are not necessarily predetermined but decided by an external value assignment function during the optimization process. Our solution is greatly inspired by the method of Lagrange multiplier and some recent adoptions of game theory to deep learning. After formally defining our proposed method based on them, we develop an adaptive gradient ascent method to stabilize its optimization process. In our experiments, the presented method solves all the large-scale benchmark KP instances in a minute whereas existing methods show fluctuating runtime. We also show that our method can be used for other applications, including but not limited to the point cloud resampling.

Deep Learning: Computational Aspects

In this article we review computational aspects of Deep Learning (DL). Deep learning uses network architectures consisting of hierarchical layers of latent variables to construct predictors for high-dimensional input-output models. Training a deep learning architecture is computationally intensive, and efficient linear algebra libraries is the key for training and inference. Stochastic gradient descent (SGD) optimization and batch sampling are used to learn from massive data sets.