Bayesian Deep ICE

Deep Independent Component Estimation (DICE) has many applications in modern day machine learning as a feature engineering extraction method. We provide a novel latent variable representation of independent component analysis that enables both point estimates via expectation-maximization (EM) and full posterior sampling via Markov Chain Monte Carlo (MCMC) algorithms. Our methodology also applies to flow-based methods for nonlinear feature extraction. We discuss how to implement conditional posteriors and envelope-based methods for optimization. Through this representation hierarchy, we unify a number of hitherto disjoint estimation procedures. We illustrate our methodology and algorithms on a numerical example. Finally, we conclude with directions for future research.

Merging Two Cultures: Deep and Statistical Learning

Merging the two cultures of deep and statistical learning provides insights into structured high-dimensional data. Traditional statistical modeling is still a dominant strategy for structured tabular data. Deep learning can be viewed through the lens of generalized linear models (GLMs) with composite link functions. Sufficient dimensionality reduction (SDR) and sparsity performs nonlinear feature engineering. We show that prediction, interpolation and uncertainty quantification can be achieved using probabilistic methods at the output layer of the model. Thus a general framework for machine learning arises that first generates nonlinear features (a.k.a factors) via sparse regularization and stochastic gradient optimisation and second uses a stochastic output layer for predictive uncertainty. Rather than using shallow additive architectures as in many statistical models, deep learning uses layers of semi affine input transformations to provide a predictive rule. Applying these layers of transformations leads to a set of attributes (a.k.a features) to which predictive statistical methods can be applied. Thus we achieve the best of both worlds: scalability and fast predictive rule construction together with uncertainty quantification. Sparse regularisation with un-supervised or supervised learning finds the features. We clarify the duality between shallow and wide models such as PCA, PPR, RRR and deep but skinny architectures such as autoencoders, MLPs, CNN, and LSTM. The connection with data transformations is of practical importance for finding good network architectures. By incorporating probabilistic components at the output level we allow for predictive uncertainty. For interpolation we use deep Gaussian process and ReLU trees for classification. We provide applications to regression, classification and interpolation. Finally, we conclude with directions for future research.

FairMixRep : Self-supervised Robust Representation Learning for Heterogeneous Data with Fairness constraints

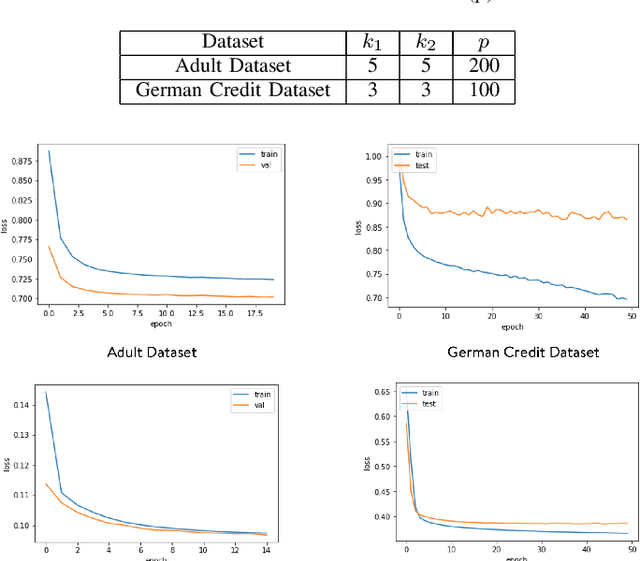
Representation Learning in a heterogeneous space with mixed variables of numerical and categorical types has interesting challenges due to its complex feature manifold. Moreover, feature learning in an unsupervised setup, without class labels and a suitable learning loss function, adds to the problem complexity. Further, the learned representation and subsequent predictions should not reflect discriminatory behavior towards certain sensitive groups or attributes. The proposed feature map should preserve maximum variations present in the data and needs to be fair with respect to the sensitive variables. We propose, in the first phase of our work, an efficient encoder-decoder framework to capture the mixed-domain information. The second phase of our work focuses on de-biasing the mixed space representations by adding relevant fairness constraints. This ensures minimal information loss between the representations before and after the fairness-preserving projections. Both the information content and the fairness aspect of the final representation learned has been validated through several metrics where it shows excellent performance. Our work (FairMixRep) addresses the problem of Mixed Space Fair Representation learning from an unsupervised perspective and learns a Universal representation that is timely, unique, and a novel research contribution.

Horseshoe Regularization for Machine Learning in Complex and Deep Models

Since the advent of the horseshoe priors for regularization, global-local shrinkage methods have proved to be a fertile ground for the development of Bayesian methodology in machine learning, specifically for high-dimensional regression and classification problems. They have achieved remarkable success in computation, and enjoy strong theoretical support. Most of the existing literature has focused on the linear Gaussian case; see Bhadra et al. (2019) for a systematic survey. The purpose of the current article is to demonstrate that the horseshoe regularization is useful far more broadly, by reviewing both methodological and computational developments in complex models that are more relevant to machine learning applications. Specifically, we focus on methodological challenges in horseshoe regularization in nonlinear and non-Gaussian models; multivariate models; and deep neural networks. We also outline the recent computational developments in horseshoe shrinkage for complex models along with a list of available software implementations that allows one to venture out beyond the comfort zone of the canonical linear regression problems.

Horseshoe Regularization for Feature Subset Selection

Feature subset selection arises in many high-dimensional applications of statistics, such as compressed sensing and genomics. The $\ell_0$ penalty is ideal for this task, the caveat being it requires the NP-hard combinatorial evaluation of all models. A recent area of considerable interest is to develop efficient algorithms to fit models with a non-convex $\ell_\gamma$ penalty for $\gamma\in (0,1)$, which results in sparser models than the convex $\ell_1$ or lasso penalty, but is harder to fit. We propose an alternative, termed the horseshoe regularization penalty for feature subset selection, and demonstrate its theoretical and computational advantages. The distinguishing feature from existing non-convex optimization approaches is a full probabilistic representation of the penalty as the negative of the logarithm of a suitable prior, which in turn enables efficient expectation-maximization and local linear approximation algorithms for optimization and MCMC for uncertainty quantification. In synthetic and real data, the resulting algorithms provide better statistical performance, and the computation requires a fraction of time of state-of-the-art non-convex solvers.