Quantum Bayes AI

Quantum Bayesian AI (Q-B) is an emerging field that levers the computational gains available in Quantum computing. The promise is an exponential speed-up in many Bayesian algorithms. Our goal is to apply these methods directly to statistical and machine learning problems. We provide a duality between classical and quantum probability for calculating of posterior quantities of interest. Our framework unifies MCMC, Deep Learning and Quantum Learning calculations from the viewpoint from von Neumann's principle of quantum measurement. Quantum embeddings and neural gates are also an important part of data encoding and feature selection. There is a natural duality with well-known kernel methods in statistical learning. We illustrate the behaviour of quantum algorithms on two simple classification algorithms. Finally, we conclude with directions for future research.

Merging Two Cultures: Deep and Statistical Learning

Merging the two cultures of deep and statistical learning provides insights into structured high-dimensional data. Traditional statistical modeling is still a dominant strategy for structured tabular data. Deep learning can be viewed through the lens of generalized linear models (GLMs) with composite link functions. Sufficient dimensionality reduction (SDR) and sparsity performs nonlinear feature engineering. We show that prediction, interpolation and uncertainty quantification can be achieved using probabilistic methods at the output layer of the model. Thus a general framework for machine learning arises that first generates nonlinear features (a.k.a factors) via sparse regularization and stochastic gradient optimisation and second uses a stochastic output layer for predictive uncertainty. Rather than using shallow additive architectures as in many statistical models, deep learning uses layers of semi affine input transformations to provide a predictive rule. Applying these layers of transformations leads to a set of attributes (a.k.a features) to which predictive statistical methods can be applied. Thus we achieve the best of both worlds: scalability and fast predictive rule construction together with uncertainty quantification. Sparse regularisation with un-supervised or supervised learning finds the features. We clarify the duality between shallow and wide models such as PCA, PPR, RRR and deep but skinny architectures such as autoencoders, MLPs, CNN, and LSTM. The connection with data transformations is of practical importance for finding good network architectures. By incorporating probabilistic components at the output level we allow for predictive uncertainty. For interpolation we use deep Gaussian process and ReLU trees for classification. We provide applications to regression, classification and interpolation. Finally, we conclude with directions for future research.

Bayesian Inference for Gamma Models

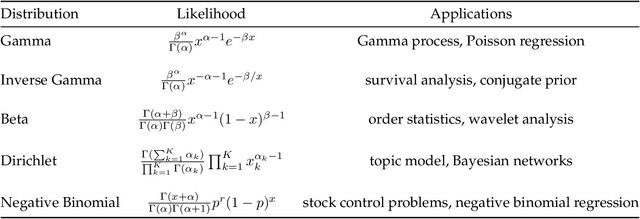
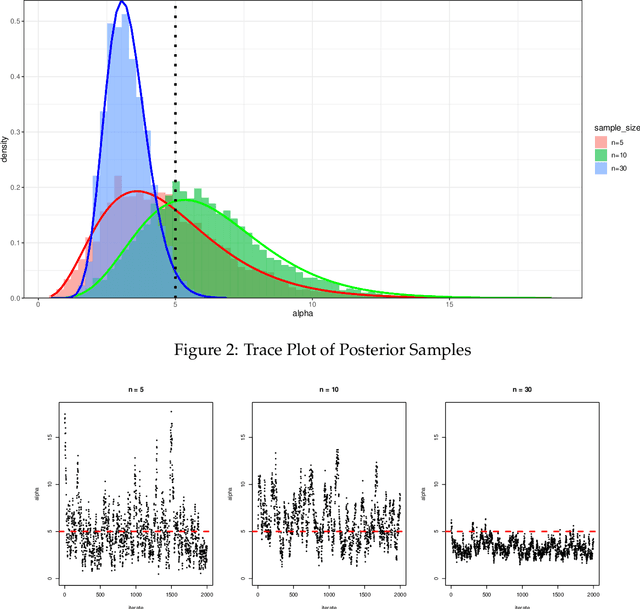
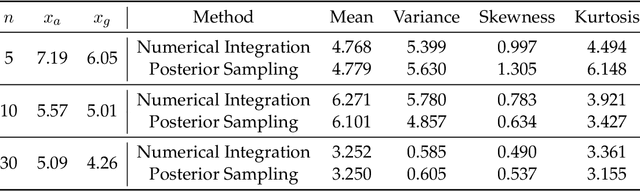
We use the theory of normal variance-mean mixtures to derive a data augmentation scheme for models that include gamma functions. Our methodology applies to many situations in statistics and machine learning, including Multinomial-Dirichlet distributions, Negative binomial regression, Poisson-Gamma hierarchical models, Extreme value models, to name but a few. All of those models include a gamma function which does not admit a natural conjugate prior distribution providing a significant challenge to inference and prediction. To provide a data augmentation strategy, we construct and develop the theory of the class of Exponential Reciprocal Gamma distributions. This allows scalable EM and MCMC algorithms to be developed. We illustrate our methodology on a number of examples, including gamma shape inference, negative binomial regression and Dirichlet allocation. Finally, we conclude with directions for future research.

Bayesian Inference for Polya Inverse Gamma Models

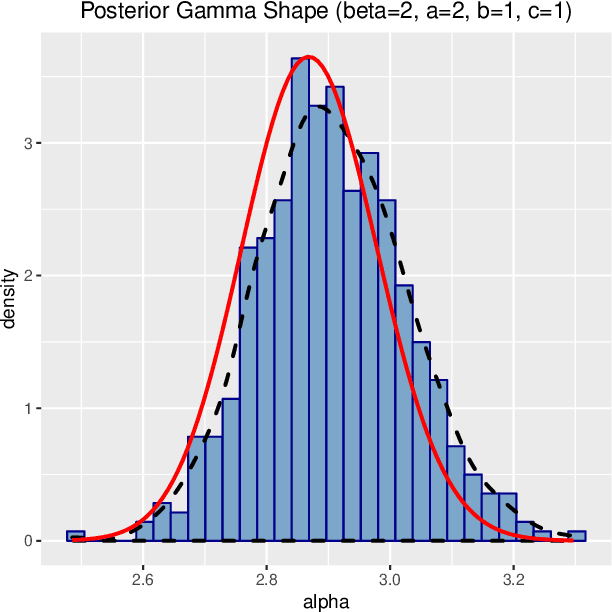
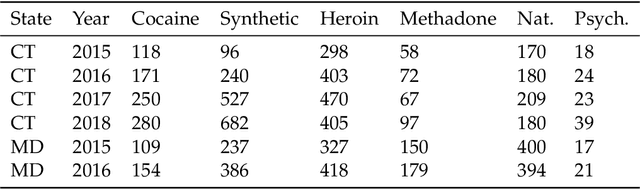
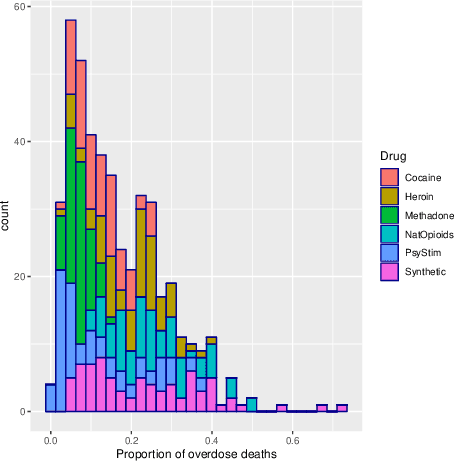
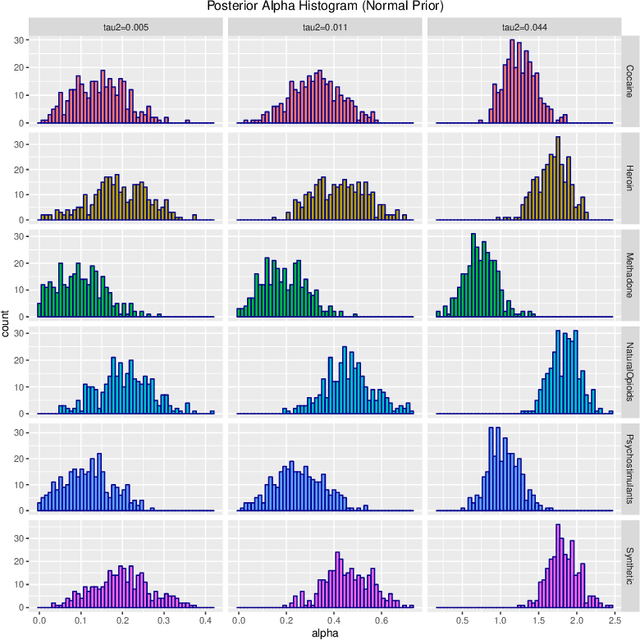
Probability density functions that include the gamma function are widely used in statistics and machine learning. The normalizing constants of gamma, inverse gamma, beta, and Dirichlet distributions all include model parameters as arguments in the gamma function; however, the gamma function does not naturally admit a conjugate prior distribution in a Bayesian analysis, and statistical inference of these parameters is a significant challenge. In this paper, we construct the Polya-inverse Gamma (P-IG) distribution as an infinite convolution of Generalized inverse Gaussian (GIG) distributions, and we represent the reciprocal gamma function as a scale mixture of normal distributions. As a result, the P-IG distribution yields an efficient data augmentation strategy for fully Bayesian inference on model parameters in gamma, inverse gamma, beta, and Dirichlet distributions. To illustrate the applied utility of our data augmentation strategy, we infer the proportion of overdose deaths in the United States attributed to different opioid and prescription drugs with a Dirichlet allocation model.