Stochastic Tree Ensembles for Estimating Heterogeneous Effects

Determining subgroups that respond especially well (or poorly) to specific interventions (medical or policy) requires new supervised learning methods tailored specifically for causal inference. Bayesian Causal Forest (BCF) is a recent method that has been documented to perform well on data generating processes with strong confounding of the sort that is plausible in many applications. This paper develops a novel algorithm for fitting the BCF model, which is more efficient than the previously available Gibbs sampler. The new algorithm can be used to initialize independent chains of the existing Gibbs sampler leading to better posterior exploration and coverage of the associated interval estimates in simulation studies. The new algorithm is compared to related approaches via simulation studies as well as an empirical analysis.

Local Gaussian process extrapolation for BART models with applications to causal inference

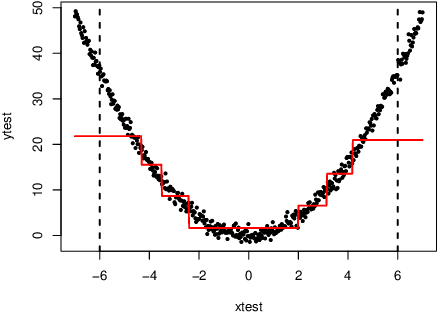
Bayesian additive regression trees (BART) is a semi-parametric regression model offering state-of-the-art performance on out-of-sample prediction. Despite this success, standard implementations of BART typically provide inaccurate prediction and overly narrow prediction intervals at points outside the range of the training data. This paper proposes a novel extrapolation strategy that grafts Gaussian processes to the leaf nodes in BART for predicting points outside the range of the observed data. The new method is compared to standard BART implementations and recent frequentist resampling-based methods for predictive inference. We apply the new approach to a challenging problem from causal inference, wherein for some regions of predictor space, only treated or untreated units are observed (but not both). In simulations studies, the new approach boasts superior performance compared to popular alternatives, such as Jackknife+.

Bayesian Inference for Gamma Models

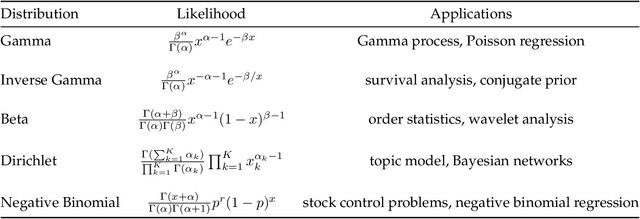
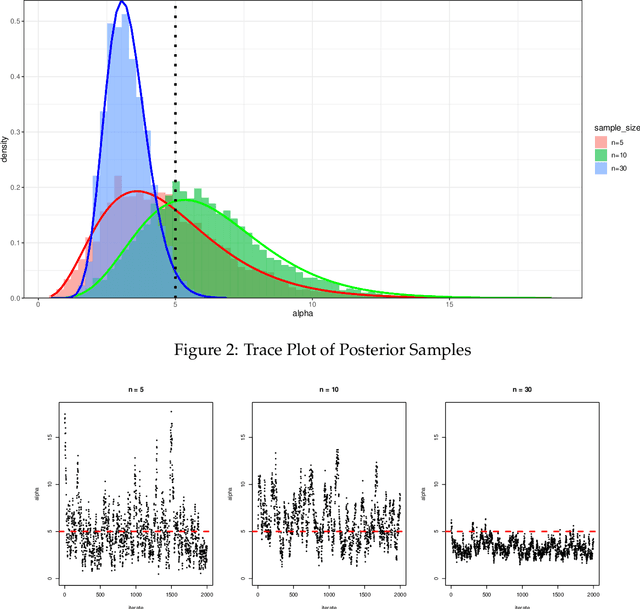
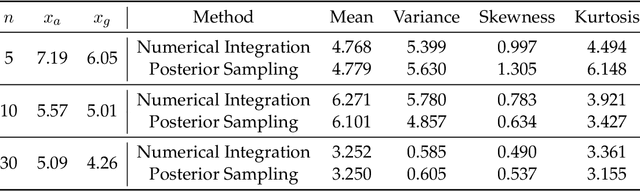
We use the theory of normal variance-mean mixtures to derive a data augmentation scheme for models that include gamma functions. Our methodology applies to many situations in statistics and machine learning, including Multinomial-Dirichlet distributions, Negative binomial regression, Poisson-Gamma hierarchical models, Extreme value models, to name but a few. All of those models include a gamma function which does not admit a natural conjugate prior distribution providing a significant challenge to inference and prediction. To provide a data augmentation strategy, we construct and develop the theory of the class of Exponential Reciprocal Gamma distributions. This allows scalable EM and MCMC algorithms to be developed. We illustrate our methodology on a number of examples, including gamma shape inference, negative binomial regression and Dirichlet allocation. Finally, we conclude with directions for future research.

Stochastic tree ensembles for regularized nonlinear regression

This paper develops a novel stochastic tree ensemble method for nonlinear regression, which we refer to as XBART, short for Accelerated Bayesian Additive Regression Trees. By combining regularization and stochastic search strategies from Bayesian modeling with computationally efficient techniques from recursive partitioning approaches, the new method attains state-of-the-art performance: in many settings it is both faster and more accurate than the widely-used XGBoost algorithm. Via careful simulation studies, we demonstrate that our new approach provides accurate point-wise estimates of the mean function and does so faster than popular alternatives, such as BART, XGBoost and neural networks (using Keras). We also prove a number of basic theoretical results about the new algorithm, including consistency of the single tree version of the model and stationarity of the Markov chain produced by the ensemble version. Furthermore, we demonstrate that initializing standard Bayesian additive regression trees Markov chain Monte Carlo (MCMC) at XBART-fitted trees considerably improves credible interval coverage and reduces total run-time.

Bayesian Inference for Polya Inverse Gamma Models

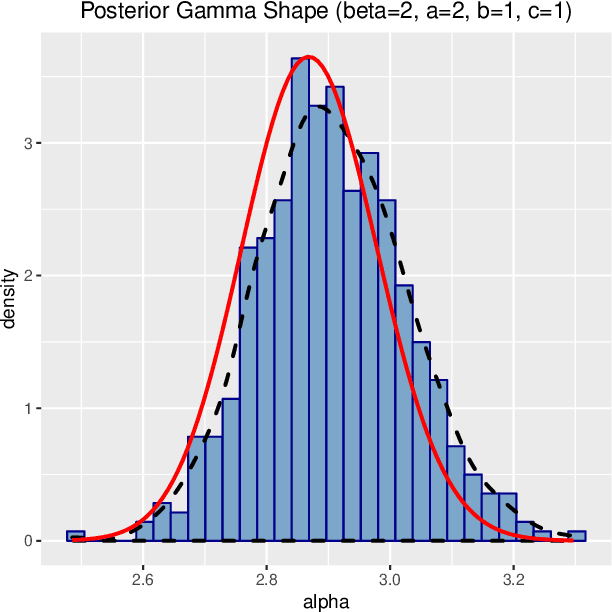
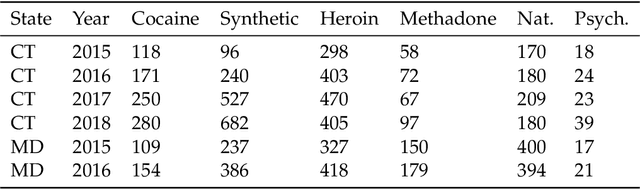
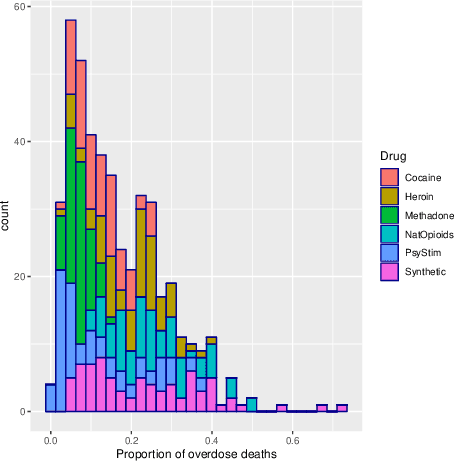
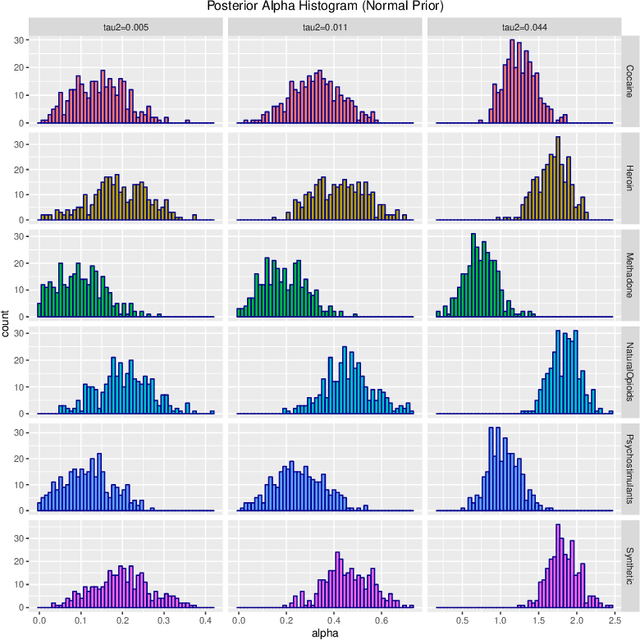
Probability density functions that include the gamma function are widely used in statistics and machine learning. The normalizing constants of gamma, inverse gamma, beta, and Dirichlet distributions all include model parameters as arguments in the gamma function; however, the gamma function does not naturally admit a conjugate prior distribution in a Bayesian analysis, and statistical inference of these parameters is a significant challenge. In this paper, we construct the Polya-inverse Gamma (P-IG) distribution as an infinite convolution of Generalized inverse Gaussian (GIG) distributions, and we represent the reciprocal gamma function as a scale mixture of normal distributions. As a result, the P-IG distribution yields an efficient data augmentation strategy for fully Bayesian inference on model parameters in gamma, inverse gamma, beta, and Dirichlet distributions. To illustrate the applied utility of our data augmentation strategy, we infer the proportion of overdose deaths in the United States attributed to different opioid and prescription drugs with a Dirichlet allocation model.

Efficient sampling for Gaussian linear regression with arbitrary priors

This paper develops a slice sampler for Bayesian linear regression models with arbitrary priors. The new sampler has two advantages over current approaches. One, it is faster than many custom implementations that rely on auxiliary latent variables, if the number of regressors is large. Two, it can be used with any prior with a density function that can be evaluated up to a normalizing constant, making it ideal for investigating the properties of new shrinkage priors without having to develop custom sampling algorithms. The new sampler takes advantage of the special structure of the linear regression likelihood, allowing it to produce better effective sample size per second than common alternative approaches.

Deep Learning for Predicting Asset Returns

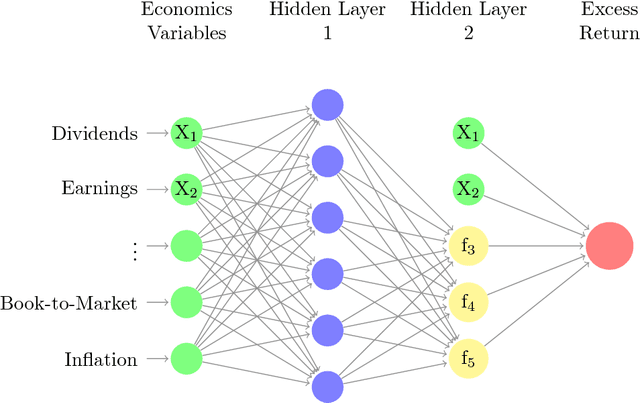
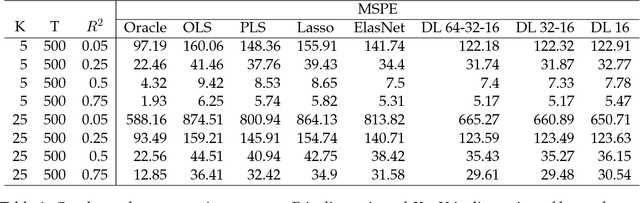
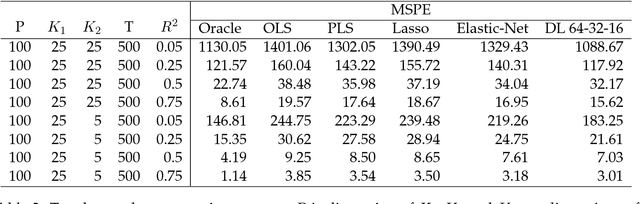
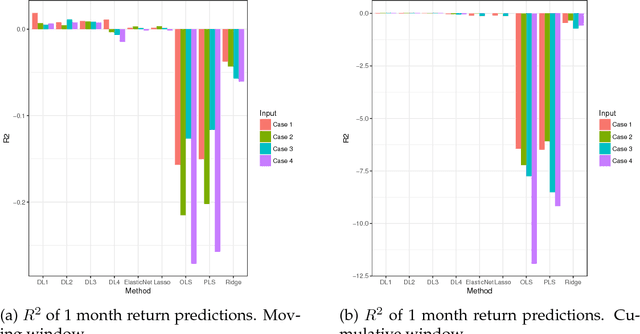
Deep learning searches for nonlinear factors for predicting asset returns. Predictability is achieved via multiple layers of composite factors as opposed to additive ones. Viewed in this way, asset pricing studies can be revisited using multi-layer deep learners, such as rectified linear units (ReLU) or long-short-term-memory (LSTM) for time-series effects. State-of-the-art algorithms including stochastic gradient descent (SGD), TensorFlow and dropout design provide imple- mentation and efficient factor exploration. To illustrate our methodology, we revisit the equity market risk premium dataset of Welch and Goyal (2008). We find the existence of nonlinear factors which explain predictability of returns, in particular at the extremes of the characteristic space. Finally, we conclude with directions for future research.