Growing the Efficient Frontier on Panel Trees

We introduce a new class of tree-based models, P-Trees, for analyzing (unbalanced) panel of individual asset returns, generalizing high-dimensional sorting with economic guidance and interpretability. Under the mean-variance efficient framework, P-Trees construct test assets that significantly advance the efficient frontier compared to commonly used test assets, with alphas unexplained by benchmark pricing models. P-Tree tangency portfolios also constitute traded factors, recovering the pricing kernel and outperforming popular observable and latent factor models for investments and cross-sectional pricing. Finally, P-Trees capture the complexity of asset returns with sparsity, achieving out-of-sample Sharpe ratios close to those attained only by over-parameterized large models.

Deep Learning for Predicting Asset Returns

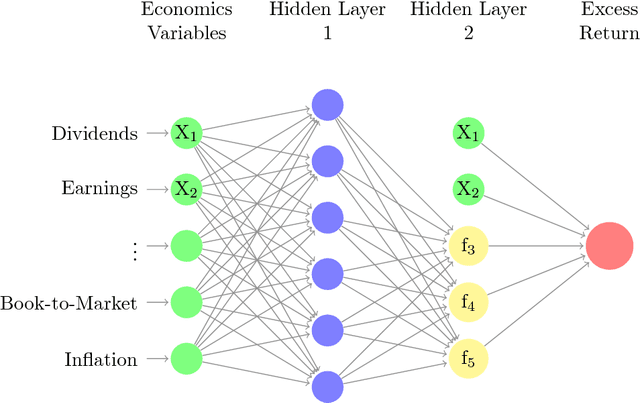
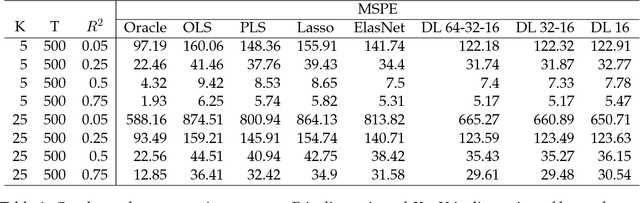
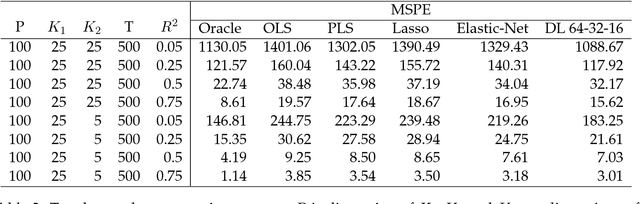
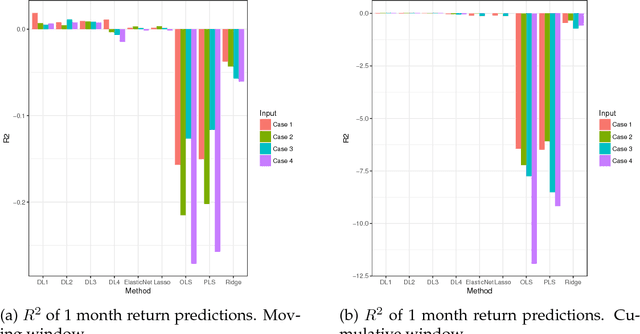
Deep learning searches for nonlinear factors for predicting asset returns. Predictability is achieved via multiple layers of composite factors as opposed to additive ones. Viewed in this way, asset pricing studies can be revisited using multi-layer deep learners, such as rectified linear units (ReLU) or long-short-term-memory (LSTM) for time-series effects. State-of-the-art algorithms including stochastic gradient descent (SGD), TensorFlow and dropout design provide imple- mentation and efficient factor exploration. To illustrate our methodology, we revisit the equity market risk premium dataset of Welch and Goyal (2008). We find the existence of nonlinear factors which explain predictability of returns, in particular at the extremes of the characteristic space. Finally, we conclude with directions for future research.