Prediction-Powered Inference with Inverse Probability Weighting

Prediction-powered inference (PPI) is a recent framework for valid statistical inference with partially labeled data, combining model-based predictions on a large unlabeled set with bias correction from a smaller labeled subset. We show that PPI can be extended to handle informative labeling by replacing its unweighted bias-correction term with an inverse probability weighted (IPW) version, using the classical Horvitz--Thompson or H\'ajek forms. This connection unites design-based survey sampling ideas with modern prediction-assisted inference, yielding estimators that remain valid when labeling probabilities vary across units. We consider the common setting where the inclusion probabilities are not known but estimated from a correctly specified model. In simulations, the performance of IPW-adjusted PPI with estimated propensities closely matches the known-probability case, retaining both nominal coverage and the variance-reduction benefits of PPI.

Bayesian Deep ICE

Deep Independent Component Estimation (DICE) has many applications in modern day machine learning as a feature engineering extraction method. We provide a novel latent variable representation of independent component analysis that enables both point estimates via expectation-maximization (EM) and full posterior sampling via Markov Chain Monte Carlo (MCMC) algorithms. Our methodology also applies to flow-based methods for nonlinear feature extraction. We discuss how to implement conditional posteriors and envelope-based methods for optimization. Through this representation hierarchy, we unify a number of hitherto disjoint estimation procedures. We illustrate our methodology and algorithms on a numerical example. Finally, we conclude with directions for future research.

Deep Partial Least Squares for Empirical Asset Pricing

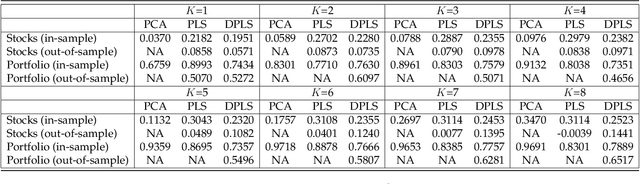
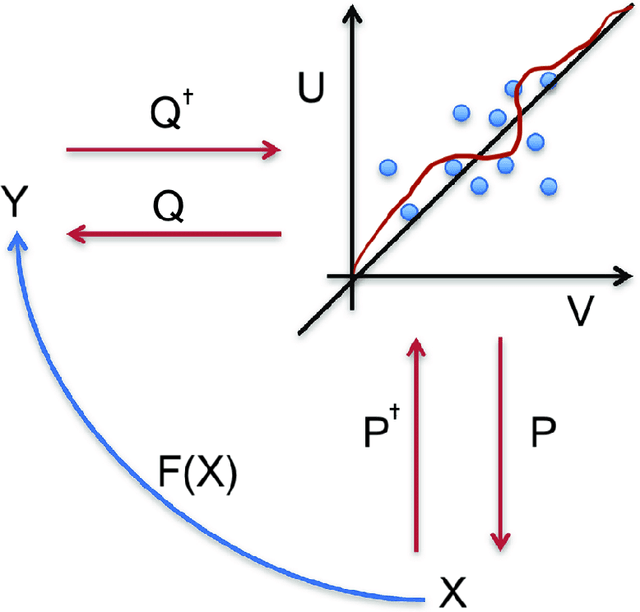
We use deep partial least squares (DPLS) to estimate an asset pricing model for individual stock returns that exploits conditioning information in a flexible and dynamic way while attributing excess returns to a small set of statistical risk factors. The novel contribution is to resolve the non-linear factor structure, thus advancing the current paradigm of deep learning in empirical asset pricing which uses linear stochastic discount factors under an assumption of Gaussian asset returns and factors. This non-linear factor structure is extracted by using projected least squares to jointly project firm characteristics and asset returns on to a subspace of latent factors and using deep learning to learn the non-linear map from the factor loadings to the asset returns. The result of capturing this non-linear risk factor structure is to characterize anomalies in asset returns by both linear risk factor exposure and interaction effects. Thus the well known ability of deep learning to capture outliers, shed lights on the role of convexity and higher order terms in the latent factor structure on the factor risk premia. On the empirical side, we implement our DPLS factor models and exhibit superior performance to LASSO and plain vanilla deep learning models. Furthermore, our network training times are significantly reduced due to the more parsimonious architecture of DPLS. Specifically, using 3290 assets in the Russell 1000 index over a period of December 1989 to January 2018, we assess our DPLS factor model and generate information ratios that are approximately 1.2x greater than deep learning. DPLS explains variation and pricing errors and identifies the most prominent latent factors and firm characteristics.

Bayesian Inference for Polya Inverse Gamma Models

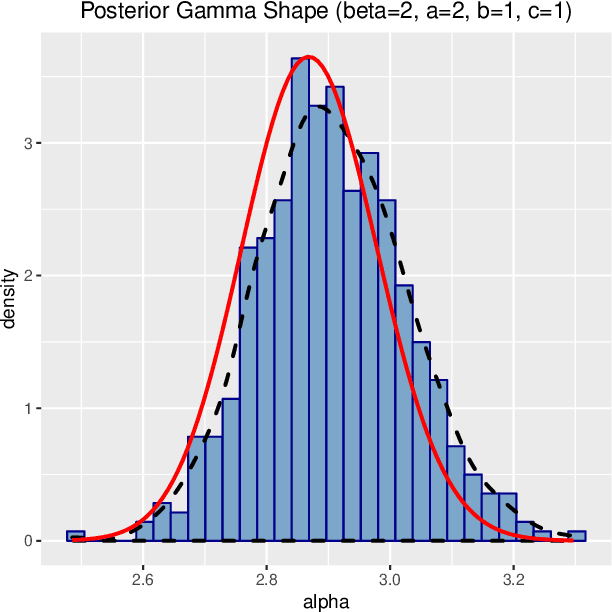
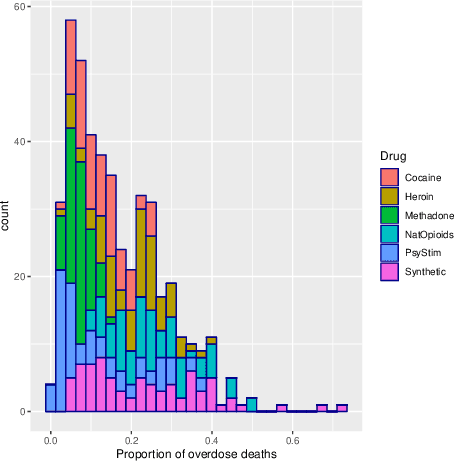
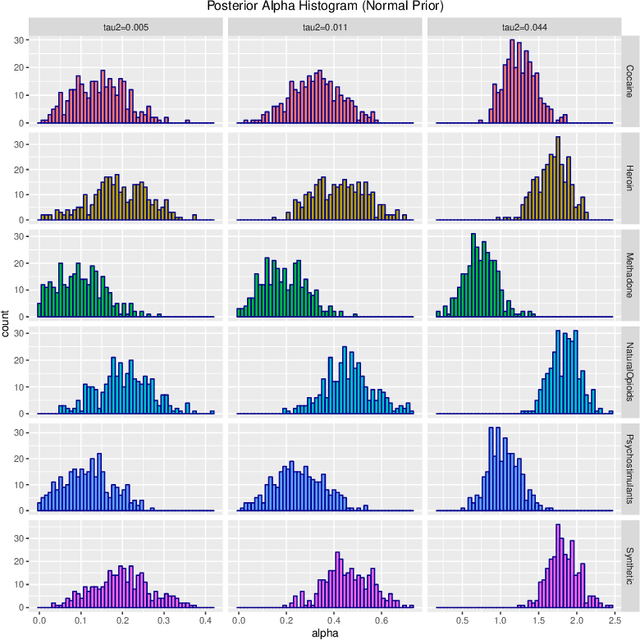
Probability density functions that include the gamma function are widely used in statistics and machine learning. The normalizing constants of gamma, inverse gamma, beta, and Dirichlet distributions all include model parameters as arguments in the gamma function; however, the gamma function does not naturally admit a conjugate prior distribution in a Bayesian analysis, and statistical inference of these parameters is a significant challenge. In this paper, we construct the Polya-inverse Gamma (P-IG) distribution as an infinite convolution of Generalized inverse Gaussian (GIG) distributions, and we represent the reciprocal gamma function as a scale mixture of normal distributions. As a result, the P-IG distribution yields an efficient data augmentation strategy for fully Bayesian inference on model parameters in gamma, inverse gamma, beta, and Dirichlet distributions. To illustrate the applied utility of our data augmentation strategy, we infer the proportion of overdose deaths in the United States attributed to different opioid and prescription drugs with a Dirichlet allocation model.

Horseshoe Regularization for Machine Learning in Complex and Deep Models

Since the advent of the horseshoe priors for regularization, global-local shrinkage methods have proved to be a fertile ground for the development of Bayesian methodology in machine learning, specifically for high-dimensional regression and classification problems. They have achieved remarkable success in computation, and enjoy strong theoretical support. Most of the existing literature has focused on the linear Gaussian case; see Bhadra et al. (2019) for a systematic survey. The purpose of the current article is to demonstrate that the horseshoe regularization is useful far more broadly, by reviewing both methodological and computational developments in complex models that are more relevant to machine learning applications. Specifically, we focus on methodological challenges in horseshoe regularization in nonlinear and non-Gaussian models; multivariate models; and deep neural networks. We also outline the recent computational developments in horseshoe shrinkage for complex models along with a list of available software implementations that allows one to venture out beyond the comfort zone of the canonical linear regression problems.

Scalable Data Augmentation for Deep Learning

Scalable Data Augmentation (SDA) provides a framework for training deep learning models using auxiliary hidden layers. Scalable MCMC is available for network training and inference. SDA provides a number of computational advantages over traditional algorithms, such as avoiding backtracking, local modes and can perform optimization with stochastic gradient descent (SGD) in TensorFlow. Standard deep neural networks with logit, ReLU and SVM activation functions are straightforward to implement. To illustrate our architectures and methodology, we use P\'{o}lya-Gamma logit data augmentation for a number of standard datasets. Finally, we conclude with directions for future research.

Deep Fundamental Factor Models

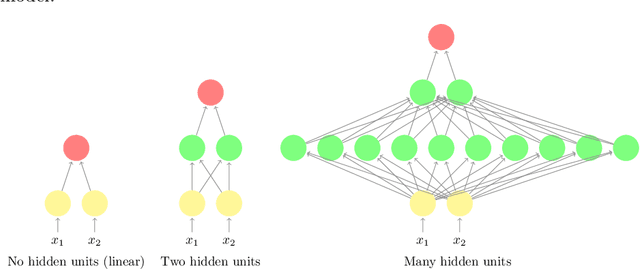
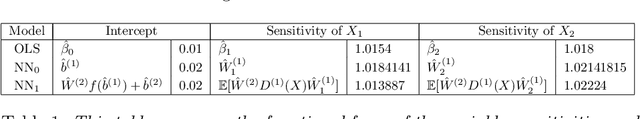
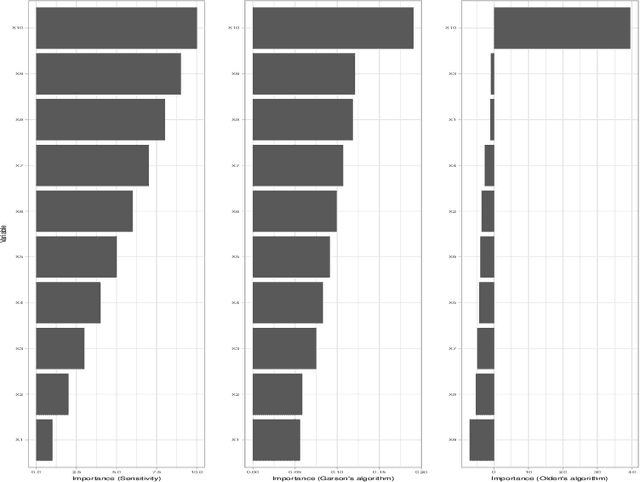
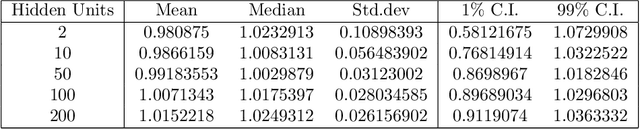
Deep fundamental factor models are developed to interpret and capture non-linearity, interaction effects and non-parametric shocks in financial econometrics. Uncertainty quantification provides interpretability with interval estimation, ranking of factor importances and estimation of interaction effects. Estimating factor realizations under either homoscedastic or heteroscedastic error is also available. With no hidden layers we recover a linear factor model and for one or more hidden layers, uncertainty bands for the sensitivity to each input naturally arise from the network weights. To illustrate our methodology, we construct a six-factor model of assets in the S\&P 500 index and generate information ratios that are three times greater than generalized linear regression. We show that the factor importances are materially different from the linear factor model when accounting for non-linearity. Finally, we conclude with directions for future research

Deep Learning

Deep learning (DL) is a high dimensional data reduction technique for constructing high-dimensional predictors in input-output models. DL is a form of machine learning that uses hierarchical layers of latent features. In this article, we review the state-of-the-art of deep learning from a modeling and algorithmic perspective. We provide a list of successful areas of applications in Artificial Intelligence (AI), Image Processing, Robotics and Automation. Deep learning is predictive in its nature rather then inferential and can be viewed as a black-box methodology for high-dimensional function estimation.

Deep Learning for Spatio-Temporal Modeling: Dynamic Traffic Flows and High Frequency Trading

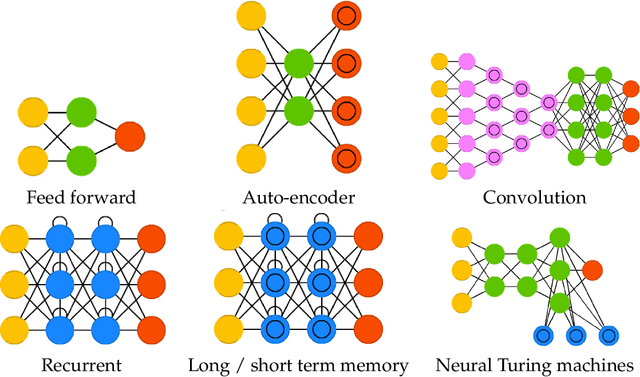
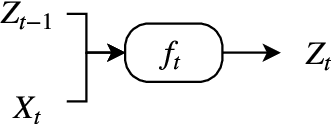
Deep learning applies hierarchical layers of hidden variables to construct nonlinear high dimensional predictors. Our goal is to develop and train deep learning architectures for spatio-temporal modeling. Training a deep architecture is achieved by stochastic gradient descent (SGD) and drop-out (DO) for parameter regularization with a goal of minimizing out-of-sample predictive mean squared error. To illustrate our methodology, we predict the sharp discontinuities in traffic flow data, and secondly, we develop a classification rule to predict short-term futures market prices as a function of the order book depth. Finally, we conclude with directions for future research.

Deep Learning for Predicting Asset Returns

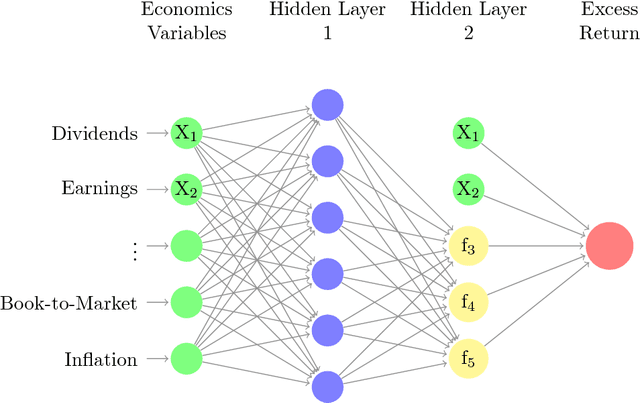
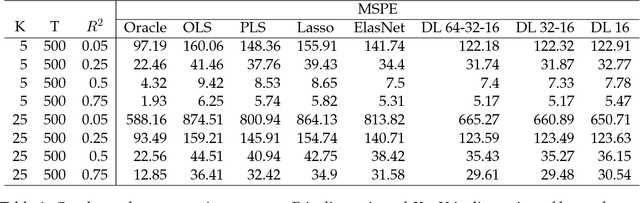
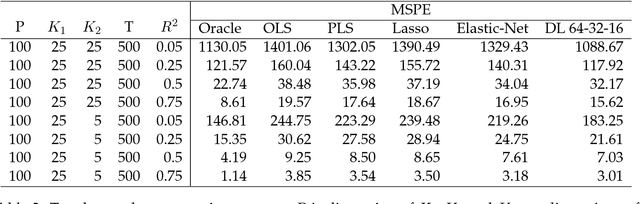
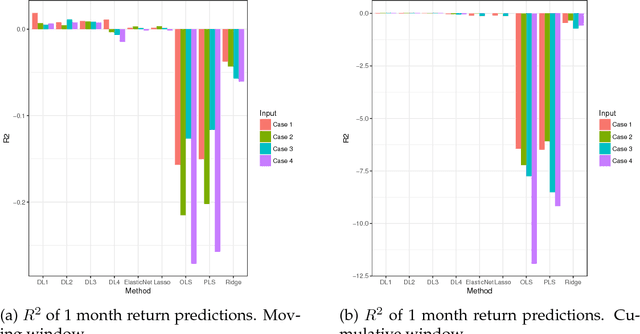
Deep learning searches for nonlinear factors for predicting asset returns. Predictability is achieved via multiple layers of composite factors as opposed to additive ones. Viewed in this way, asset pricing studies can be revisited using multi-layer deep learners, such as rectified linear units (ReLU) or long-short-term-memory (LSTM) for time-series effects. State-of-the-art algorithms including stochastic gradient descent (SGD), TensorFlow and dropout design provide imple- mentation and efficient factor exploration. To illustrate our methodology, we revisit the equity market risk premium dataset of Welch and Goyal (2008). We find the existence of nonlinear factors which explain predictability of returns, in particular at the extremes of the characteristic space. Finally, we conclude with directions for future research.