Deep Partial Least Squares for Empirical Asset Pricing

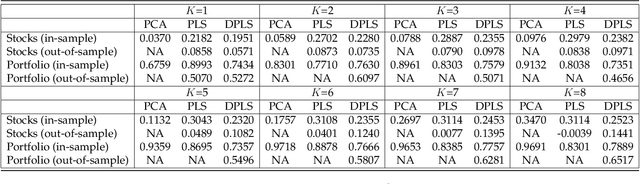
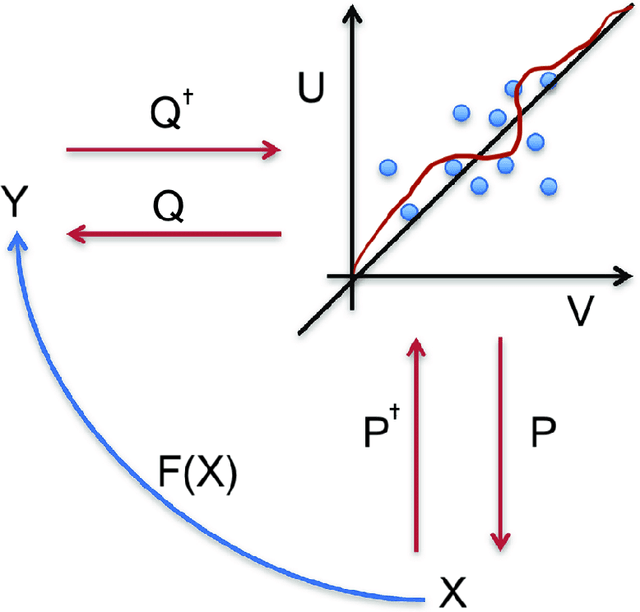
We use deep partial least squares (DPLS) to estimate an asset pricing model for individual stock returns that exploits conditioning information in a flexible and dynamic way while attributing excess returns to a small set of statistical risk factors. The novel contribution is to resolve the non-linear factor structure, thus advancing the current paradigm of deep learning in empirical asset pricing which uses linear stochastic discount factors under an assumption of Gaussian asset returns and factors. This non-linear factor structure is extracted by using projected least squares to jointly project firm characteristics and asset returns on to a subspace of latent factors and using deep learning to learn the non-linear map from the factor loadings to the asset returns. The result of capturing this non-linear risk factor structure is to characterize anomalies in asset returns by both linear risk factor exposure and interaction effects. Thus the well known ability of deep learning to capture outliers, shed lights on the role of convexity and higher order terms in the latent factor structure on the factor risk premia. On the empirical side, we implement our DPLS factor models and exhibit superior performance to LASSO and plain vanilla deep learning models. Furthermore, our network training times are significantly reduced due to the more parsimonious architecture of DPLS. Specifically, using 3290 assets in the Russell 1000 index over a period of December 1989 to January 2018, we assess our DPLS factor model and generate information ratios that are approximately 1.2x greater than deep learning. DPLS explains variation and pricing errors and identifies the most prominent latent factors and firm characteristics.

Deep Fundamental Factor Models

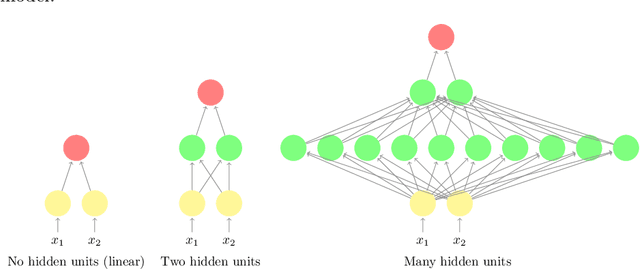
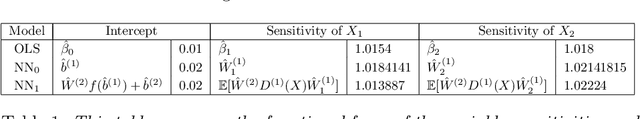
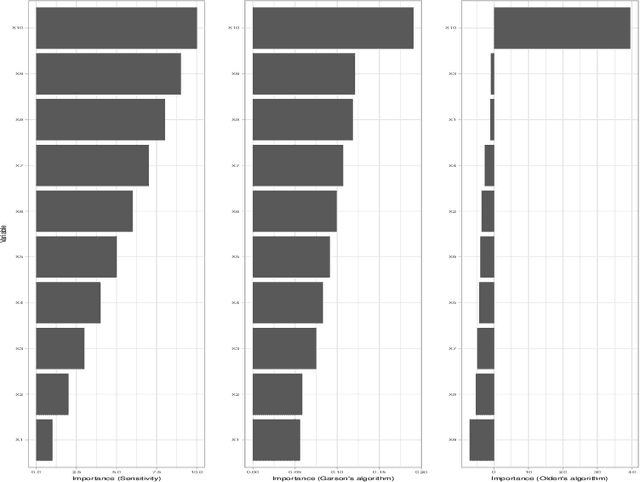
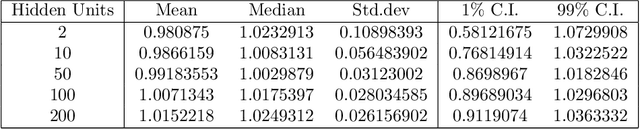
Deep fundamental factor models are developed to interpret and capture non-linearity, interaction effects and non-parametric shocks in financial econometrics. Uncertainty quantification provides interpretability with interval estimation, ranking of factor importances and estimation of interaction effects. Estimating factor realizations under either homoscedastic or heteroscedastic error is also available. With no hidden layers we recover a linear factor model and for one or more hidden layers, uncertainty bands for the sensitivity to each input naturally arise from the network weights. To illustrate our methodology, we construct a six-factor model of assets in the S\&P 500 index and generate information ratios that are three times greater than generalized linear regression. We show that the factor importances are materially different from the linear factor model when accounting for non-linearity. Finally, we conclude with directions for future research

Deep Learning for Spatio-Temporal Modeling: Dynamic Traffic Flows and High Frequency Trading

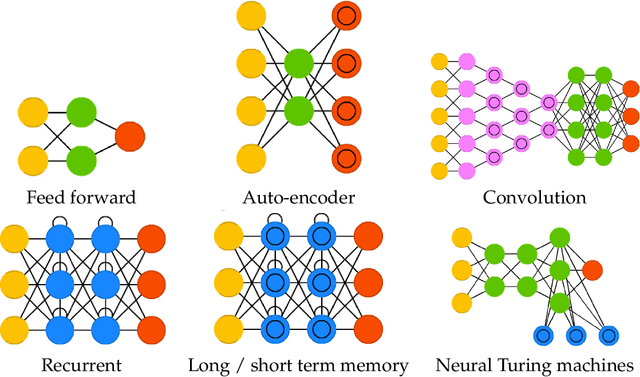
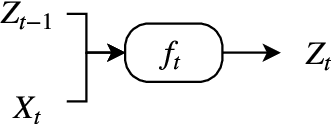
Deep learning applies hierarchical layers of hidden variables to construct nonlinear high dimensional predictors. Our goal is to develop and train deep learning architectures for spatio-temporal modeling. Training a deep architecture is achieved by stochastic gradient descent (SGD) and drop-out (DO) for parameter regularization with a goal of minimizing out-of-sample predictive mean squared error. To illustrate our methodology, we predict the sharp discontinuities in traffic flow data, and secondly, we develop a classification rule to predict short-term futures market prices as a function of the order book depth. Finally, we conclude with directions for future research.