Bayesian Inference for Polya Inverse Gamma Models
Paper and Code
May 29, 2019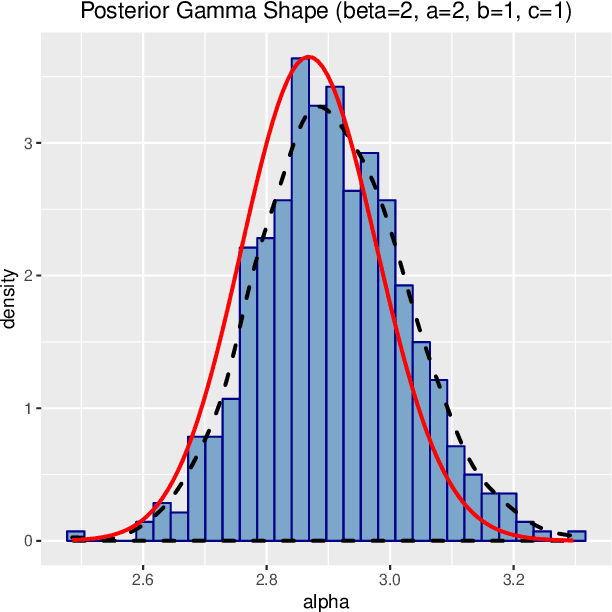
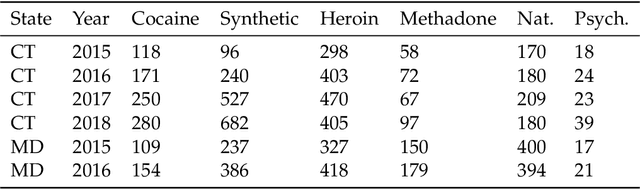
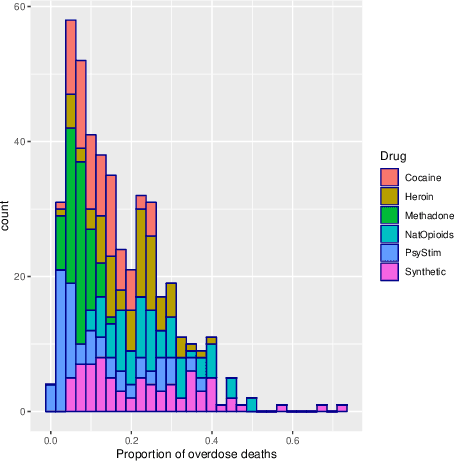
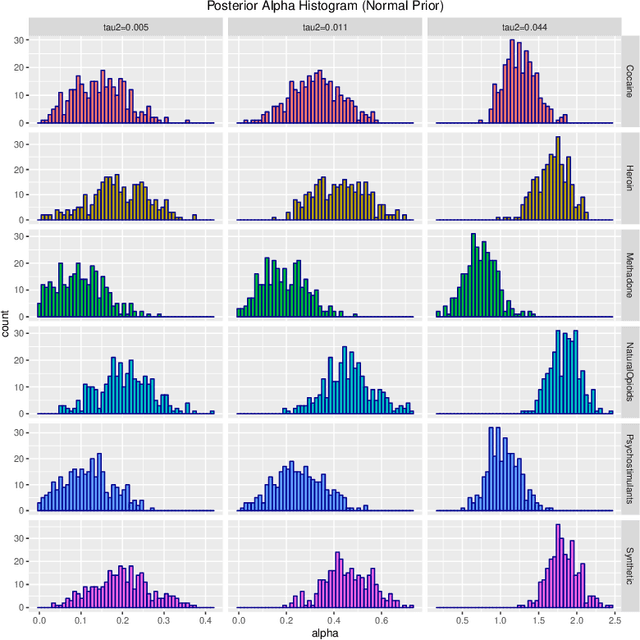
Probability density functions that include the gamma function are widely used in statistics and machine learning. The normalizing constants of gamma, inverse gamma, beta, and Dirichlet distributions all include model parameters as arguments in the gamma function; however, the gamma function does not naturally admit a conjugate prior distribution in a Bayesian analysis, and statistical inference of these parameters is a significant challenge. In this paper, we construct the Polya-inverse Gamma (P-IG) distribution as an infinite convolution of Generalized inverse Gaussian (GIG) distributions, and we represent the reciprocal gamma function as a scale mixture of normal distributions. As a result, the P-IG distribution yields an efficient data augmentation strategy for fully Bayesian inference on model parameters in gamma, inverse gamma, beta, and Dirichlet distributions. To illustrate the applied utility of our data augmentation strategy, we infer the proportion of overdose deaths in the United States attributed to different opioid and prescription drugs with a Dirichlet allocation model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge