Deep Learning for Causal Inference: A Comparison of Architectures for Heterogeneous Treatment Effect Estimation

Causal inference has gained much popularity in recent years, with interests ranging from academic, to industrial, to educational, and all in between. Concurrently, the study and usage of neural networks has also grown profoundly (albeit at a far faster rate). What we aim to do in this blog write-up is demonstrate a Neural Network causal inference architecture. We develop a fully connected neural network implementation of the popular Bayesian Causal Forest algorithm, a state of the art tree based method for estimating heterogeneous treatment effects. We compare our implementation to existing neural network causal inference methodologies, showing improvements in performance in simulation settings. We apply our method to a dataset examining the effect of stress on sleep.

Feature selection in stratification estimators of causal effects: lessons from potential outcomes, causal diagrams, and structural equations

What is the ideal regression (if any) for estimating average causal effects? We study this question in the setting of discrete covariates, deriving expressions for the finite-sample variance of various stratification estimators. This approach clarifies the fundamental statistical phenomena underlying many widely-cited results. Our exposition combines insights from three distinct methodological traditions for studying causal effect estimation: potential outcomes, causal diagrams, and structural models with additive errors.

Stochastic Tree Ensembles for Estimating Heterogeneous Effects

Determining subgroups that respond especially well (or poorly) to specific interventions (medical or policy) requires new supervised learning methods tailored specifically for causal inference. Bayesian Causal Forest (BCF) is a recent method that has been documented to perform well on data generating processes with strong confounding of the sort that is plausible in many applications. This paper develops a novel algorithm for fitting the BCF model, which is more efficient than the previously available Gibbs sampler. The new algorithm can be used to initialize independent chains of the existing Gibbs sampler leading to better posterior exploration and coverage of the associated interval estimates in simulation studies. The new algorithm is compared to related approaches via simulation studies as well as an empirical analysis.

Statistical Aspects of SHAP: Functional ANOVA for Model Interpretation

SHAP is a popular method for measuring variable importance in machine learning models. In this paper, we study the algorithm used to estimate SHAP scores and show that it is a transformation of the functional ANOVA decomposition. We use this connection to show that challenges in SHAP approximations largely relate to the choice of a feature distribution and the number of $2^p$ ANOVA terms estimated. We argue that the connection between machine learning explainability and sensitivity analysis is illuminating in this case, but the immediate practical consequences are not obvious since the two fields face a different set of constraints. Machine learning explainability concerns models which are inexpensive to evaluate but often have hundreds, if not thousands, of features. Sensitivity analysis typically deals with models from physics or engineering which may be very time consuming to run, but operate on a comparatively small space of inputs.

Local Gaussian process extrapolation for BART models with applications to causal inference

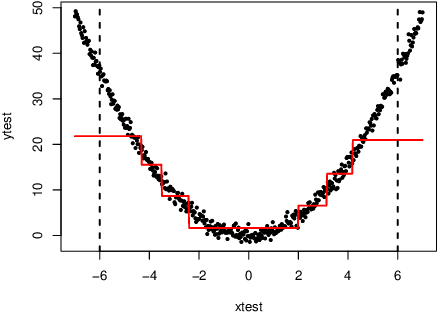
Bayesian additive regression trees (BART) is a semi-parametric regression model offering state-of-the-art performance on out-of-sample prediction. Despite this success, standard implementations of BART typically provide inaccurate prediction and overly narrow prediction intervals at points outside the range of the training data. This paper proposes a novel extrapolation strategy that grafts Gaussian processes to the leaf nodes in BART for predicting points outside the range of the observed data. The new method is compared to standard BART implementations and recent frequentist resampling-based methods for predictive inference. We apply the new approach to a challenging problem from causal inference, wherein for some regions of predictor space, only treated or untreated units are observed (but not both). In simulations studies, the new approach boasts superior performance compared to popular alternatives, such as Jackknife+.

Semi-supervised learning and the question of true versus estimated propensity scores

A straightforward application of semi-supervised machine learning to the problem of treatment effect estimation would be to consider data as "unlabeled" if treatment assignment and covariates are observed but outcomes are unobserved. According to this formulation, large unlabeled data sets could be used to estimate a high dimensional propensity function and causal inference using a much smaller labeled data set could proceed via weighted estimators using the learned propensity scores. In the limiting case of infinite unlabeled data, one may estimate the high dimensional propensity function exactly. However, longstanding advice in the causal inference community suggests that estimated propensity scores (from labeled data alone) are actually preferable to true propensity scores, implying that the unlabeled data is actually useless in this context. In this paper we examine this paradox and propose a simple procedure that reconciles the strong intuition that a known propensity functions should be useful for estimating treatment effects with the previous literature suggesting otherwise. Further, simulation studies suggest that direct regression may be preferable to inverse-propensity weight estimators in many circumstances.

Stochastic tree ensembles for regularized nonlinear regression

This paper develops a novel stochastic tree ensemble method for nonlinear regression, which we refer to as XBART, short for Accelerated Bayesian Additive Regression Trees. By combining regularization and stochastic search strategies from Bayesian modeling with computationally efficient techniques from recursive partitioning approaches, the new method attains state-of-the-art performance: in many settings it is both faster and more accurate than the widely-used XGBoost algorithm. Via careful simulation studies, we demonstrate that our new approach provides accurate point-wise estimates of the mean function and does so faster than popular alternatives, such as BART, XGBoost and neural networks (using Keras). We also prove a number of basic theoretical results about the new algorithm, including consistency of the single tree version of the model and stationarity of the Markov chain produced by the ensemble version. Furthermore, we demonstrate that initializing standard Bayesian additive regression trees Markov chain Monte Carlo (MCMC) at XBART-fitted trees considerably improves credible interval coverage and reduces total run-time.

A Survey of Learning Causality with Data: Problems and Methods

The era of big data provides researchers with convenient access to copious data. However, people often have little knowledge about it. The increasing prevalence of big data is challenging the traditional methods of learning causality because they are developed for the cases with limited amount of data and solid prior causal knowledge. This survey aims to close the gap between big data and learning causality with a comprehensive and structured review of traditional and frontier methods and a discussion about some open problems of learning causality. We begin with preliminaries of learning causality. Then we categorize and revisit methods of learning causality for the typical problems and data types. After that, we discuss the connections between learning causality and machine learning. At the end, some open problems are presented to show the great potential of learning causality with data.

Efficient sampling for Gaussian linear regression with arbitrary priors

This paper develops a slice sampler for Bayesian linear regression models with arbitrary priors. The new sampler has two advantages over current approaches. One, it is faster than many custom implementations that rely on auxiliary latent variables, if the number of regressors is large. Two, it can be used with any prior with a density function that can be evaluated up to a normalizing constant, making it ideal for investigating the properties of new shrinkage priors without having to develop custom sampling algorithms. The new sampler takes advantage of the special structure of the linear regression likelihood, allowing it to produce better effective sample size per second than common alternative approaches.

A Structural Approach to Coordinate-Free Statistics

We consider the question of learning in general topological vector spaces. By exploiting known (or parametrized) covariance structures, our Main Theorem demonstrates that any continuous linear map corresponds to a certain isomorphism of embedded Hilbert spaces. By inverting this isomorphism and extending continuously, we construct a version of the Ordinary Least Squares estimator in absolute generality. Our Gauss-Markov theorem demonstrates that OLS is a "best linear unbiased estimator", extending the classical result. We construct a stochastic version of the OLS estimator, which is a continuous disintegration exactly for the class of "uncorrelated implies independent" (UII) measures. As a consequence, Gaussian measures always exhibit continuous disintegrations through continuous linear maps, extending a theorem of the first author. Applying this framework to some problems in machine learning, we prove a useful representation theorem for covariance tensors, and show that OLS defines a good kriging predictor for vector-valued arrays on general index spaces. We also construct a support-vector machine classifier in this setting. We hope that our article shines light on some deeper connections between probability theory, statistics and machine learning, and may serve as a point of intersection for these three communities.