Tom LaGatta
Conscientious Classification: A Data Scientist's Guide to Discrimination-Aware Classification
Jul 21, 2019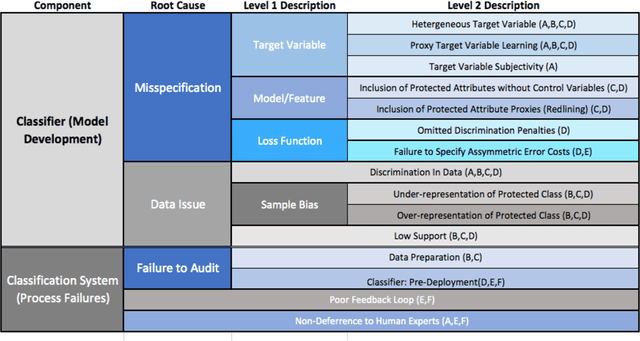
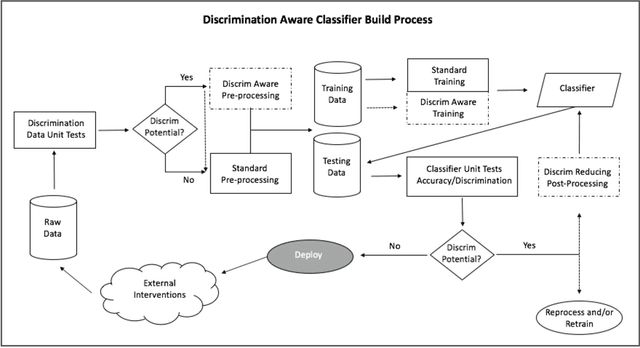
Abstract:Recent research has helped to cultivate growing awareness that machine learning systems fueled by big data can create or exacerbate troubling disparities in society. Much of this research comes from outside of the practicing data science community, leaving its members with little concrete guidance to proactively address these concerns. This article introduces issues of discrimination to the data science community on its own terms. In it, we tour the familiar data mining process while providing a taxonomy of common practices that have the potential to produce unintended discrimination. We also survey how discrimination is commonly measured, and suggest how familiar development processes can be augmented to mitigate systems' discriminatory potential. We advocate that data scientists should be intentional about modeling and reducing discriminatory outcomes. Without doing so, their efforts will result in perpetuating any systemic discrimination that may exist, but under a misleading veil of data-driven objectivity.
* 30 pages, 3 figures
A Structural Approach to Coordinate-Free Statistics
May 05, 2014Abstract:We consider the question of learning in general topological vector spaces. By exploiting known (or parametrized) covariance structures, our Main Theorem demonstrates that any continuous linear map corresponds to a certain isomorphism of embedded Hilbert spaces. By inverting this isomorphism and extending continuously, we construct a version of the Ordinary Least Squares estimator in absolute generality. Our Gauss-Markov theorem demonstrates that OLS is a "best linear unbiased estimator", extending the classical result. We construct a stochastic version of the OLS estimator, which is a continuous disintegration exactly for the class of "uncorrelated implies independent" (UII) measures. As a consequence, Gaussian measures always exhibit continuous disintegrations through continuous linear maps, extending a theorem of the first author. Applying this framework to some problems in machine learning, we prove a useful representation theorem for covariance tensors, and show that OLS defines a good kriging predictor for vector-valued arrays on general index spaces. We also construct a support-vector machine classifier in this setting. We hope that our article shines light on some deeper connections between probability theory, statistics and machine learning, and may serve as a point of intersection for these three communities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge