Deep Learning for Causal Inference: A Comparison of Architectures for Heterogeneous Treatment Effect Estimation

Causal inference has gained much popularity in recent years, with interests ranging from academic, to industrial, to educational, and all in between. Concurrently, the study and usage of neural networks has also grown profoundly (albeit at a far faster rate). What we aim to do in this blog write-up is demonstrate a Neural Network causal inference architecture. We develop a fully connected neural network implementation of the popular Bayesian Causal Forest algorithm, a state of the art tree based method for estimating heterogeneous treatment effects. We compare our implementation to existing neural network causal inference methodologies, showing improvements in performance in simulation settings. We apply our method to a dataset examining the effect of stress on sleep.

Feature selection in stratification estimators of causal effects: lessons from potential outcomes, causal diagrams, and structural equations

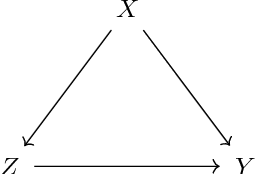
What is the ideal regression (if any) for estimating average causal effects? We study this question in the setting of discrete covariates, deriving expressions for the finite-sample variance of various stratification estimators. This approach clarifies the fundamental statistical phenomena underlying many widely-cited results. Our exposition combines insights from three distinct methodological traditions for studying causal effect estimation: potential outcomes, causal diagrams, and structural models with additive errors.

Statistical Aspects of SHAP: Functional ANOVA for Model Interpretation

SHAP is a popular method for measuring variable importance in machine learning models. In this paper, we study the algorithm used to estimate SHAP scores and show that it is a transformation of the functional ANOVA decomposition. We use this connection to show that challenges in SHAP approximations largely relate to the choice of a feature distribution and the number of $2^p$ ANOVA terms estimated. We argue that the connection between machine learning explainability and sensitivity analysis is illuminating in this case, but the immediate practical consequences are not obvious since the two fields face a different set of constraints. Machine learning explainability concerns models which are inexpensive to evaluate but often have hundreds, if not thousands, of features. Sensitivity analysis typically deals with models from physics or engineering which may be very time consuming to run, but operate on a comparatively small space of inputs.

Semi-supervised learning and the question of true versus estimated propensity scores

A straightforward application of semi-supervised machine learning to the problem of treatment effect estimation would be to consider data as "unlabeled" if treatment assignment and covariates are observed but outcomes are unobserved. According to this formulation, large unlabeled data sets could be used to estimate a high dimensional propensity function and causal inference using a much smaller labeled data set could proceed via weighted estimators using the learned propensity scores. In the limiting case of infinite unlabeled data, one may estimate the high dimensional propensity function exactly. However, longstanding advice in the causal inference community suggests that estimated propensity scores (from labeled data alone) are actually preferable to true propensity scores, implying that the unlabeled data is actually useless in this context. In this paper we examine this paradox and propose a simple procedure that reconciles the strong intuition that a known propensity functions should be useful for estimating treatment effects with the previous literature suggesting otherwise. Further, simulation studies suggest that direct regression may be preferable to inverse-propensity weight estimators in many circumstances.