Generative Bayesian Hyperparameter Tuning

\noindent Hyper-parameter selection is a central practical problem in modern machine learning, governing regularization strength, model capacity, and robustness choices. Cross-validation is often computationally prohibitive at scale, while fully Bayesian hyper-parameter learning can be difficult due to the cost of posterior sampling. We develop a generative perspective on hyper-parameter tuning that combines two ideas: (i) optimization-based approximations to Bayesian posteriors via randomized, weighted objectives (weighted Bayesian bootstrap), and (ii) amortization of repeated optimization across many hyper-parameter settings by learning a transport map from hyper-parameters (including random weights) to the corresponding optimizer. This yields a ``generator look-up table'' for estimators, enabling rapid evaluation over grids or continuous ranges of hyper-parameters and supporting both predictive tuning objectives and approximate Bayesian uncertainty quantification. We connect this viewpoint to weighted $M$-estimation, envelope/auxiliary-variable representations that reduce non-quadratic losses to weighted least squares, and recent generative samplers for weighted $M$-estimators.

Bayesian Double Descent

Double descent is a phenomenon of over-parameterized statistical models. Our goal is to view double descent from a Bayesian perspective. Over-parameterized models such as deep neural networks have an interesting re-descending property in their risk characteristics. This is a recent phenomenon in machine learning and has been the subject of many studies. As the complexity of the model increases, there is a U-shaped region corresponding to the traditional bias-variance trade-off, but then as the number of parameters equals the number of observations and the model becomes one of interpolation, the risk can become infinite and then, in the over-parameterized region, it re-descends -- the double descent effect. We show that this has a natural Bayesian interpretation. Moreover, we show that it is not in conflict with the traditional Occam's razor that Bayesian models possess, in that they tend to prefer simpler models when possible. We illustrate the approach with an example of Bayesian model selection in neural networks. Finally, we conclude with directions for future research.

Generative Bayesian Computation for Maximum Expected Utility

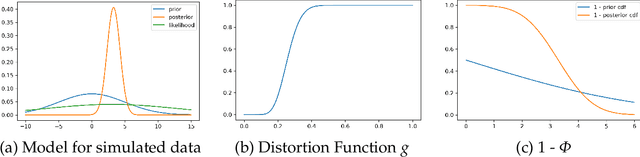
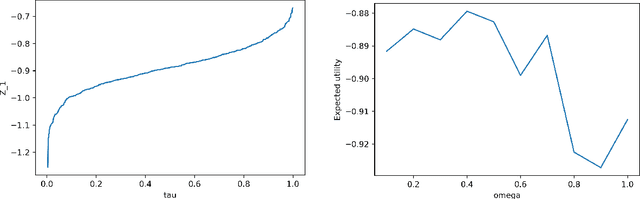
Generative Bayesian Computation (GBC) methods are developed to provide an efficient computational solution for maximum expected utility (MEU). We propose a density-free generative method based on quantiles that naturally calculates expected utility as a marginal of quantiles. Our approach uses a deep quantile neural estimator to directly estimate distributional utilities. Generative methods assume only the ability to simulate from the model and parameters and as such are likelihood-free. A large training dataset is generated from parameters and output together with a base distribution. Our method a number of computational advantages primarily being density-free with an efficient estimator of expected utility. A link with the dual theory of expected utility and risk taking is also discussed. To illustrate our methodology, we solve an optimal portfolio allocation problem with Bayesian learning and a power utility (a.k.a. fractional Kelly criterion). Finally, we conclude with directions for future research.

Deep Learning: A Tutorial

Our goal is to provide a review of deep learning methods which provide insight into structured high-dimensional data. Rather than using shallow additive architectures common to most statistical models, deep learning uses layers of semi-affine input transformations to provide a predictive rule. Applying these layers of transformations leads to a set of attributes (or, features) to which probabilistic statistical methods can be applied. Thus, the best of both worlds can be achieved: scalable prediction rules fortified with uncertainty quantification, where sparse regularization finds the features.

Quantum Bayes AI

Quantum Bayesian AI (Q-B) is an emerging field that levers the computational gains available in Quantum computing. The promise is an exponential speed-up in many Bayesian algorithms. Our goal is to apply these methods directly to statistical and machine learning problems. We provide a duality between classical and quantum probability for calculating of posterior quantities of interest. Our framework unifies MCMC, Deep Learning and Quantum Learning calculations from the viewpoint from von Neumann's principle of quantum measurement. Quantum embeddings and neural gates are also an important part of data encoding and feature selection. There is a natural duality with well-known kernel methods in statistical learning. We illustrate the behaviour of quantum algorithms on two simple classification algorithms. Finally, we conclude with directions for future research.

Merging Two Cultures: Deep and Statistical Learning

Merging the two cultures of deep and statistical learning provides insights into structured high-dimensional data. Traditional statistical modeling is still a dominant strategy for structured tabular data. Deep learning can be viewed through the lens of generalized linear models (GLMs) with composite link functions. Sufficient dimensionality reduction (SDR) and sparsity performs nonlinear feature engineering. We show that prediction, interpolation and uncertainty quantification can be achieved using probabilistic methods at the output layer of the model. Thus a general framework for machine learning arises that first generates nonlinear features (a.k.a factors) via sparse regularization and stochastic gradient optimisation and second uses a stochastic output layer for predictive uncertainty. Rather than using shallow additive architectures as in many statistical models, deep learning uses layers of semi affine input transformations to provide a predictive rule. Applying these layers of transformations leads to a set of attributes (a.k.a features) to which predictive statistical methods can be applied. Thus we achieve the best of both worlds: scalability and fast predictive rule construction together with uncertainty quantification. Sparse regularisation with un-supervised or supervised learning finds the features. We clarify the duality between shallow and wide models such as PCA, PPR, RRR and deep but skinny architectures such as autoencoders, MLPs, CNN, and LSTM. The connection with data transformations is of practical importance for finding good network architectures. By incorporating probabilistic components at the output level we allow for predictive uncertainty. For interpolation we use deep Gaussian process and ReLU trees for classification. We provide applications to regression, classification and interpolation. Finally, we conclude with directions for future research.

Chess AI: Competing Paradigms for Machine Intelligence

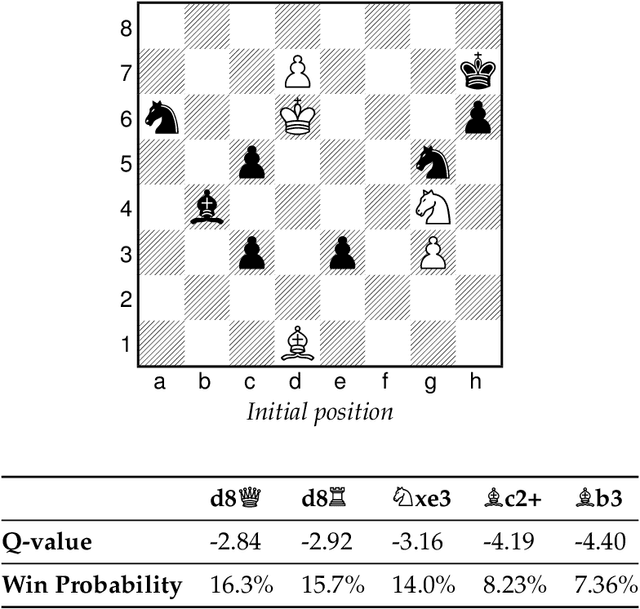
Endgame studies have long served as a tool for testing human creativity and intelligence. We find that they can serve as a tool for testing machine ability as well. Two of the leading chess engines, Stockfish and Leela Chess Zero (LCZero), employ significantly different methods during play. We use Plaskett's Puzzle, a famous endgame study from the late 1970s, to compare the two engines. Our experiments show that Stockfish outperforms LCZero on the puzzle. We examine the algorithmic differences between the engines and use our observations as a basis for carefully interpreting the test results. Drawing inspiration from how humans solve chess problems, we ask whether machines can possess a form of imagination. On the theoretical side, we describe how Bellman's equation may be applied to optimize the probability of winning. To conclude, we discuss the implications of our work on artificial intelligence (AI) and artificial general intelligence (AGI), suggesting possible avenues for future research.

Karpov's Queen Sacrifices and AI

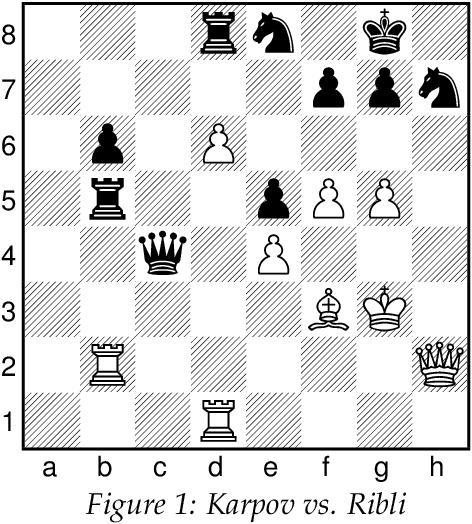
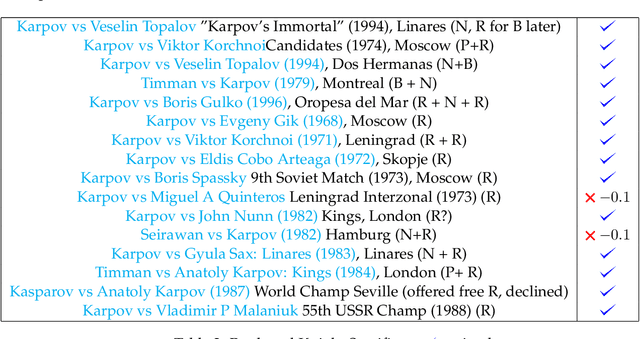
Anatoly Karpov's Queen sacrifices are analyzed. Stockfish 14 NNUE -- an AI chess engine -- evaluates how efficient Karpov's sacrifices are. For comparative purposes, we provide a dataset on Karpov's Rook and Knight sacrifices to test whether Karpov achieves a similar level of accuracy. Our study has implications for human-AI interaction and how humans can better understand the strategies employed by black-box AI algorithms. Finally, we conclude with implications for human study in. chess with computer engines.