GNN-MultiFix: Addressing the pitfalls for GNNs for multi-label node classification

Graph neural networks (GNNs) have emerged as powerful models for learning representations of graph data showing state of the art results in various tasks. Nevertheless, the superiority of these methods is usually supported by either evaluating their performance on small subset of benchmark datasets or by reasoning about their expressive power in terms of certain graph isomorphism tests. In this paper we critically analyse both these aspects through a transductive setting for the task of node classification. First, we delve deeper into the case of multi-label node classification which offers a more realistic scenario and has been ignored in most of the related works. Through analysing the training dynamics for GNN methods we highlight the failure of GNNs to learn over multi-label graph datasets even for the case of abundant training data. Second, we show that specifically for transductive node classification, even the most expressive GNN may fail to learn in absence of node attributes and without using explicit label information as input. To overcome this deficit, we propose a straightforward approach, referred to as GNN-MultiFix, that integrates the feature, label, and positional information of a node. GNN-MultiFix demonstrates significant improvement across all the multi-label datasets. We release our code at https://anonymous.4open.science/r/Graph-MultiFix-4121.

A data-centric approach for assessing progress of Graph Neural Networks

Graph Neural Networks (GNNs) have achieved state-of-the-art results in node classification tasks. However, most improvements are in multi-class classification, with less focus on the cases where each node could have multiple labels. The first challenge in studying multi-label node classification is the scarcity of publicly available datasets. To address this, we collected and released three real-world biological datasets and developed a multi-label graph generator with tunable properties. We also argue that traditional notions of homophily and heterophily do not apply well to multi-label scenarios. Therefore, we define homophily and Cross-Class Neighborhood Similarity for multi-label classification and investigate $9$ collected multi-label datasets. Lastly, we conducted a large-scale comparative study with $8$ methods across nine datasets to evaluate current progress in multi-label node classification. We release our code at \url{https://github.com/Tianqi-py/MLGNC}.

Multi-label Node Classification On Graph-Structured Data

Graph Neural Networks (GNNs) have shown state-of-the-art improvements in node classification tasks on graphs. While these improvements have been largely demonstrated in a multi-class classification scenario, a more general and realistic scenario in which each node could have multiple labels has so far received little attention. The first challenge in conducting focused studies on multi-label node classification is the limited number of publicly available multi-label graph datasets. Therefore, as our first contribution, we collect and release three real-world biological datasets and develop a multi-label graph generator to generate datasets with tunable properties. While high label similarity (high homophily) is usually attributed to the success of GNNs, we argue that a multi-label scenario does not follow the usual semantics of homophily and heterophily so far defined for a multi-class scenario. As our second contribution, besides defining homophily for the multi-label scenario, we develop a new approach that dynamically fuses the feature and label correlation information to learn label-informed representations. Finally, we perform a large-scale comparative study with $10$ methods and $9$ datasets which also showcase the effectiveness of our approach. We release our benchmark at \url{https://anonymous.4open.science/r/LFLF-5D8C/}.

ECG Heartbeat classification using deep transfer learning with Convolutional Neural Network and STFT technique

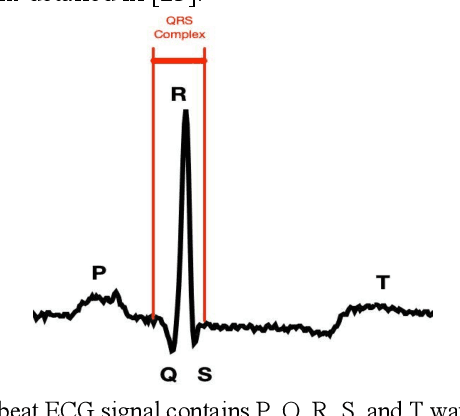
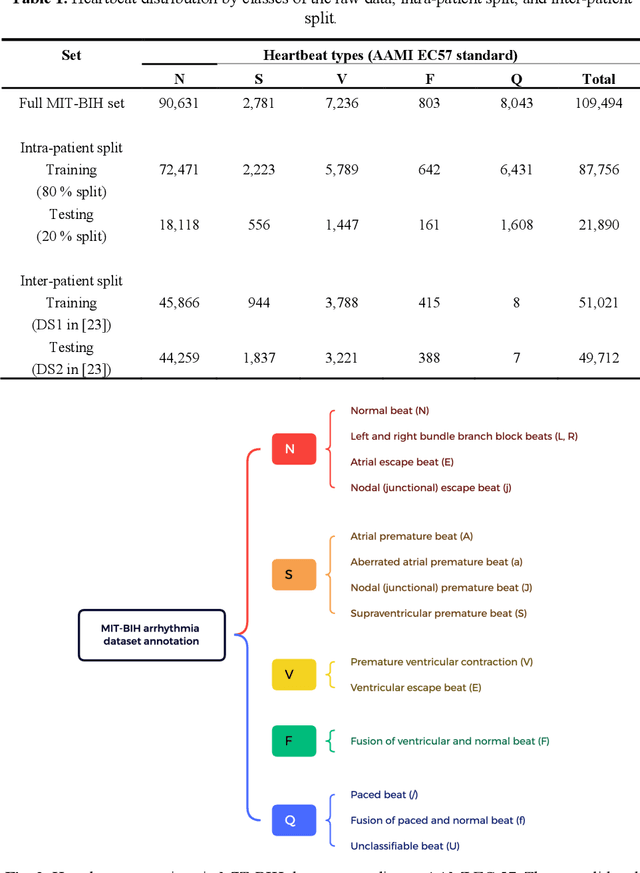
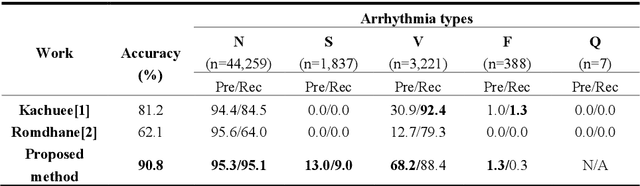
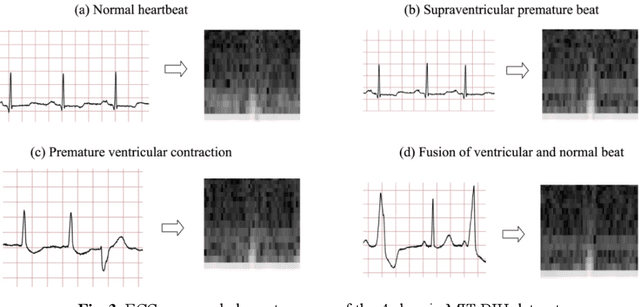
Electrocardiogram (ECG) is a simple non-invasive measure to identify heart-related issues such as irregular heartbeats known as arrhythmias. While artificial intelligence and machine learning is being utilized in a wide range of healthcare related applications and datasets, many arrhythmia classifiers using deep learning methods have been proposed in recent years. However, sizes of the available datasets from which to build and assess machine learning models is often very small and the lack of well-annotated public ECG datasets is evident. In this paper, we propose a deep transfer learning framework that is aimed to perform classification on a small size training dataset. The proposed method is to fine-tune a general-purpose image classifier ResNet-18 with MIT-BIH arrhythmia dataset in accordance with the AAMI EC57 standard. This paper further investigates many existing deep learning models that have failed to avoid data leakage against AAMI recommendations. We compare how different data split methods impact the model performance. This comparison study implies that future work in arrhythmia classification should follow the AAMI EC57 standard when using any including MIT-BIH arrhythmia dataset.

Deep Multimodal Learning: An Effective Method for Video Classification

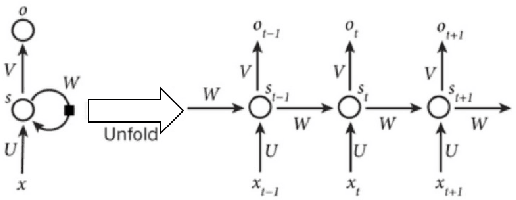
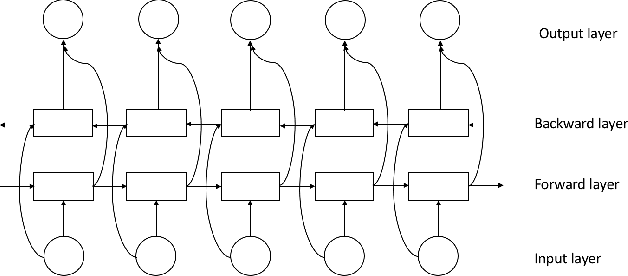
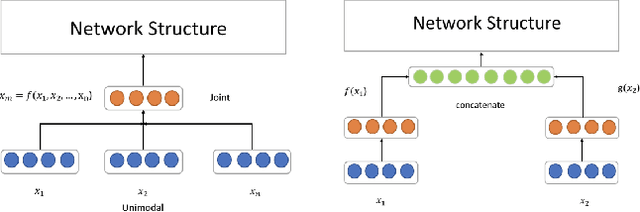
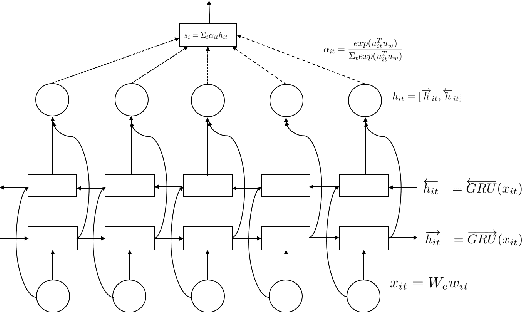
Videos have become ubiquitous on the Internet. And video analysis can provide lots of information for detecting and recognizing objects as well as help people understand human actions and interactions with the real world. However, facing data as huge as TB level, effective methods should be applied. Recurrent neural network (RNN) architecture has wildly been used on many sequential learning problems such as Language Model, Time-Series Analysis, etc. In this paper, we propose some variations of RNN such as stacked bidirectional LSTM/GRU network with attention mechanism to categorize large-scale video data. We also explore different multimodal fusion methods. Our model combines both visual and audio information on both video and frame level and received great result. Ensemble methods are also applied. Because of its multimodal characteristics, we decide to call this method Deep Multimodal Learning(DML). Our DML-based model was trained on Google Cloud and our own server and was tested in a well-known video classification competition on Kaggle held by Google.

Monocular Depth Estimation with Augmented Ordinal Depth Relationships

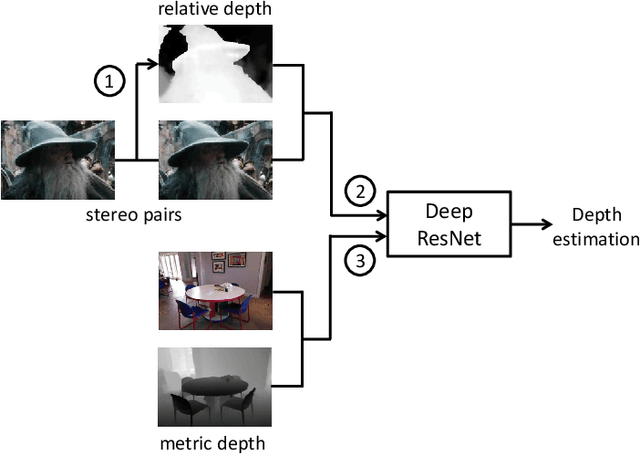
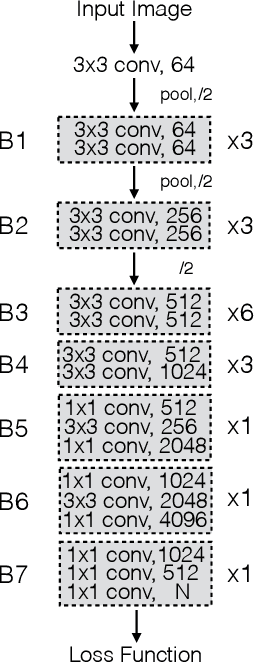
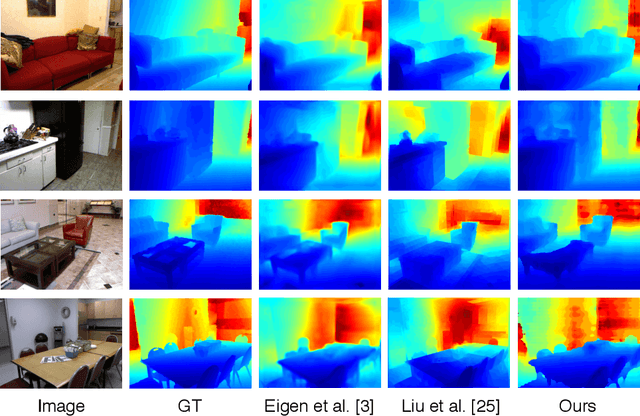
Most existing algorithms for depth estimation from single monocular images need large quantities of metric groundtruth depths for supervised learning. We show that relative depth can be an informative cue for metric depth estimation and can be easily obtained from vast stereo videos. Acquiring metric depths from stereo videos is sometimes impracticable due to the absence of camera parameters. In this paper, we propose to improve the performance of metric depth estimation with relative depths collected from stereo movie videos using existing stereo matching algorithm. We introduce a new "Relative Depth in Stereo" (RDIS) dataset densely labelled with relative depths. We first pretrain a ResNet model on our RDIS dataset. Then we finetune the model on RGB-D datasets with metric ground-truth depths. During our finetuning, we formulate depth estimation as a classification task. This re-formulation scheme enables us to obtain the confidence of a depth prediction in the form of probability distribution. With this confidence, we propose an information gain loss to make use of the predictions that are close to ground-truth. We evaluate our approach on both indoor and outdoor benchmark RGB-D datasets and achieve state-of-the-art performance.

Episodic Memory Deep Q-Networks

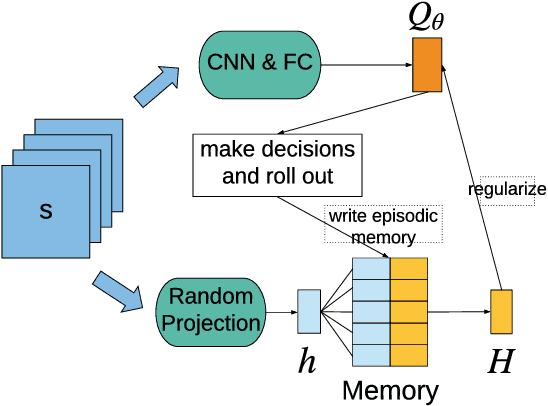
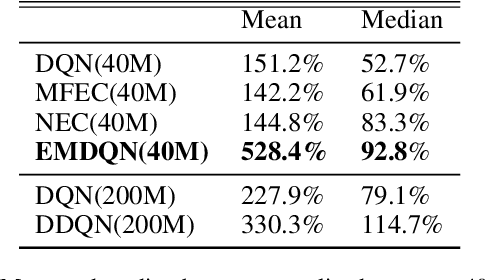
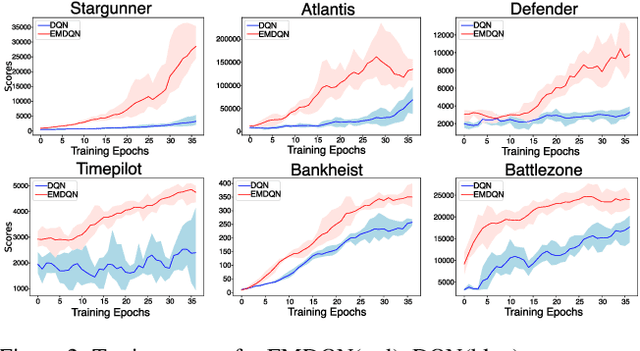
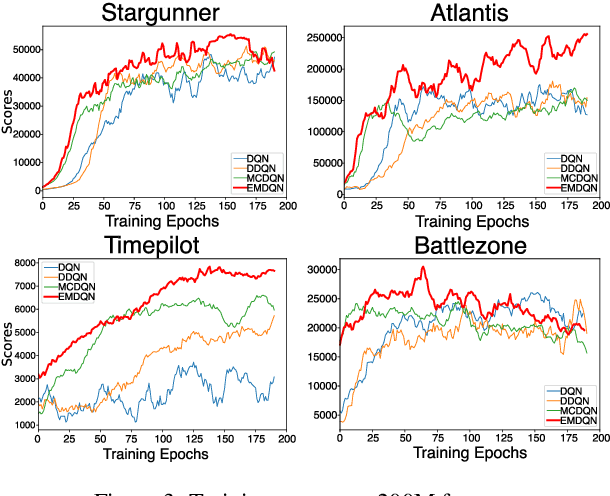
Reinforcement learning (RL) algorithms have made huge progress in recent years by leveraging the power of deep neural networks (DNN). Despite the success, deep RL algorithms are known to be sample inefficient, often requiring many rounds of interaction with the environments to obtain satisfactory performance. Recently, episodic memory based RL has attracted attention due to its ability to latch on good actions quickly. In this paper, we present a simple yet effective biologically inspired RL algorithm called Episodic Memory Deep Q-Networks (EMDQN), which leverages episodic memory to supervise an agent during training. Experiments show that our proposed method can lead to better sample efficiency and is more likely to find good policies. It only requires 1/5 of the interactions of DQN to achieve many state-of-the-art performances on Atari games, significantly outperforming regular DQN and other episodic memory based RL algorithms.

Relative Depth Order Estimation Using Multi-scale Densely Connected Convolutional Networks

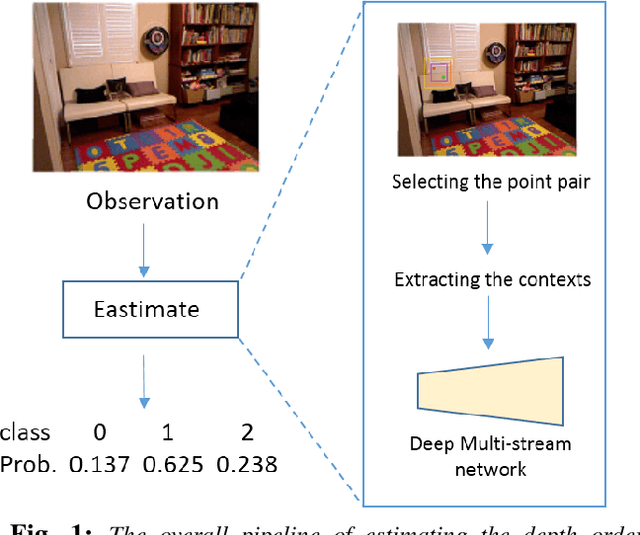
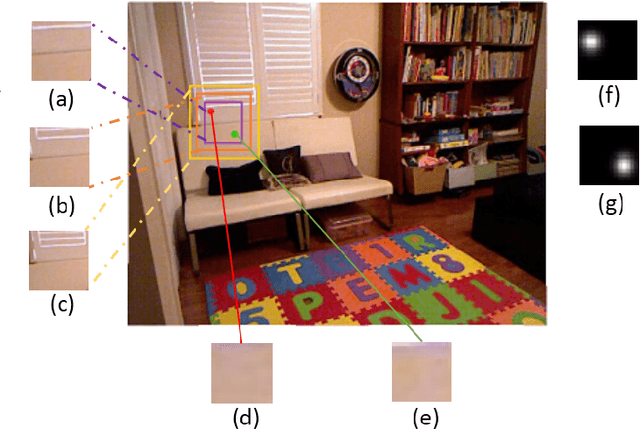
We study the problem of estimating the relative depth order of point pairs in a monocular image. Recent advances mainly focus on using deep convolutional neural networks (DCNNs) to learn and infer the ordinal information from multiple contextual information of the points pair such as global scene context, local contextual information, and the locations. However, it remains unclear how much each context contributes to the task. To address this, we first examine the contribution of each context cue [1], [2] to the performance in the context of depth order estimation. We find out the local context surrounding the points pair contributes the most and the global scene context helps little. Based on the findings, we propose a simple method, using a multi-scale densely-connected network to tackle the task. Instead of learning the global structure, we dedicate to explore the local structure by learning to regress from regions of multiple sizes around the point pairs. Moreover, we use the recent densely connected network [3] to encourage substantial feature reuse as well as deepen our network to boost the performance. We show in experiments that the results of our approach is on par with or better than the state-of-the-art methods with the benefit of using only a small number of training data.

A Likelihood Ratio Framework for High Dimensional Semiparametric Regression

We propose a likelihood ratio based inferential framework for high dimensional semiparametric generalized linear models. This framework addresses a variety of challenging problems in high dimensional data analysis, including incomplete data, selection bias, and heterogeneous multitask learning. Our work has three main contributions. (i) We develop a regularized statistical chromatography approach to infer the parameter of interest under the proposed semiparametric generalized linear model without the need of estimating the unknown base measure function. (ii) We propose a new framework to construct post-regularization confidence regions and tests for the low dimensional components of high dimensional parameters. Unlike existing post-regularization inferential methods, our approach is based on a novel directional likelihood. In particular, the framework naturally handles generic regularized estimators with nonconvex penalty functions and it can be used to infer least false parameters under misspecified models. (iii) We develop new concentration inequalities and normal approximation results for U-statistics with unbounded kernels, which are of independent interest. We demonstrate the consequences of the general theory by using an example of missing data problem. Extensive simulation studies and real data analysis are provided to illustrate our proposed approach.

A General Framework for Robust Testing and Confidence Regions in High-Dimensional Quantile Regression

We propose a robust inferential procedure for assessing uncertainties of parameter estimation in high-dimensional linear models, where the dimension $p$ can grow exponentially fast with the sample size $n$. Our method combines the de-biasing technique with the composite quantile function to construct an estimator that is asymptotically normal. Hence it can be used to construct valid confidence intervals and conduct hypothesis tests. Our estimator is robust and does not require the existence of first or second moment of the noise distribution. It also preserves efficiency in the sense that the worst case efficiency loss is less than 30\% compared to the square-loss-based de-biased Lasso estimator. In many cases our estimator is close to or better than the latter, especially when the noise is heavy-tailed. Our de-biasing procedure does not require solving the $L_1$-penalized composite quantile regression. Instead, it allows for any first-stage estimator with desired convergence rate and empirical sparsity. The paper also provides new proof techniques for developing theoretical guarantees of inferential procedures with non-smooth loss functions. To establish the main results, we exploit the local curvature of the conditional expectation of composite quantile loss and apply empirical process theories to control the difference between empirical quantities and their conditional expectations. Our results are established under weaker assumptions compared to existing work on inference for high-dimensional quantile regression. Furthermore, we consider a high-dimensional simultaneous test for the regression parameters by applying the Gaussian approximation and multiplier bootstrap theories. We also study distributed learning and exploit the divide-and-conquer estimator to reduce computation complexity when the sample size is massive. Finally, we provide empirical results to verify the theory.