A Likelihood Ratio Framework for High Dimensional Semiparametric Regression
Paper and Code
Nov 23, 2015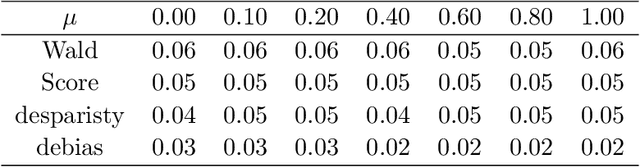
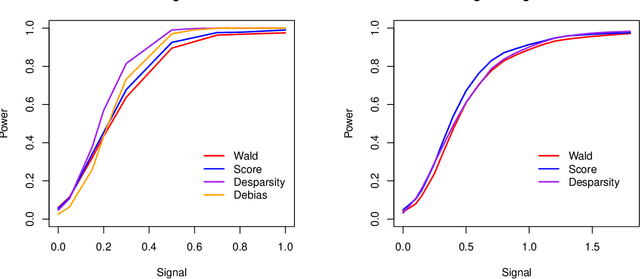
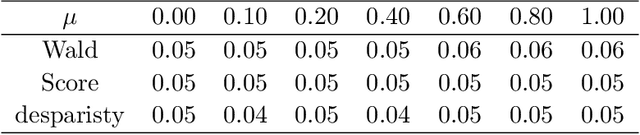
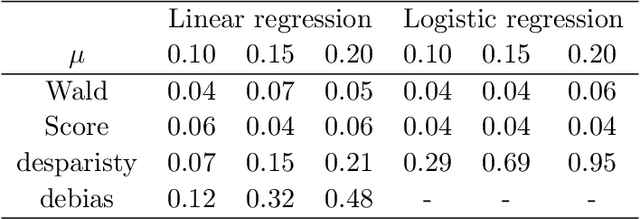
We propose a likelihood ratio based inferential framework for high dimensional semiparametric generalized linear models. This framework addresses a variety of challenging problems in high dimensional data analysis, including incomplete data, selection bias, and heterogeneous multitask learning. Our work has three main contributions. (i) We develop a regularized statistical chromatography approach to infer the parameter of interest under the proposed semiparametric generalized linear model without the need of estimating the unknown base measure function. (ii) We propose a new framework to construct post-regularization confidence regions and tests for the low dimensional components of high dimensional parameters. Unlike existing post-regularization inferential methods, our approach is based on a novel directional likelihood. In particular, the framework naturally handles generic regularized estimators with nonconvex penalty functions and it can be used to infer least false parameters under misspecified models. (iii) We develop new concentration inequalities and normal approximation results for U-statistics with unbounded kernels, which are of independent interest. We demonstrate the consequences of the general theory by using an example of missing data problem. Extensive simulation studies and real data analysis are provided to illustrate our proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge