A General Framework for Robust Testing and Confidence Regions in High-Dimensional Quantile Regression
Paper and Code
Mar 18, 2015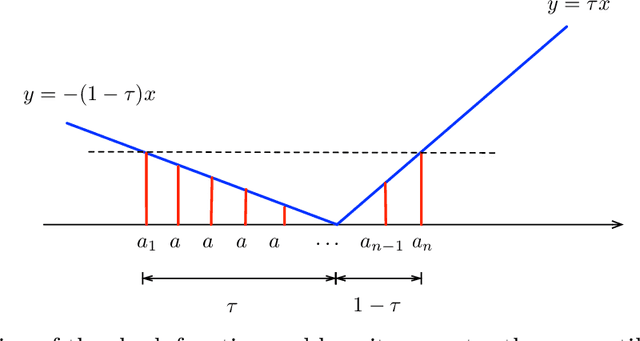
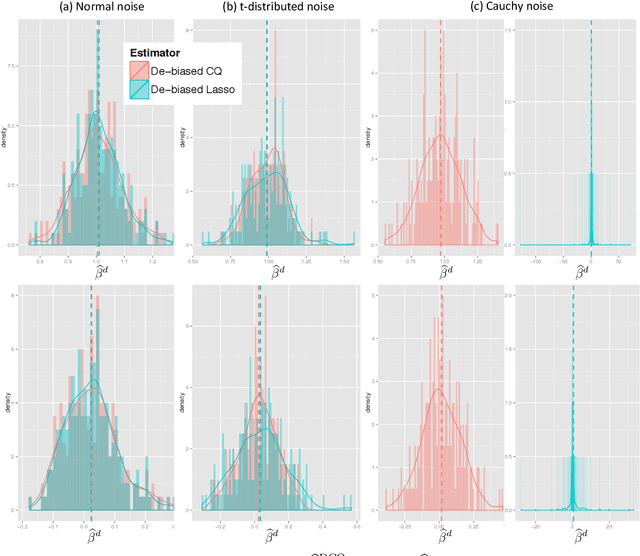
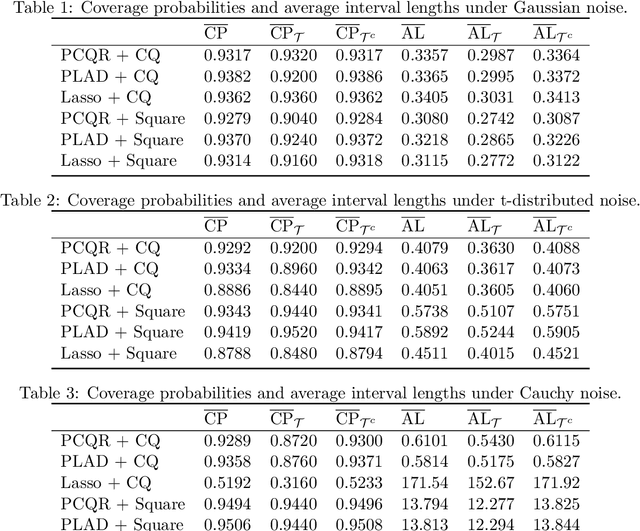
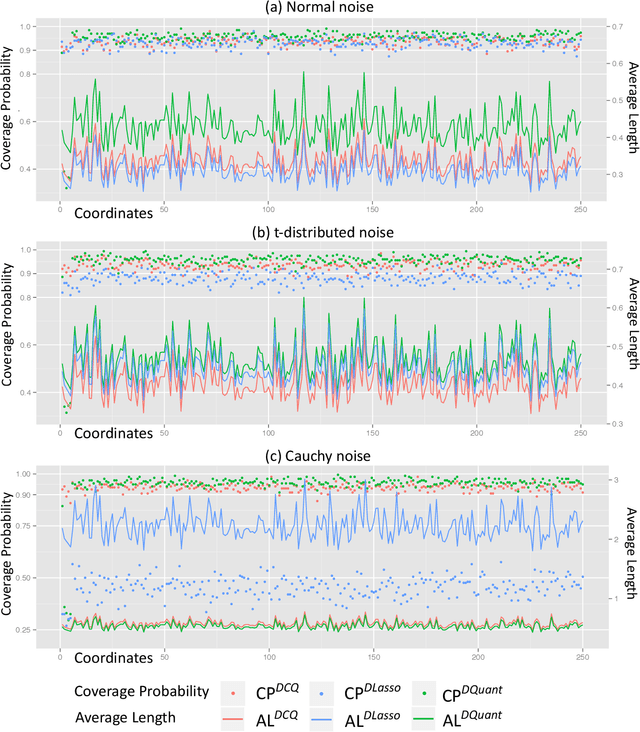
We propose a robust inferential procedure for assessing uncertainties of parameter estimation in high-dimensional linear models, where the dimension $p$ can grow exponentially fast with the sample size $n$. Our method combines the de-biasing technique with the composite quantile function to construct an estimator that is asymptotically normal. Hence it can be used to construct valid confidence intervals and conduct hypothesis tests. Our estimator is robust and does not require the existence of first or second moment of the noise distribution. It also preserves efficiency in the sense that the worst case efficiency loss is less than 30\% compared to the square-loss-based de-biased Lasso estimator. In many cases our estimator is close to or better than the latter, especially when the noise is heavy-tailed. Our de-biasing procedure does not require solving the $L_1$-penalized composite quantile regression. Instead, it allows for any first-stage estimator with desired convergence rate and empirical sparsity. The paper also provides new proof techniques for developing theoretical guarantees of inferential procedures with non-smooth loss functions. To establish the main results, we exploit the local curvature of the conditional expectation of composite quantile loss and apply empirical process theories to control the difference between empirical quantities and their conditional expectations. Our results are established under weaker assumptions compared to existing work on inference for high-dimensional quantile regression. Furthermore, we consider a high-dimensional simultaneous test for the regression parameters by applying the Gaussian approximation and multiplier bootstrap theories. We also study distributed learning and exploit the divide-and-conquer estimator to reduce computation complexity when the sample size is massive. Finally, we provide empirical results to verify the theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge